Water in contact with air actually possesses a finite surface tension,
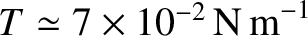 (Haynes and Lide 2011b), which allows there to be a small pressure discontinuity
across a free surface that is curved. In fact,
(Haynes and Lide 2011b), which allows there to be a small pressure discontinuity
across a free surface that is curved. In fact,
![$\displaystyle [p]_{z=0_-}^{z=0_+} = T\,\frac{\partial^{\,2} \zeta}{\partial x^{\,2}}$](img3160.png) |
(9.325) |
(Batchelor 2000).
Here,
 is the radius of curvature of the surface.
Thus, in the presence of surface tension, the boundary condition (9.276)
takes the modified form
is the radius of curvature of the surface.
Thus, in the presence of surface tension, the boundary condition (9.276)
takes the modified form
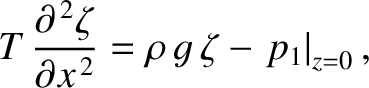 |
(9.326) |
which reduces to
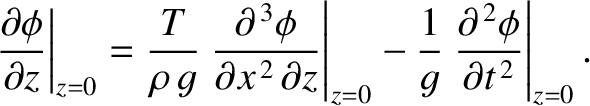 |
(9.327) |
This boundary condition can be combined with the solution (9.281), in the
deep water limit 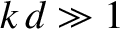 , to give the modified deep water dispersion
relation (see Exercise 26)
, to give the modified deep water dispersion
relation (see Exercise 26)
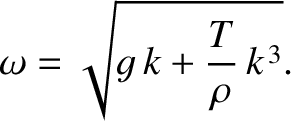 |
(9.328) |
Hence, the phase velocity of the waves takes the form
 |
(9.329) |
and the ratio of the group velocity to the phase velocity can be shown to
be
![$\displaystyle \frac{v_g}{v_p} = \frac{k}{\omega}\,\frac{d\omega}{dk}=\frac{1}{2}\left[\frac{1+3\,T\,k^{\,2}/(\rho\,g)}{1+T\,k^{\,2}/(\rho\,g)}\right].$](img3166.png) |
(9.330) |
We conclude that the phase velocity of surface water waves attains a minimum value of
 when
when
 , which corresponds to
, which corresponds to
 . The group velocity equals the phase velocity at this wavelength. For long wavelength waves (i.e.,
. The group velocity equals the phase velocity at this wavelength. For long wavelength waves (i.e.,
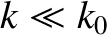 ), gravity dominates surface tension, the phase velocity scales as
), gravity dominates surface tension, the phase velocity scales as
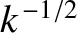 ,
and the group velocity is half the phase velocity. As we have already mentioned, this type of wave is known as a gravity wave.
On the other hand, for
short wavelength waves (i.e.,
,
and the group velocity is half the phase velocity. As we have already mentioned, this type of wave is known as a gravity wave.
On the other hand, for
short wavelength waves (i.e., 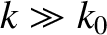 ), surface tension dominates gravity, the
phase velocity scales as
), surface tension dominates gravity, the
phase velocity scales as 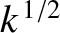 , and the group velocity is
, and the group velocity is  times the
phase velocity. This type of wave is known as a capillary wave.
The fact that the phase velocity and the group velocity both
attain minimum values when
times the
phase velocity. This type of wave is known as a capillary wave.
The fact that the phase velocity and the group velocity both
attain minimum values when
 means that when a
wave disturbance containing a wide spectrum of wavelengths, such as might be
generated by throwing a rock into the water, travels
across the surface of a lake, and reaches the shore, the short and long wavelength components of the disturbance generally arrive before the components of intermediate wavelength.
means that when a
wave disturbance containing a wide spectrum of wavelengths, such as might be
generated by throwing a rock into the water, travels
across the surface of a lake, and reaches the shore, the short and long wavelength components of the disturbance generally arrive before the components of intermediate wavelength.
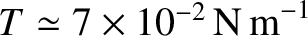 (Haynes and Lide 2011b), which allows there to be a small pressure discontinuity
across a free surface that is curved. In fact,
(Haynes and Lide 2011b), which allows there to be a small pressure discontinuity
across a free surface that is curved. In fact,
![$\displaystyle [p]_{z=0_-}^{z=0_+} = T\,\frac{\partial^{\,2} \zeta}{\partial x^{\,2}}$](img3160.png)
 is the radius of curvature of the surface.
Thus, in the presence of surface tension, the boundary condition (9.276)
takes the modified form
is the radius of curvature of the surface.
Thus, in the presence of surface tension, the boundary condition (9.276)
takes the modified form
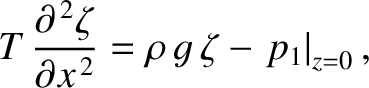
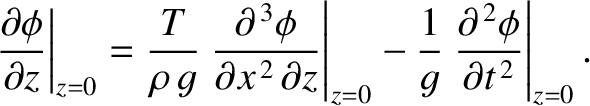
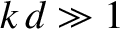 , to give the modified deep water dispersion
relation (see Exercise 26)
Hence, the phase velocity of the waves takes the form
, to give the modified deep water dispersion
relation (see Exercise 26)
Hence, the phase velocity of the waves takes the form

![$\displaystyle \frac{v_g}{v_p} = \frac{k}{\omega}\,\frac{d\omega}{dk}=\frac{1}{2}\left[\frac{1+3\,T\,k^{\,2}/(\rho\,g)}{1+T\,k^{\,2}/(\rho\,g)}\right].$](img3166.png)
 when
when
 , which corresponds to
, which corresponds to
 . The group velocity equals the phase velocity at this wavelength. For long wavelength waves (i.e.,
. The group velocity equals the phase velocity at this wavelength. For long wavelength waves (i.e.,
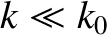 ), gravity dominates surface tension, the phase velocity scales as
), gravity dominates surface tension, the phase velocity scales as
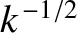 ,
and the group velocity is half the phase velocity. As we have already mentioned, this type of wave is known as a gravity wave.
On the other hand, for
short wavelength waves (i.e.,
,
and the group velocity is half the phase velocity. As we have already mentioned, this type of wave is known as a gravity wave.
On the other hand, for
short wavelength waves (i.e., 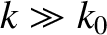 ), surface tension dominates gravity, the
phase velocity scales as
), surface tension dominates gravity, the
phase velocity scales as 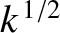 , and the group velocity is
, and the group velocity is  times the
phase velocity. This type of wave is known as a capillary wave.
The fact that the phase velocity and the group velocity both
attain minimum values when
times the
phase velocity. This type of wave is known as a capillary wave.
The fact that the phase velocity and the group velocity both
attain minimum values when
 means that when a
wave disturbance containing a wide spectrum of wavelengths, such as might be
generated by throwing a rock into the water, travels
across the surface of a lake, and reaches the shore, the short and long wavelength components of the disturbance generally arrive before the components of intermediate wavelength.
means that when a
wave disturbance containing a wide spectrum of wavelengths, such as might be
generated by throwing a rock into the water, travels
across the surface of a lake, and reaches the shore, the short and long wavelength components of the disturbance generally arrive before the components of intermediate wavelength.