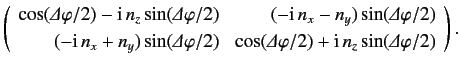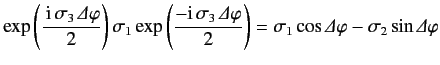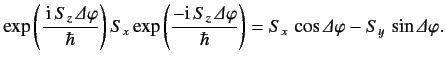Next: Spin Greater Than One-Half
Up: Spin Angular Momentum
Previous: Spin Precession
Pauli Two-Component Formalism
We have seen, in Section 4.4, that the eigenstates of orbital angular momentum
can be conveniently represented as spherical harmonics. In this
representation, the orbital angular momentum
operators take the form of differential operators involving only
angular coordinates. It is conventional to represent the eigenstates of spin
angular momentum as column (or row) matrices. In this representation,
the spin angular momentum operators take the form of matrices.
The matrix representation of a spin one-half system was introduced by Pauli in 1926.
Recall, from Section 5.4, that a general spin ket can be expressed as
a linear combination of the two eigenkets of 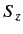 belonging to the
eigenvalues
belonging to the
eigenvalues
 . These are denoted
. These are denoted
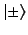 . Let us
represent these basis eigenkets as column vectors:
. Let us
represent these basis eigenkets as column vectors:
The corresponding eigenbras are represented as row vectors:
In this scheme, a general ket takes the form
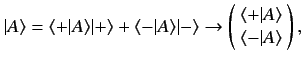 |
(476) |
and a general bra becomes
 |
(477) |
The column vector (476) is called a two-component spinor, and can be written
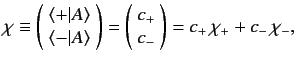 |
(478) |
where the 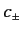 are complex numbers. The row vector (477) becomes
are complex numbers. The row vector (477) becomes
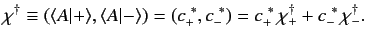 |
(479) |
Consider the ket obtained by the action of a spin operator on
ket  :
:
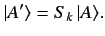 |
(480) |
This ket is represented as
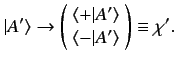 |
(481) |
However,
or
![$\displaystyle \left(\!\begin{array}{c}\langle +\vert A'\rangle\\ [0.5ex] \langl...
...}\langle +\vert A\rangle\\ [0.5ex] \langle -\vert A\rangle\end{array}\!\right).$](img1161.png) |
(484) |
It follows that we can represent the operator/ket relation
(480) as the matrix relation
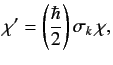 |
(485) |
where the 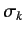 are the matrices of the
are the matrices of the
 values divided by
values divided by 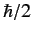 . These matrices, which are called the
Pauli matrices, can easily be evaluated using the explicit forms for the
spin operators given in Equations (427)-(429). We find that
. These matrices, which are called the
Pauli matrices, can easily be evaluated using the explicit forms for the
spin operators given in Equations (427)-(429). We find that
Here, 1, 2, and 3 refer to  ,
, 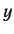 , and
, and  , respectively. Note that, in this
scheme, we are effectively representing the spin operators in terms
of the Pauli matrices:
, respectively. Note that, in this
scheme, we are effectively representing the spin operators in terms
of the Pauli matrices:
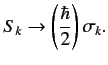 |
(489) |
The expectation value of 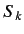 can be written in terms of spinors
and the Pauli matrices:
can be written in terms of spinors
and the Pauli matrices:
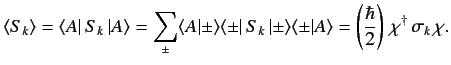 |
(490) |
The fundamental commutation relation for angular momentum, Equation (417), can
be combined with (489) to give the following commutation relation
for the Pauli matrices:
It is easily seen that the matrices (486)-(488) actually satisfy these relations
(i.e.,
 , plus
all cyclic permutations). It is also easily seen that the Pauli matrices
satisfy the anti-commutation relations
, plus
all cyclic permutations). It is also easily seen that the Pauli matrices
satisfy the anti-commutation relations
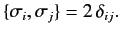 |
(492) |
Here,
 .
.
Let us examine how the Pauli scheme can be extended to take into account the
position of a spin one-half particle. Recall, from Section 5.3,
that we can represent a general basis ket as the product
of basis kets in position space and spin space:
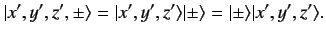 |
(493) |
The ket corresponding to state  is denoted
is denoted
 , and resides
in the product space of the position and spin ket spaces. State
, and resides
in the product space of the position and spin ket spaces. State  is completely
specified by the two wavefunctions
is completely
specified by the two wavefunctions
Consider the operator relation
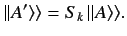 |
(496) |
It is easily seen that
where use has been made of the fact that the spin operator 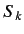 commutes with the
eigenbras
commutes with the
eigenbras
 .
It is fairly obvious that we can represent the operator relation (496) as a matrix relation
if we generalize our definition of a spinor by writing
.
It is fairly obvious that we can represent the operator relation (496) as a matrix relation
if we generalize our definition of a spinor by writing
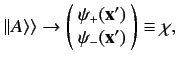 |
(499) |
and so on. The components of a spinor are now wavefunctions, instead of
complex numbers. In this scheme, the operator equation (496) becomes simply
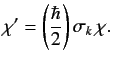 |
(500) |
Consider the operator relation
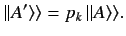 |
(501) |
In the Schrödinger representation, we have
where use has been made of Equation (169). The above equation reduces to
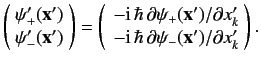 |
(504) |
Thus, the operator equation (501)
can be written
 |
(505) |
where
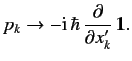 |
(506) |
Here, 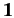 is the
is the 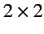 unit matrix. In fact, any position operator
(e.g.,
unit matrix. In fact, any position operator
(e.g., 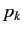 or
or 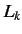 ) is represented in the Pauli scheme as some differential
operator of the position eigenvalues multiplied by the
) is represented in the Pauli scheme as some differential
operator of the position eigenvalues multiplied by the 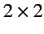 unit matrix.
unit matrix.
What about combinations of position and spin operators? The most
commonly occurring combination is a dot product: e.g.,
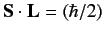
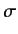
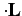 .
Consider the hybrid
operator
.
Consider the hybrid
operator
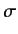
 , where
, where
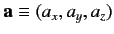 is
some vector position operator. This quantity is represented as
a
is
some vector position operator. This quantity is represented as
a 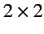 matrix:
matrix:
 ![$\displaystyle \cdot {\bf a} \equiv \sum_k a_k \,\sigma_k = \left(\!\begin{array...
...3 & a_1 -{\rm i}\,a_2\\ [0.5ex] a_1 + {\rm i}\,a_2 & -a_3 \end{array}\!\right).$](img1203.png) |
(507) |
Since, in the Schrödinger representation, a general position operator takes
the form of a differential operator in  ,
,  , or
, or 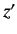 , it is clear that
the above quantity must be regarded as a matrix differential operator that
acts on spinors of the general form (499).
The important identity
, it is clear that
the above quantity must be regarded as a matrix differential operator that
acts on spinors of the general form (499).
The important identity
follows from the commutation and anti-commutation relations (491) and (492). Thus,
A general rotation operator in spin space is written
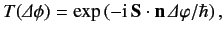 |
(510) |
by analogy with Equation (440), where 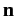 is a unit vector pointing along
the axis of rotation, and
is a unit vector pointing along
the axis of rotation, and
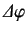 is the angle of rotation.
Here,
is the angle of rotation.
Here, 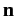 can be regarded as a trivial position operator. The
rotation operator is represented
can be regarded as a trivial position operator. The
rotation operator is represented
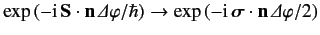 |
(511) |
in the Pauli scheme.
The term on the right-hand side of the above expression is the exponential
of a matrix. This can easily be evaluated using the Taylor series for an exponential,
plus the rules
These rules follow trivially from the identity (508). Thus, we can write
The explicit  form of this matrix is
form of this matrix is
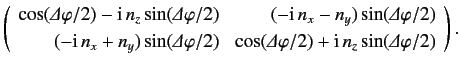 |
(515) |
Rotation matrices act on spinors in much the same manner as the corresponding
rotation operators act on state kets. Thus,
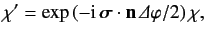 |
(516) |
where 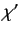 denotes the spinor obtained after rotating the spinor
denotes the spinor obtained after rotating the spinor
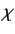 an angle
an angle
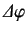 about the
about the 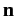 -axis.
The Pauli matrices remain unchanged under rotations.
However, the quantity
-axis.
The Pauli matrices remain unchanged under rotations.
However, the quantity
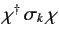 is proportional to the expectation
value of
is proportional to the expectation
value of 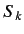 [see Equation (490)], so we would expect it to transform like a
vector under rotation (see Section 5.4). In fact, we
require
[see Equation (490)], so we would expect it to transform like a
vector under rotation (see Section 5.4). In fact, we
require
 |
(517) |
where the 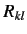 are the elements of a conventional rotation matrix. This
is easily demonstrated, because
are the elements of a conventional rotation matrix. This
is easily demonstrated, because
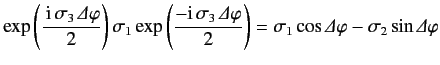 |
(518) |
plus all cyclic permutations. The above expression is the  matrix analogue
of (see Section 5.4)
matrix analogue
of (see Section 5.4)
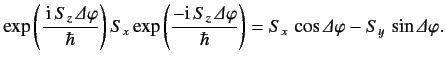 |
(519) |
The previous two formulae can both be validated using the Baker-Hausdorff lemma,
(447), which holds for Hermitian matrices, in addition to Hermitian operators.



Next: Spin Greater Than One-Half
Up: Spin Angular Momentum
Previous: Spin Precession
Richard Fitzpatrick
2013-04-08
![]() belonging to the
eigenvalues
belonging to the
eigenvalues
![]() . These are denoted
. These are denoted
![]() . Let us
represent these basis eigenkets as column vectors:
. Let us
represent these basis eigenkets as column vectors:
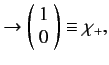

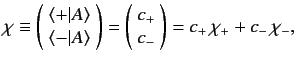
![]() :
:
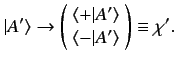
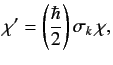
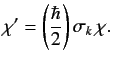
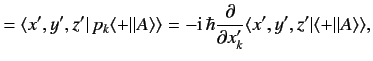
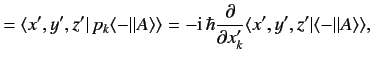
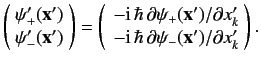
![]()
![]()
![]() .
Consider the hybrid
operator
.
Consider the hybrid
operator
![]()
![]() , where
, where
![]() is
some vector position operator. This quantity is represented as
a
is
some vector position operator. This quantity is represented as
a ![]() matrix:
matrix:
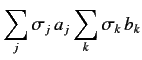
![$\displaystyle = \sum_j \sum_k \left(\frac{1}{2}\, \{\sigma_j, \sigma_k\} + \frac{1}{2} [\sigma_j, \sigma_k]\right) a_j \,b_k$](img1209.png)
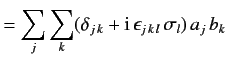
![$\displaystyle = \left[ 1 - \frac{(\mbox{\boldmath$\sigma$}\cdot {\bf n})^2}{2!}...
...t {\bf n})^4}{4!} \left(\frac{{\mit\Delta}\varphi}{2} \right)^4 + \cdots\right]$](img1224.png)
![$\displaystyle - {\rm i} \left[ (\mbox{\boldmath$\sigma$}\cdot {\bf n} )\left( \...
...ot {\bf n})^3}{3!} \left(\frac{{\mit\Delta}\varphi}{2}\right)^3 + \cdots\right]$](img1225.png)