


Next: Wavefunction of Spin One-Half
Up: Spin Angular Momentum
Previous: Introduction
Let us denote the three components of the spin angular momentum of a
particle by the Hermitian operators
 . We assume that these
operators obey the fundamental commutation relations (297)-(299) for the components
of an angular momentum. Thus, we can write
. We assume that these
operators obey the fundamental commutation relations (297)-(299) for the components
of an angular momentum. Thus, we can write
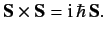 |
(417) |
We can also define the operator
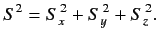 |
(418) |
According to the quite general analysis of Section 4.1,
![$\displaystyle [{\bf S}, S^2] = 0.$](img1016.png) |
(419) |
Thus, it is possible to find simultaneous eigenstates of 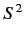 and
and 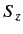 .
These are denoted
.
These are denoted
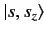 , where
, where
According to the equally general
analysis of Section 4.2, the quantum number 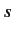 can, in principle,
take integer or half-integer values,
and the quantum number
can, in principle,
take integer or half-integer values,
and the quantum number  can only take the values
can only take the values
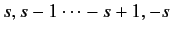 .
.
Spin angular momentum clearly has many properties in common with
orbital angular momentum. However, there is one vitally important difference.
Spin angular momentum operators cannot be expressed in terms of
position and momentum operators, like in Equations (290)-(292), because this
identification depends on an analogy with classical mechanics, and the concept
of spin is purely quantum mechanical: i.e., it has no analogy in classical physics.
Consequently, the restriction that the quantum number of the overall angular
momentum must take integer values is lifted for spin angular momentum,
since this restriction (found in Sections 4.3 and 4.4) depends on Equations (290)-(292).
In other words, the spin quantum number 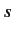 is allowed to take half-integer values.
is allowed to take half-integer values.
Consider a spin one-half particle, for which
Here, the
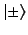 denote eigenkets of the
denote eigenkets of the 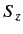 operator corresponding to
the eigenvalues
operator corresponding to
the eigenvalues
 . These kets are mutually orthogonal (since
. These kets are mutually orthogonal (since 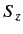 is
an Hermitian operator), so
is
an Hermitian operator), so
 |
(424) |
They are also properly normalized and complete, so that
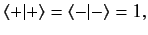 |
(425) |
and
 |
(426) |
It is easily verified that the Hermitian operators defined by
satisfy the commutation relations (297)-(299) (with the 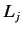 replaced by the
replaced by the  ).
The operator
).
The operator 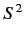 takes the form
takes the form
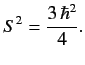 |
(430) |
It is also easily demonstrated that 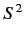 and
and 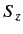 ,
defined in this manner, satisfy the eigenvalue
relations (422)-(423). Equations (427)-(430) constitute a realization
of the spin operators
,
defined in this manner, satisfy the eigenvalue
relations (422)-(423). Equations (427)-(430) constitute a realization
of the spin operators 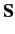 and
and 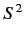 (for a spin one-half particle)
in spin space (i.e., the Hilbert sub-space consisting of kets which
correspond to the different spin states of the particle).
(for a spin one-half particle)
in spin space (i.e., the Hilbert sub-space consisting of kets which
correspond to the different spin states of the particle).



Next: Wavefunction of Spin One-Half
Up: Spin Angular Momentum
Previous: Introduction
Richard Fitzpatrick
2013-04-08
![]() is allowed to take half-integer values.
is allowed to take half-integer values.