


Next: Rotation Operators
Up: Orbital Angular Momentum
Previous: Orbital Angular Momentum
Eigenvalues of Orbital Angular Momentum
Suppose that the simultaneous eigenkets of 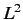 and
and 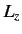 are completely
specified by two quantum numbers,
are completely
specified by two quantum numbers,  and
and  . These kets are denoted
. These kets are denoted
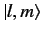 . The quantum number
. The quantum number  is defined by
is defined by
 |
(314) |
Thus,  is the eigenvalue of
is the eigenvalue of 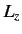 divided by
divided by 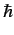 . It is possible
to write such an equation because
. It is possible
to write such an equation because 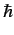 has the dimensions of angular momentum.
Note that
has the dimensions of angular momentum.
Note that  is a real number, because
is a real number, because 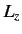 is an Hermitian operator.
is an Hermitian operator.
We can write
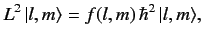 |
(315) |
without loss of generality,
where 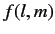 is some real dimensionless function of
is some real dimensionless function of  and
and  . Later on,
we will show that
. Later on,
we will show that
 .
Now,
.
Now,
![$\displaystyle \langle l, m \vert\, L^2 - L_z^{\,2}\, \vert l, m\rangle =\langle...
...(l, m) \,\hbar^2 - m^2\, \hbar^2\, \vert l, m\rangle =[f(l,m) - m^2] \,\hbar^2,$](img786.png) |
(316) |
assuming that the
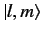 have unit norms. However,
have unit norms. However,
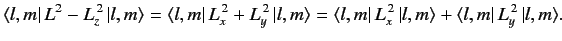 |
(317) |
It is easily demonstrated that
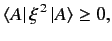 |
(318) |
where  is a general ket, and
is a general ket, and  is an Hermitian operator.
The proof follows from the observation that
is an Hermitian operator.
The proof follows from the observation that
 |
(319) |
where
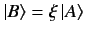 , plus the fact that
, plus the fact that
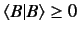 for a general ket
for a general ket 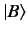 [see Equation (21)]. It follows from
Equations (316)-(318) that
[see Equation (21)]. It follows from
Equations (316)-(318) that
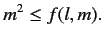 |
(320) |
Consider the effect of the shift operator 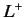 on the eigenket
on the eigenket
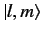 .
It is easily demonstrated that
.
It is easily demonstrated that
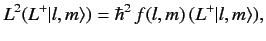 |
(321) |
where use has been made of Equation (315), plus
the fact that 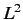 and
and 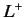 commute.
It follows that the ket
commute.
It follows that the ket
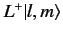 has the same
eigenvalue of
has the same
eigenvalue of 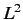 as the ket
as the ket
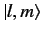 . Thus, the shift operator
. Thus, the shift operator
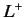 does not affect the magnitude of the angular momentum of
any eigenket it acts upon. However,
does not affect the magnitude of the angular momentum of
any eigenket it acts upon. However,
![$\displaystyle L_z \,L^+ \vert l, m\rangle = (L^+ L_z + [L_z, L^+])\,\vert l,m\r...
...^+ L_z + \hbar\, L^+) \,\vert l,m\rangle = (m+1)\,\hbar \,L^+\vert l, m\rangle,$](img795.png) |
(322) |
where use has been made of Equation (311). The above equation implies
that
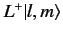 is proportional to
is proportional to
 . We can
write
. We can
write
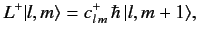 |
(323) |
where
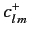 is a number. It is clear that if the operator
is a number. It is clear that if the operator 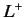 acts on a simultaneous eigenstate of
acts on a simultaneous eigenstate of 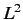 and
and 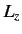 then
the eigenvalue of
then
the eigenvalue of 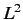 remains unchanged, but the eigenvalue
of
remains unchanged, but the eigenvalue
of 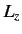 is increased by
is increased by 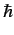 . For this reason,
. For this reason, 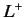 is called
a raising operator.
is called
a raising operator.
Using similar arguments to those given above, it is possible
to demonstrate that
 |
(324) |
Hence, 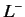 is called a lowering operator.
is called a lowering operator.
The shift operators, 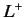 and
and 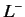 , respectively step the value of
, respectively step the value of  up and down by unity
each time they operate on one of the simultaneous eigenkets of
up and down by unity
each time they operate on one of the simultaneous eigenkets of
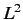 and
and 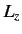 . It would appear, at first sight, that any value of
. It would appear, at first sight, that any value of
 can be obtained by applying these operators a sufficient
number of times. However, according to Equation (320), there is
a definite upper bound to the values that
can be obtained by applying these operators a sufficient
number of times. However, according to Equation (320), there is
a definite upper bound to the values that 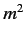 can take. This
bound is determined by the eigenvalue of
can take. This
bound is determined by the eigenvalue of 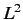 [see Equation (315)]. It follows that there is a maximum and a minimum
possible
value which
[see Equation (315)]. It follows that there is a maximum and a minimum
possible
value which  can take.
Suppose that we attempt to raise the value
of
can take.
Suppose that we attempt to raise the value
of  above its maximum value
above its maximum value
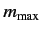 . Since there is no
state with
. Since there is no
state with
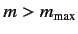 , we must have
, we must have
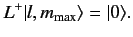 |
(325) |
This implies that
 |
(326) |
However,
![$\displaystyle L^-\, L^+ = L_x^{\,2} + L_y^{\,2} + {\rm i}\,[L_x, L_y] = L^2 - L_z^{\,2} - \hbar \,L_z,$](img805.png) |
(327) |
so Equation (326) yields
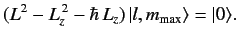 |
(328) |
The above equation can be rearranged to give
 |
(329) |
Comparison of this equation with Equation (315) yields the result
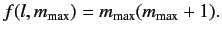 |
(330) |
But, when 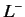 operates on
operates on
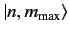 it generates
it generates
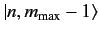 ,
,
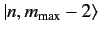 , etc. Since
the lowering operator does not change the eigenvalue of
, etc. Since
the lowering operator does not change the eigenvalue of 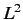 , all of these states
must correspond to the same value of
, all of these states
must correspond to the same value of 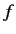 , namely
, namely
 .
Thus,
.
Thus,
 |
(331) |
At this stage, we can give the unknown quantum number  the value
the value
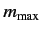 ,
without loss of generality.
We can also write the above equation in the form
,
without loss of generality.
We can also write the above equation in the form
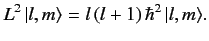 |
(332) |
It is easily seen that
![$\displaystyle L^- \,L^+ \,\vert l, m\rangle = (L^2 - L_z^{\,2}-\hbar\, L_z)\,\vert l, m \rangle = \hbar^2 \,[l\,(l+1) - m\,(m+1)]\,\vert l,m\rangle.$](img815.png) |
(333) |
Thus,
![$\displaystyle \langle l,m\vert\, L^- \,L^+\,\vert l,m\rangle =\hbar^2 \,[l\,(l+1) - m\,(m+1)].$](img816.png) |
(334) |
However, we also know that
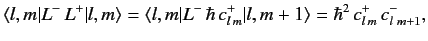 |
(335) |
where use has been made of Equations (323) and (324).
It follows that
![$\displaystyle c^+_{l\,m}\, c^{-}_{l\,\,m+1} = [l\,(l+1) - m\,(m+1)].$](img818.png) |
(336) |
Consider the following:
where use has been made of the fact that 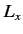 and
and 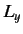 are Hermitian.
The above equation reduces to
are Hermitian.
The above equation reduces to
 |
(338) |
with the aid of Equations (323) and (324).
Equations (336) and (338) can be combined to give
![$\displaystyle \vert c^+_{l\,m}\vert^{\,2} = [l\,(l+1) - m \,(m+1)].$](img825.png) |
(339) |
The solution of the above equation is
 |
(340) |
Note that
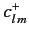 is undetermined to an arbitrary phase-factor
[i.e., we can replace
is undetermined to an arbitrary phase-factor
[i.e., we can replace
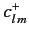 , given above, by
, given above, by
 ,
where
,
where 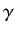 is real, and we still satisfy Equation (339)]. We have made the arbitrary, but convenient, choice that
is real, and we still satisfy Equation (339)]. We have made the arbitrary, but convenient, choice that
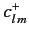 is real and positive. This is equivalent
to choosing the relative phases of the eigenkets
is real and positive. This is equivalent
to choosing the relative phases of the eigenkets
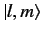 .
According to Equation (338),
.
According to Equation (338),
 |
(341) |
We have already seen that the inequality (320) implies that there is a
maximum and a minimum possible value of  . The maximum value of
. The maximum value of  is denoted
is denoted  . What is the minimum value? Suppose that we try
to lower the value of
. What is the minimum value? Suppose that we try
to lower the value of  below its minimum value
below its minimum value
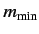 . Because
there is no state with
. Because
there is no state with
 , we must have
, we must have
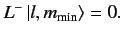 |
(342) |
According to Equation (324), this implies that
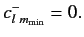 |
(343) |
It can be seen from Equation (341) that
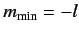 .
We conclude that
.
We conclude that  can take a ``ladder'' of discrete values, each rung differing
from its immediate neighbors by unity. The top rung is
can take a ``ladder'' of discrete values, each rung differing
from its immediate neighbors by unity. The top rung is  , and the
bottom rung is
, and the
bottom rung is 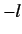 . There are only two possible choices for
. There are only two possible choices for  .
Either it is an integer (e.g.,
.
Either it is an integer (e.g., 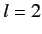 , which allows
, which allows  to take the values
to take the values
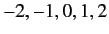 ), or it is a half-integer (e.g.,
), or it is a half-integer (e.g.,  , which allows
, which allows
 to take the values
to take the values
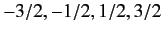 ). We shall prove in the next
section that an orbital angular momentum can only take integer values
of
). We shall prove in the next
section that an orbital angular momentum can only take integer values
of  .
.
In summary, using just the fundamental commutation relations (297)-(299),
plus the fact that 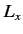 ,
, 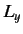 , and
, and 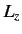 are Hermitian operators, we have
shown that the eigenvalues of
are Hermitian operators, we have
shown that the eigenvalues of
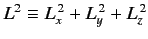 can be written
can be written
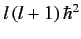 , where
, where  is an integer, or a half-integer.
We have also demonstrated that the eigenvalues of
is an integer, or a half-integer.
We have also demonstrated that the eigenvalues of 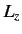 can only
take the values
can only
take the values  , where
, where  lies in the range
lies in the range
 . Let
. Let
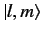 denote a properly normalized simultaneous eigenket
of
denote a properly normalized simultaneous eigenket
of 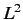 and
and 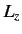 , belonging to the eigenvalues
, belonging to the eigenvalues
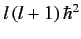 and
and  , respectively.
We have shown that
, respectively.
We have shown that
where
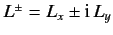 are the so-called shift operators.
are the so-called shift operators.



Next: Rotation Operators
Up: Orbital Angular Momentum
Previous: Orbital Angular Momentum
Richard Fitzpatrick
2013-04-08
![]() on the eigenket
on the eigenket
![]() .
It is easily demonstrated that
.
It is easily demonstrated that
![]() and
and ![]() , respectively step the value of
, respectively step the value of ![]() up and down by unity
each time they operate on one of the simultaneous eigenkets of
up and down by unity
each time they operate on one of the simultaneous eigenkets of
![]() and
and ![]() . It would appear, at first sight, that any value of
. It would appear, at first sight, that any value of
![]() can be obtained by applying these operators a sufficient
number of times. However, according to Equation (320), there is
a definite upper bound to the values that
can be obtained by applying these operators a sufficient
number of times. However, according to Equation (320), there is
a definite upper bound to the values that ![]() can take. This
bound is determined by the eigenvalue of
can take. This
bound is determined by the eigenvalue of ![]() [see Equation (315)]. It follows that there is a maximum and a minimum
possible
value which
[see Equation (315)]. It follows that there is a maximum and a minimum
possible
value which ![]() can take.
Suppose that we attempt to raise the value
of
can take.
Suppose that we attempt to raise the value
of ![]() above its maximum value
above its maximum value
![]() . Since there is no
state with
. Since there is no
state with
![]() , we must have
, we must have
![]() . The maximum value of
. The maximum value of ![]() is denoted
is denoted ![]() . What is the minimum value? Suppose that we try
to lower the value of
. What is the minimum value? Suppose that we try
to lower the value of ![]() below its minimum value
below its minimum value
![]() . Because
there is no state with
. Because
there is no state with
![]() , we must have
, we must have
![]() ,
, ![]() , and
, and ![]() are Hermitian operators, we have
shown that the eigenvalues of
are Hermitian operators, we have
shown that the eigenvalues of
![]() can be written
can be written
![]() , where
, where ![]() is an integer, or a half-integer.
We have also demonstrated that the eigenvalues of
is an integer, or a half-integer.
We have also demonstrated that the eigenvalues of ![]() can only
take the values
can only
take the values ![]() , where
, where ![]() lies in the range
lies in the range
![]() . Let
. Let
![]() denote a properly normalized simultaneous eigenket
of
denote a properly normalized simultaneous eigenket
of ![]() and
and ![]() , belonging to the eigenvalues
, belonging to the eigenvalues
![]() and
and ![]() , respectively.
We have shown that
, respectively.
We have shown that