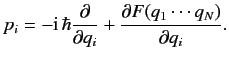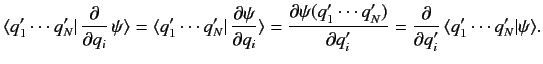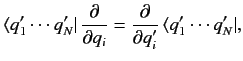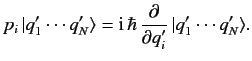Next: Momentum Representation
Up: Position and Momentum
Previous: Schrödinger Representation
Generalized Schrödinger Representation
In the preceding section, we developed the Schrödinger representation
for the case of a single
operator  corresponding to a classical Cartesian coordinate. However, this scheme
can easily be extended. Consider a system with
corresponding to a classical Cartesian coordinate. However, this scheme
can easily be extended. Consider a system with 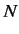 generalized coordinates,
generalized coordinates,
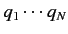 , which can all be simultaneously measured. These are represented
as
, which can all be simultaneously measured. These are represented
as 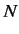 commuting operators,
commuting operators,
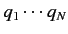 , each with a continuous range
of eigenvalues,
, each with a continuous range
of eigenvalues,
 .
Ket space is conveniently spanned by the simultaneous
eigenkets of
.
Ket space is conveniently spanned by the simultaneous
eigenkets of
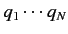 , which are denoted
, which are denoted
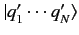 . These
eigenkets must form a complete set, otherwise the
. These
eigenkets must form a complete set, otherwise the
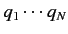 would not be
simultaneously observable.
would not be
simultaneously observable.
The orthogonality condition for the eigenkets [i.e., the generalization of
Equation (117)] is
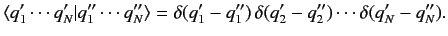 |
(150) |
The completeness condition [i.e., the generalization of Equation (118)] is
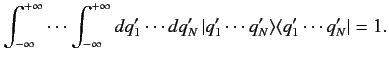 |
(151) |
The standard ket 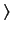 is defined such that
is defined such that
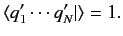 |
(152) |
The standard bra 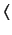 is the dual of the standard ket. A general state
ket is written
is the dual of the standard ket. A general state
ket is written
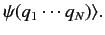 |
(153) |
The associated wavefunction is
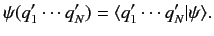 |
(154) |
Likewise, a general state bra is written
 |
(155) |
where
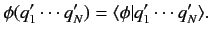 |
(156) |
The probability of an observation of the system simultaneously finding the first coordinate in
the range 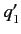 to
to
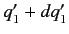 , the second coordinate in the range
, the second coordinate in the range 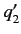 to
to
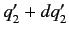 , etc., is
, etc., is
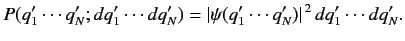 |
(157) |
Finally, the normalization condition for a physical wavefunction is
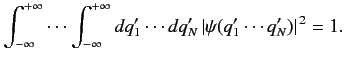 |
(158) |
The 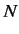 linear operators
linear operators
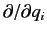 (where
(where 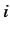 runs from 1 to
runs from 1 to 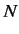 )
are defined
)
are defined
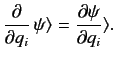 |
(159) |
These linear operators can also act on bras (provided the associated wavefunctions
are square integrable) in accordance with [see Equation (133)]
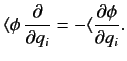 |
(160) |
Corresponding to Equation (137), we can derive the commutation relations
 |
(161) |
It is also clear that
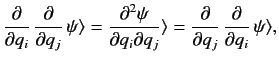 |
(162) |
showing that
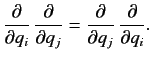 |
(163) |
It can be seen, by comparison with Equations (114)-(116), that the linear operators
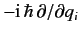 satisfy the same commutation relations
with the
satisfy the same commutation relations
with the 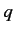 's
and with each other that the
's
and with each other that the 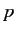 's do. The most general conclusion
we can draw from this coincidence of commutation relations is (see Dirac)
's do. The most general conclusion
we can draw from this coincidence of commutation relations is (see Dirac)
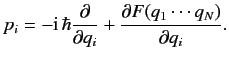 |
(164) |
However, the function 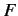 can be transformed away via a suitable readjustment of the phases
of the basis eigenkets (see Section 2.4, and Dirac). Thus, we can always construct
a set of simultaneous eigenkets of
can be transformed away via a suitable readjustment of the phases
of the basis eigenkets (see Section 2.4, and Dirac). Thus, we can always construct
a set of simultaneous eigenkets of
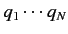 for which
for which
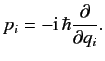 |
(165) |
This is the generalized Schrödinger representation.
It follows from Equations (152), (159), and (165) that
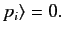 |
(166) |
Thus, the standard ket in the Schrödinger representation is a simultaneous eigenket
of all the momentum operators belonging to the eigenvalue zero. Note that
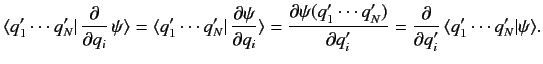 |
(167) |
Hence,
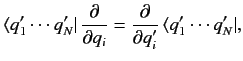 |
(168) |
so that
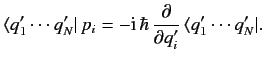 |
(169) |
The dual of the above equation gives
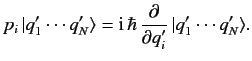 |
(170) |



Next: Momentum Representation
Up: Position and Momentum
Previous: Schrödinger Representation
Richard Fitzpatrick
2013-04-08
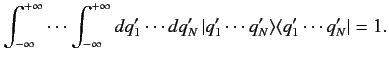
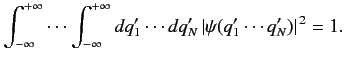
![]() linear operators
linear operators
![]() (where
(where ![]() runs from 1 to
runs from 1 to ![]() )
are defined
)
are defined
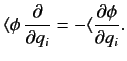

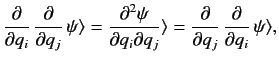
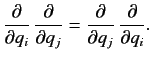
![]() satisfy the same commutation relations
with the
satisfy the same commutation relations
with the ![]() 's
and with each other that the
's
and with each other that the ![]() 's do. The most general conclusion
we can draw from this coincidence of commutation relations is (see Dirac)
's do. The most general conclusion
we can draw from this coincidence of commutation relations is (see Dirac)