Next: Schrödinger Representation
Up: Position and Momentum
Previous: Poisson Brackets
Consider a simple system with one classical degree of freedom, which corresponds to
the Cartesian coordinate 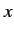 . Suppose that
. Suppose that 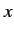 is free to take any value (e.g.,
is free to take any value (e.g.,
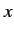 could be the position of a free particle). The classical dynamical variable
could be the position of a free particle). The classical dynamical variable
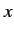 is represented in quantum
mechanics as a linear Hermitian operator which is also called
is represented in quantum
mechanics as a linear Hermitian operator which is also called 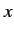 .
Moreover, the operator
.
Moreover, the operator 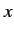 possesses eigenvalues
possesses eigenvalues  lying in the continuous
range
lying in the continuous
range
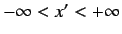 (since the eigenvalues
correspond to all the possible results of a measurement of
(since the eigenvalues
correspond to all the possible results of a measurement of 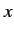 ). We can
span ket space using the suitably normalized eigenkets of
). We can
span ket space using the suitably normalized eigenkets of 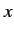 .
An eigenket corresponding to the eigenvalue
.
An eigenket corresponding to the eigenvalue  is denoted
is denoted
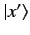 .
Moreover,
[see Equation (85)]
.
Moreover,
[see Equation (85)]
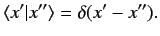 |
(117) |
The eigenkets satisfy the extremely useful relation [see Equation (87)]
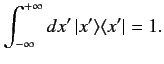 |
(118) |
This formula expresses the fact that the eigenkets are complete, mutually
orthogonal, and suitably normalized.
A state ket 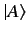 (which represents a general state
(which represents a general state 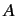 of the system)
can be expressed as a linear superposition of the eigenkets of the position
operator using Equation (118). Thus,
of the system)
can be expressed as a linear superposition of the eigenkets of the position
operator using Equation (118). Thus,
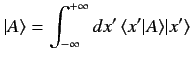 |
(119) |
The quantity
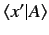 is a complex function of the position eigenvalue
is a complex function of the position eigenvalue
 . We can write
. We can write
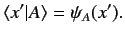 |
(120) |
Here,
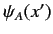 is the famous wavefunction of quantum mechanics.
Note that state
is the famous wavefunction of quantum mechanics.
Note that state 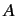 is completely specified by its wavefunction
is completely specified by its wavefunction
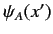 [because the wavefunction can be used to reconstruct the state ket
[because the wavefunction can be used to reconstruct the state ket 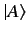 using Equation (119)].
It is clear that the wavefunction of state
using Equation (119)].
It is clear that the wavefunction of state 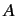 is simply the collection
of the weights of the corresponding state ket
is simply the collection
of the weights of the corresponding state ket 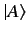 ,
when it is expanded in terms of the eigenkets of the
position operator. Recall, from Section 1.10, that the probability of
a measurement of a dynamical variable
,
when it is expanded in terms of the eigenkets of the
position operator. Recall, from Section 1.10, that the probability of
a measurement of a dynamical variable  yielding the result
yielding the result 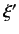 when the system is in state
when the system is in state 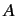 is given by
is given by
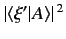 , assuming that
the
eigenvalues of
, assuming that
the
eigenvalues of  are discrete. This result is easily generalized to dynamical
variables possessing continuous eigenvalues. In fact, the probability of
a measurement of
are discrete. This result is easily generalized to dynamical
variables possessing continuous eigenvalues. In fact, the probability of
a measurement of 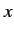 yielding a result lying in the range
yielding a result lying in the range  to
to 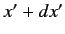 when the system is in a state
when the system is in a state 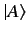 is
is
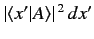 .
In other words, the probability of a measurement of position yielding a
result in the range
.
In other words, the probability of a measurement of position yielding a
result in the range  to
to 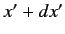 when the wavefunction of the system is
when the wavefunction of the system is
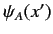 is
is
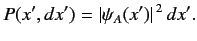 |
(121) |
This formula is only valid if the state ket 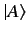 is properly normalized:
i.e., if
is properly normalized:
i.e., if
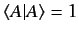 . The corresponding normalization for
the wavefunction is
. The corresponding normalization for
the wavefunction is
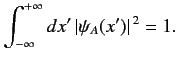 |
(122) |
Consider a second state 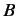 represented by a state ket
represented by a state ket 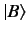 and
a wavefunction
and
a wavefunction
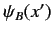 . The inner product
. The inner product
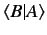 can be written
can be written
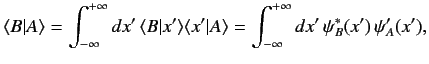 |
(123) |
where use has been made of Equations (118) and (120). Thus, the inner product of two states is
related to the overlap integral of their wavefunctions.
Consider a general function 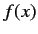 of the observable
of the observable 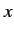 [e.g.,
[e.g., 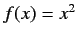 ].
If
].
If
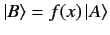 then it follows that
then it follows that
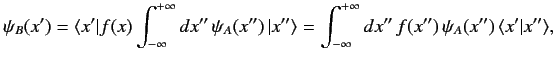 |
(124) |
giving
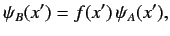 |
(125) |
where use has been made of Equation (117). Here, 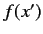 is the same function
of the position eigenvalue
is the same function
of the position eigenvalue  that
that 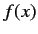 is of the position operator
is of the position operator 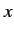 :
i.e., if
:
i.e., if 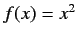 then
then
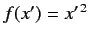 . It follows, from the above result,
that a general state ket
. It follows, from the above result,
that a general state ket
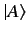 can be written
can be written
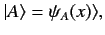 |
(126) |
where 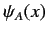 is the same function of the operator
is the same function of the operator 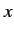 that the wavefunction
that the wavefunction
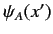 is of the position eigenvalue
is of the position eigenvalue  , and the ket
, and the ket 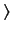 has the
wavefunction
has the
wavefunction
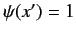 . The ket
. The ket 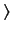 is termed the standard ket.
The dual of the standard ket is termed the standard bra, and is
denoted
is termed the standard ket.
The dual of the standard ket is termed the standard bra, and is
denoted 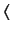 . It is
easily seen that
. It is
easily seen that
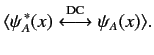 |
(127) |
Note, finally, that
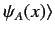 is often shortened to
is often shortened to
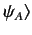 , leaving
the dependence on the position operator
, leaving
the dependence on the position operator 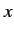 tacitly understood.
tacitly understood.



Next: Schrödinger Representation
Up: Position and Momentum
Previous: Poisson Brackets
Richard Fitzpatrick
2013-04-08
![]() (which represents a general state
(which represents a general state ![]() of the system)
can be expressed as a linear superposition of the eigenkets of the position
operator using Equation (118). Thus,
of the system)
can be expressed as a linear superposition of the eigenkets of the position
operator using Equation (118). Thus,
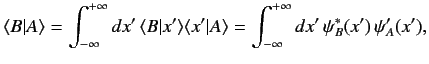
![]() of the observable
of the observable ![]() [e.g.,
[e.g., ![]() ].
If
].
If
![]() then it follows that
then it follows that