


Next: Identical Particles
Up: Time-Dependent Perturbation Theory
Previous: Photo-Ionization
- Consider the two-state system examined in Section 8.3. Suppose that
where 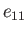 ,
, 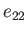 ,
, 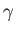 , and
, and 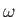 are real. Show that
are real. Show that
where
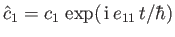 ,
,
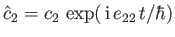 , and
, and
Hence, deduce that if the system is definitely in state 1 at time  then the probability of finding it in state 2
at some subsequent time,
then the probability of finding it in state 2
at some subsequent time, 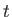 , is
, is
- Consider an atomic nucleus of spin-
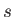 and
and  -factor
-factor  placed in the magnetic field
placed in the magnetic field
where
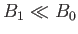 . Let
. Let
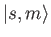 be a properly normalized simultaneous eigenket of
be a properly normalized simultaneous eigenket of  and
and
 , where
, where 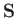 is the nuclear spin. Thus,
is the nuclear spin. Thus,
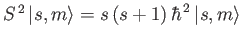 and
and
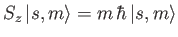 , where
, where
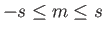 . Furthermore, the instantaneous nuclear
spin state is written
. Furthermore, the instantaneous nuclear
spin state is written
where
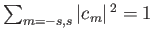 .
.
- Demonstrate that
for
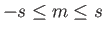 , where
, where
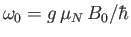 and
and
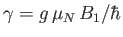 .
.
- Consider the case
 . Demonstrate that if
. Demonstrate that if
 and
and
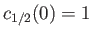 then
then
- Consider the case
 . Demonstrate that if
. Demonstrate that if
 and
and
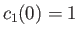 then
then
- Consider the case
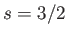 . Demonstrate that if
. Demonstrate that if
 and
and
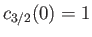 then
then
- Derive Equation (8.45).
- Derive Equation (8.83).
- If
is the probability that a system initially in state 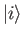 at time
at time  is still in that
state at some subsequent time, deduce that the mean lifetime of the state is
is still in that
state at some subsequent time, deduce that the mean lifetime of the state is 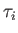 .
.
- Demonstrate that
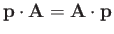 when
when
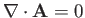 , where
, where
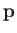 is the momentum operator, and
is the momentum operator, and
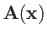 is a real function of the position operator,
is a real function of the position operator, 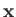 .
Hence, show that the Hamiltonian (8.128) is Hermitian.
.
Hence, show that the Hamiltonian (8.128) is Hermitian.
- Demonstrate that
where the average is taken over all possible directions of the unit vector
 .
.
- Demonstrate that
where
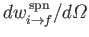 is specified by Equation (8.165).
[Hint: Write
is specified by Equation (8.165).
[Hint: Write
where
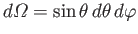 .]
.]
- Demonstrate that a spontaneous transition between two atomic states of zero orbital
angular momentum is absolutely forbidden. (Actually, a spontaneous transition between
two zero orbital angular momentum states is possible via the simultaneous emission of two photons, but takes place at a very slow rate [56,15,102].)
- Find the selection rules for the matrix elements
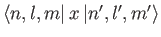 and
and
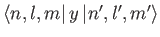 to
be non-zero. Here,
to
be non-zero. Here,
 denotes an energy eigenket of a hydrogen-like
atom corresponding to the conventional quantum numbers,
denotes an energy eigenket of a hydrogen-like
atom corresponding to the conventional quantum numbers,  ,
,  , and
, and  .
.
- The Hamiltonian of an electron in a hydrogen-like atom is written
where
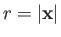 . Let
. Let 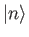 denote a properly normalized energy eigenket belonging to the eigenvalue
denote a properly normalized energy eigenket belonging to the eigenvalue  . By calculating
. By calculating
![$ [[H, x_i], \,x_i]$](img2861.png) , derive the Thomas-Reiche-Kuhn sum rule,
, derive the Thomas-Reiche-Kuhn sum rule,
where
and
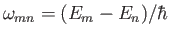 , and the sum is over all energy eigenstates. Here,
, and the sum is over all energy eigenstates. Here, 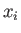 stands for either
stands for either  ,
,  , or
, or  . (See Exercise 6.)
. (See Exercise 6.)
-
- Show that the only non-zero
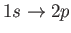 electric dipole matrix elements for the
hydrogen atom
take the values
electric dipole matrix elements for the
hydrogen atom
take the values
where 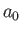 is the Bohr radius.
is the Bohr radius.
- Likewise, show that the only non-zero
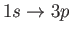 electric dipole matrix elements
take the values
electric dipole matrix elements
take the values
- Finally, show that the only non-zero
 electric dipole matrix elements
take the values
electric dipole matrix elements
take the values
-
- Demonstrate that the spontaneous decay rate (via an electric dipole transition) from any
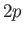 state to a
state to a  state
of a hydrogen atom is
state
of a hydrogen atom is
where 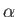 is the fine structure constant.
Hence, deduce that the relative natural width of the associated spectral line is
is the fine structure constant.
Hence, deduce that the relative natural width of the associated spectral line is
where 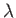 denotes wavelength.
denotes wavelength.
- Likewise, show that the spontaneous decay rate from any
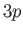 state to a
state to a  state
is
state
is
Hence, deduce that the relative natural width of the associated spectral line is
- Demonstrate that the net oscillator strength for
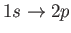 transitions in a hydrogen atom is
transitions in a hydrogen atom is
irrespective of the polarization of the radiation.
- Likewise, show that the net oscillator strength for
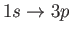 transitions is
transitions is
irrespective of the polarization of the radiation.
- Taking electron spin into account, the wavefunctions of the
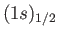 states of a hydrogen
atom are written
states of a hydrogen
atom are written
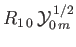 where
where 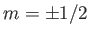 . Here, the
. Here, the 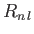 are
standard radial wavefunctions, and the
are
standard radial wavefunctions, and the
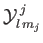 are spin-angular functions. Likewise, the
wavefunctions of the
are spin-angular functions. Likewise, the
wavefunctions of the
 states are written
states are written
 , where
, where
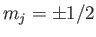 .
Finally, the wavefunctions of the
.
Finally, the wavefunctions of the
 states are written
states are written
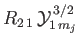 , where
, where 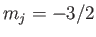 ,
,
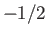 ,
, 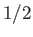 ,
, 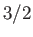 . As a consequence of spin-orbit interaction, the four
. As a consequence of spin-orbit interaction, the four
 states lie
at a slightly higher energy than the two
states lie
at a slightly higher energy than the two
 states. Demonstrate that the spontaneous decay
rates, due to electric dipole transitions, between the various
states. Demonstrate that the spontaneous decay
rates, due to electric dipole transitions, between the various 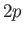 and
and  states are
states are
where
Here, the states have been labeled by their spin-angular functions.
Hence, deduce that for an ensemble of hydrogen atoms in thermal equilibrium, the spectral line associated with
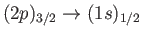 transitions is twice as bright as that associated with
transitions is twice as bright as that associated with
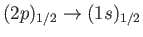 transitions.
transitions.
- Taking electron spin into account, the wavefunctions of the
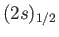 states of a hydrogen
atom are written
states of a hydrogen
atom are written
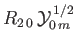 where
where 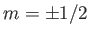 . The wavefunctions of the
. The wavefunctions of the
 states are specified in the previous exercise.
Demonstrate that the spontaneous decay
rates, due to electric dipole transitions, between the various
states are specified in the previous exercise.
Demonstrate that the spontaneous decay
rates, due to electric dipole transitions, between the various
 and
and
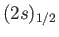 states are
states are
where
Here, the states have been labeled by their spin-angular functions.
- Consider the
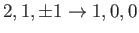 electric dipole transition of a hydrogen atom. Show that the angular distribution of spontaneously emitted photons is
electric dipole transition of a hydrogen atom. Show that the angular distribution of spontaneously emitted photons is
where
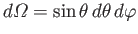 , and the photon's direction of motion is parallel to
, and the photon's direction of motion is parallel to
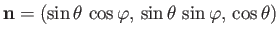 .
.
- Consider the
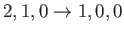 electric dipole transition of a hydrogen atom. Show that the angular distribution of spontaneously emitted photons is
electric dipole transition of a hydrogen atom. Show that the angular distribution of spontaneously emitted photons is
- Hence, show that for an ensemble of hydrogen atoms in thermal equilibrium, the angular distribution of
spontaneously emitted photons associated with the
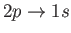 electric dipole transition is
electric dipole transition is
- The properly normalized
 triplet and singlet state kets of a hydrogen atom can be written
triplet and singlet state kets of a hydrogen atom can be written
and
respectively. Here, the kets on the left are
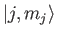 kets, where
kets, where 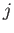 and
and 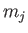 are the conventional
quantum numbers that determine the overall angular momentum, and the projection of the overall
angular momentum along the
are the conventional
quantum numbers that determine the overall angular momentum, and the projection of the overall
angular momentum along the  -axis, respectively. Finally,
-axis, respectively. Finally,
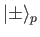 and
and
 are the
properly normalized spin-up and spin-down states for the proton and the electron, respectively.
As explained in Section 7.9, the triplet states have slightly higher energies than the
singlet state, as a consequence of spin-spin coupling between the proton and the electron. Spontaneous
magnetic dipole transitions between the triplet and singlet states occur via the interaction of the
magnetic component of the emitted photon and the electron magnetic moment. (The magnetic moment
of the proton is much smaller than that of the electron, and consequently does not play a significant role
in this transition.) In the following, the initial state,
are the
properly normalized spin-up and spin-down states for the proton and the electron, respectively.
As explained in Section 7.9, the triplet states have slightly higher energies than the
singlet state, as a consequence of spin-spin coupling between the proton and the electron. Spontaneous
magnetic dipole transitions between the triplet and singlet states occur via the interaction of the
magnetic component of the emitted photon and the electron magnetic moment. (The magnetic moment
of the proton is much smaller than that of the electron, and consequently does not play a significant role
in this transition.) In the following, the initial state, 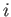 , corresponds to one of the triplet states, and the final
state,
, corresponds to one of the triplet states, and the final
state,  , corresponds to the singlet state.
, corresponds to the singlet state.
- Demonstrate that
where 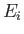 and
and  are the energies of the initial and final states, and
are the energies of the initial and final states, and 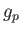 is the proton
is the proton  -factor.
-factor.
- Let
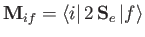 be the magnetic dipole matrix element, where
be the magnetic dipole matrix element, where
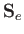 is the electron spin.
Show that
is the electron spin.
Show that
if the initial state is the
 state,
state,
if the initial state is the
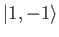 state,
and
state,
and
if the initial state is the
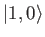 state.
state.
- Deduce that the angular distribution of the spontaneously emitted photon is
if the initial state is either the
 state or the
state or the
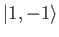 state.
Show that the angular distribution is
state.
Show that the angular distribution is
if the initial state is the
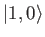 state. Here, the photon's direction of motion is
parallel to
state. Here, the photon's direction of motion is
parallel to
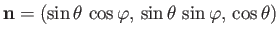 .
.
- Finally, show that the overall spontaneous transition rate is
- Consider the
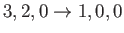 electric quadrupole transition of a hydrogen atom.
electric quadrupole transition of a hydrogen atom.
- Show that the angular distribution of spontaneously emitted photons can be written
- Demonstrate that the only non-zero
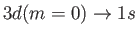 electric quadrupole matrix elements takes the values
electric quadrupole matrix elements takes the values
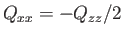 ,
,
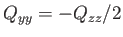 , and
, and
- Hence, deduce that
and
Here, the spontaneously emitted photon's direction of motion is
parallel to
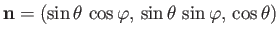 .
.
- Let
where  is a non-negative integer.
Demonstrate that
is a non-negative integer.
Demonstrate that
and
Hence, deduce that
and
- Treating
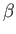 as a small parameter, and neglecting terms of order
as a small parameter, and neglecting terms of order
 , show that
, show that
- Repeat the calculation of Section 8.15 for the case where the electric polarization vector
of the incident photon is

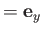 . Hence, show that, in this case, the differential
photo-ionization cross-section is
. Hence, show that, in this case, the differential
photo-ionization cross-section is
Deduce that the photo-ionization cross-section for unpolarized electromagnetic radiation propagating in the  -direction
is
-direction
is
- Consider the photo-ionization of a hydrogen atom in the
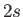 state. Demonstrate that formula (8.249)
is replaced by
state. Demonstrate that formula (8.249)
is replaced by
- Consider the inverse process to the photo-ionization of a hydrogen atom investigated in Section 8.15.
In this process, which is known as radiative association, an unbound electron of energy
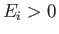 is captured by a (stationary) proton to form a hydrogen
atom in its ground state, with the emission of a photon of energy
is captured by a (stationary) proton to form a hydrogen
atom in its ground state, with the emission of a photon of energy
where
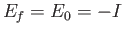 . Here,
. Here, 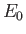 is (negative) hydrogen ground-state energy, and
is (negative) hydrogen ground-state energy, and 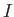 is
the (positive) ground-state ionization energy. Radiative association can be thought of as a form of
stimulated emission in which the initial state is unbound. Thus, according to the analysis of Section 8.9,
is
the (positive) ground-state ionization energy. Radiative association can be thought of as a form of
stimulated emission in which the initial state is unbound. Thus, according to the analysis of Section 8.9,
where 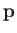 is the electron momentum,
is the electron momentum, 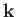 is the wavevector of the emitted photon, and
is the wavevector of the emitted photon, and
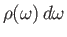 is the number of photon states whose angular frequencies lie between
is the number of photon states whose angular frequencies lie between 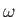 and
and
 , and whose
direction of motion lie in the range of solid angles
, and whose
direction of motion lie in the range of solid angles
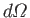 . Here,
. Here,

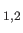 are two independent
unit vectors normal to
are two independent
unit vectors normal to 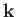 .
.
- Show that
where the initial electron and final photon are both assumed to be contained in a periodic
box of volume
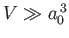 .
.
- Hence, demonstrate that
where
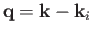 , and
, and
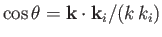 .
.
- Finally, show that
where
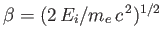 .
.



Next: Identical Particles
Up: Time-Dependent Perturbation Theory
Previous: Photo-Ionization
Richard Fitzpatrick
2016-01-22

![$\displaystyle = \frac{\gamma}{2}\,\exp\left[+{\rm i}\,(\omega-\hat{\omega}_{21})\,t\right]\hat{c}_2,$](img2809.png)
![$\displaystyle = \frac{\gamma}{2}\,\exp\left[-{\rm i}\,(\omega-\hat{\omega}_{21})\,t\right]\hat{c}_1,$](img2811.png)
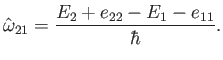
![$\displaystyle P_2(t) = \frac{\gamma^{\,2}}{ \gamma^{\,2} +
(\omega-\hat{\omega...
...gamma^{\,2}+
(\omega-\hat{\omega}_{21})^{\,2}\right]^{1/2} \frac{t}{2}\right).
$](img2815.png)
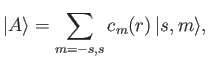

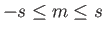 , where
, where
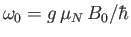 and
and
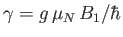 .
.
 . Demonstrate that if
. Demonstrate that if
 and
and
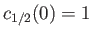 then
then
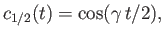
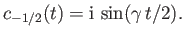
 . Demonstrate that if
. Demonstrate that if
 and
and
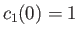 then
then


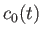


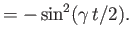
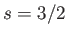 . Demonstrate that if
. Demonstrate that if
 and
and
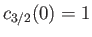 then
then
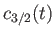
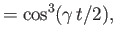

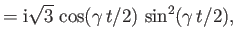
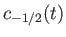
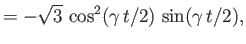
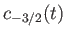

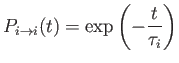
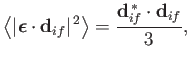
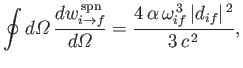
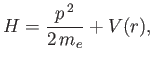
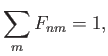
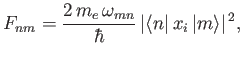
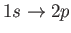 electric dipole matrix elements for the
hydrogen atom
take the values
electric dipole matrix elements for the
hydrogen atom
take the values

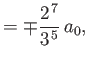
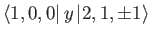
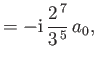
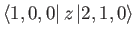
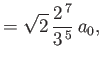
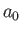 is the Bohr radius.
is the Bohr radius.
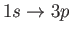 electric dipole matrix elements
take the values
electric dipole matrix elements
take the values

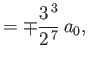

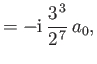
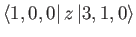
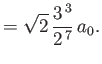
 electric dipole matrix elements
take the values
electric dipole matrix elements
take the values
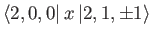
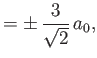
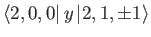
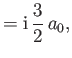
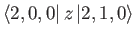
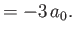
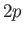 state to a
state to a  state
of a hydrogen atom is
state
of a hydrogen atom is
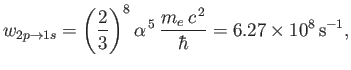
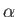 is the fine structure constant.
Hence, deduce that the relative natural width of the associated spectral line is
is the fine structure constant.
Hence, deduce that the relative natural width of the associated spectral line is
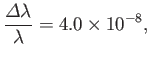
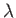 denotes wavelength.
denotes wavelength.
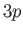 state to a
state to a  state
is
state
is
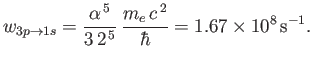
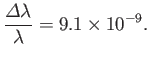
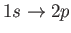 transitions in a hydrogen atom is
transitions in a hydrogen atom is
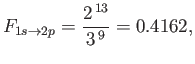
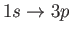 transitions is
transitions is
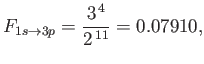
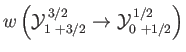

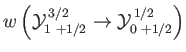
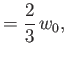
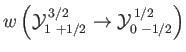
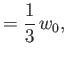
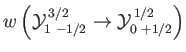
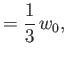
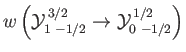
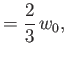
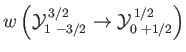
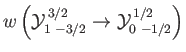
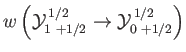
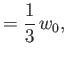

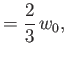

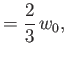
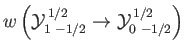
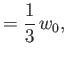

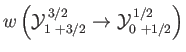

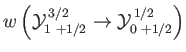
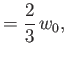
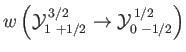
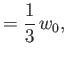
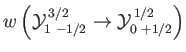
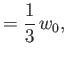
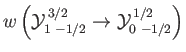
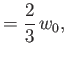
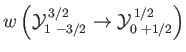
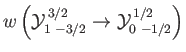
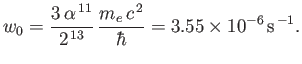
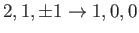 electric dipole transition of a hydrogen atom. Show that the angular distribution of spontaneously emitted photons is
electric dipole transition of a hydrogen atom. Show that the angular distribution of spontaneously emitted photons is
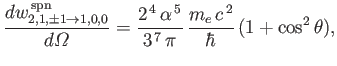
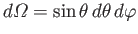 , and the photon's direction of motion is parallel to
, and the photon's direction of motion is parallel to
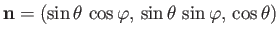 .
.
 electric dipole transition of a hydrogen atom. Show that the angular distribution of spontaneously emitted photons is
electric dipole transition of a hydrogen atom. Show that the angular distribution of spontaneously emitted photons is

 electric dipole transition is
electric dipole transition is
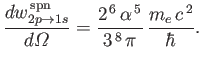
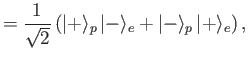
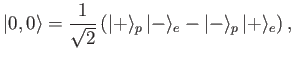
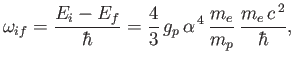
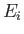 and
and  are the energies of the initial and final states, and
are the energies of the initial and final states, and 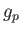 is the proton
is the proton  -factor.
-factor.
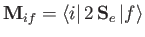 be the magnetic dipole matrix element, where
be the magnetic dipole matrix element, where
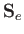 is the electron spin.
Show that
is the electron spin.
Show that

 state,
state,

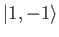 state,
and
state,
and
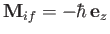
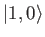 state.
state.

 state or the
state or the
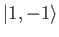 state.
Show that the angular distribution is
state.
Show that the angular distribution is

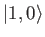 state. Here, the photon's direction of motion is
parallel to
state. Here, the photon's direction of motion is
parallel to
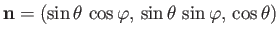 .
.
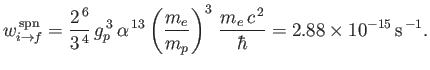
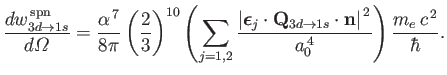
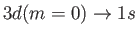 electric quadrupole matrix elements takes the values
electric quadrupole matrix elements takes the values
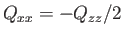 ,
,
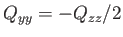 , and
, and

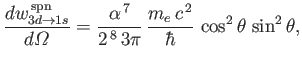

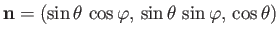 .
.
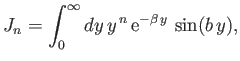
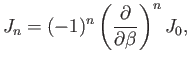



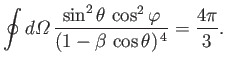
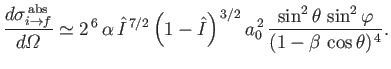
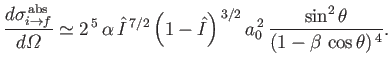
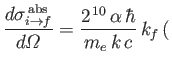
![$\displaystyle \cdot{\bf k}_f)^{\,2}\,a_0^{\,3} \,\frac{\left[1-(2\,q\,a_0)^2\right]^{\,2}}{\left[1+(2\,q\,a_0)^2\right]^{\,6}}.
$](img2967.png)
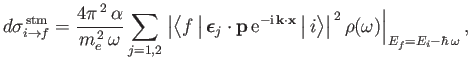
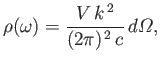
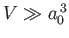 .
.
![$\displaystyle \frac{d\sigma_{i\rightarrow f}^{\,\rm stm}}{d{\mit\Omega}} = \fra...
...\,2}}\,\frac{k\,k_i^{\,2}\,a_0^{\,2}\,\sin^2\theta}{[1+(q\,a_0)^{\,2}]^{\,4}},
$](img2977.png)
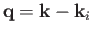 , and
, and
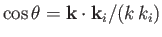 .
.
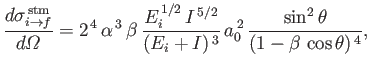
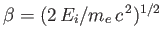 .
.