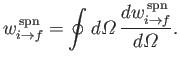Next: Electric Dipole Transitions
Up: Time-Dependent Perturbation Theory
Previous: Absorption and Stimulated Emission
Spontaneous Emission of Radiation
So far, we have calculated the transition rates
between two atomic states induced by external electromagnetic radiation. This process is known as absorption when the energy of the final state exceeds that
of the initial state, and stimulated emission when the energy of the final state is less than that
of the initial state. Now, in the absence of any external radiation, we would
not expect an atom in a given state to spontaneously jump into a
state with a higher energy. On the other hand, it should be possible for
such an atom to spontaneously jump into an state with a lower energy
via the emission of a photon whose energy is equal to the difference
between the energies of the initial and final states. This process is known as spontaneous emission.
We can derive the rate of spontaneous emission between two atomic states
from a knowledge of the corresponding absorption and stimulated
emission rates using a famous thermodynamic argument initially formulated by Einstein [38].
Consider a very large ensemble of similar atoms placed inside a closed cavity whose walls (which are assumed to be perfect emitters and absorbers of radiation) are held at
the constant temperature 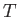 . Let the system have attained thermal equilibrium.
According to statistical thermodynamics, the cavity is filled with so-called black-body electromagnetic
radiation whose energy spectrum is [91]
. Let the system have attained thermal equilibrium.
According to statistical thermodynamics, the cavity is filled with so-called black-body electromagnetic
radiation whose energy spectrum is [91]
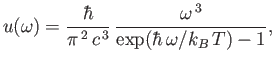 |
(8.153) |
where 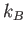 is the Boltzmann constant. This well-known result was first
obtained by Max Planck in 1900 [82,83].
is the Boltzmann constant. This well-known result was first
obtained by Max Planck in 1900 [82,83].
Consider two atomic states, labeled 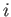 and
and  , with
, with 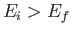 . One
of the tenants of statistical thermodynamics is that in thermal equilibrium
we have so-called detailed balance. (See Section 8.8.) This means that, irrespective
of any other atomic states, the rate at which atoms in the ensemble leave
state
. One
of the tenants of statistical thermodynamics is that in thermal equilibrium
we have so-called detailed balance. (See Section 8.8.) This means that, irrespective
of any other atomic states, the rate at which atoms in the ensemble leave
state 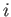 due to transitions to state
due to transitions to state  is exactly balanced by the
rate at which atoms enter state
is exactly balanced by the
rate at which atoms enter state 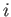 due to transitions from state
due to transitions from state  .
The former rate (i.e., number of transitions per unit time in the ensemble) is written
.
The former rate (i.e., number of transitions per unit time in the ensemble) is written
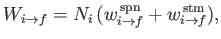 |
(8.154) |
where
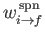 and
and
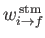 are the rates of spontaneous and stimulated emission,
respectively,
(for a single atom) between
states
are the rates of spontaneous and stimulated emission,
respectively,
(for a single atom) between
states 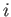 and
and  , and
, and 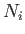 is the number of atoms in the ensemble
in state
is the number of atoms in the ensemble
in state 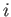 . Likewise, the latter rate takes the form
. Likewise, the latter rate takes the form
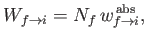 |
(8.155) |
where
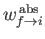 is the rate of absorption (for a single atom) between states
is the rate of absorption (for a single atom) between states  and
and 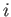 , and
, and 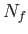 is the number of atoms in the ensemble in state
is the number of atoms in the ensemble in state  .
The previous expressions describe how atoms in the ensemble make transitions from
state
.
The previous expressions describe how atoms in the ensemble make transitions from
state 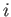 to state
to state  via a combination of spontaneous and stimulated emission, and make the reverse transition as a consequence of absorption.
In thermal equilibrium, we have
via a combination of spontaneous and stimulated emission, and make the reverse transition as a consequence of absorption.
In thermal equilibrium, we have
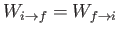 ,
which gives
,
which gives
 |
(8.156) |
Equations (8.149) and (8.150) imply that
 |
(8.157) |
where
 , and the large angle brackets denote an average over all possible polarization directions of the incident radiation (because, in equilibrium, the
radiation inside the cavity is isotropic).
In fact, it is easily demonstrated that
, and the large angle brackets denote an average over all possible polarization directions of the incident radiation (because, in equilibrium, the
radiation inside the cavity is isotropic).
In fact, it is easily demonstrated that
 |
(8.158) |
where
 |
(8.159) |
(See Exercise 7.)
Now, another famous result in statistical thermodynamics is that,
in thermal equilibrium, the number of atoms in an ensemble occupying
a state of energy  is proportional to
is proportional to
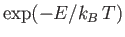 [91]. This implies
that
[91]. This implies
that
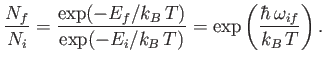 |
(8.160) |
Thus, it follows from Equations (8.156), (8.160), (8.161), and (8.163) that the rate of spontaneous emission between states
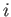 and
and  takes the form
takes the form
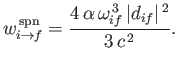 |
(8.161) |
Note, that, although the previous result has been derived for
an atom in a radiation-filled cavity, it remains correct even in the absence
of radiation.
The direction of propagation of a photon spontaneously emitted by an atom is specified by its normalized wavevector, 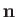 .
Likewise, the electric polarization direction of the photon is specified by the unit vector
.
Likewise, the electric polarization direction of the photon is specified by the unit vector
 .
However,
.
However,

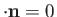 , which implies that
, which implies that

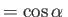

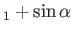

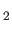 ,
where
,
where
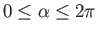 . Here, the unit vectors
. Here, the unit vectors

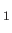 ,
,

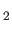 , and
, and 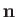 are
mutually perpendicular, and form a right-handed set (i.e.,
are
mutually perpendicular, and form a right-handed set (i.e.,


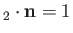 ).
The vectors
).
The vectors

 and
and

 represent the two possible independent electric polarization directions of
the emitted photon. Equation (8.164) generalizes to give [77]
represent the two possible independent electric polarization directions of
the emitted photon. Equation (8.164) generalizes to give [77]
where
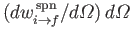 is the rate of spontaneous
emission of photons whose propagation directions lie in the range of solid angle
is the rate of spontaneous
emission of photons whose propagation directions lie in the range of solid angle
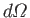 .
Of course,
.
Of course,
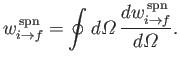 |
(8.163) |
(See Exercise 8.)



Next: Electric Dipole Transitions
Up: Time-Dependent Perturbation Theory
Previous: Absorption and Stimulated Emission
Richard Fitzpatrick
2016-01-22
![]() . Let the system have attained thermal equilibrium.
According to statistical thermodynamics, the cavity is filled with so-called black-body electromagnetic
radiation whose energy spectrum is [91]
. Let the system have attained thermal equilibrium.
According to statistical thermodynamics, the cavity is filled with so-called black-body electromagnetic
radiation whose energy spectrum is [91]
![]() and
and ![]() , with
, with ![]() . One
of the tenants of statistical thermodynamics is that in thermal equilibrium
we have so-called detailed balance. (See Section 8.8.) This means that, irrespective
of any other atomic states, the rate at which atoms in the ensemble leave
state
. One
of the tenants of statistical thermodynamics is that in thermal equilibrium
we have so-called detailed balance. (See Section 8.8.) This means that, irrespective
of any other atomic states, the rate at which atoms in the ensemble leave
state ![]() due to transitions to state
due to transitions to state ![]() is exactly balanced by the
rate at which atoms enter state
is exactly balanced by the
rate at which atoms enter state ![]() due to transitions from state
due to transitions from state ![]() .
The former rate (i.e., number of transitions per unit time in the ensemble) is written
.
The former rate (i.e., number of transitions per unit time in the ensemble) is written
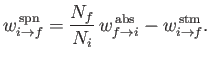
![]() .
Likewise, the electric polarization direction of the photon is specified by the unit vector
.
Likewise, the electric polarization direction of the photon is specified by the unit vector
![]() .
However,
.
However,
![]()
![]() , which implies that
, which implies that
![]()
![]()
![]()
![]()
![]()
![]() ,
where
,
where
![]() . Here, the unit vectors
. Here, the unit vectors
![]()
![]() ,
,
![]()
![]() , and
, and ![]() are
mutually perpendicular, and form a right-handed set (i.e.,
are
mutually perpendicular, and form a right-handed set (i.e.,
![]()
![]()
![]()
![]() ).
The vectors
).
The vectors
![]()
![]() and
and
![]()
![]() represent the two possible independent electric polarization directions of
the emitted photon. Equation (8.164) generalizes to give [77]
represent the two possible independent electric polarization directions of
the emitted photon. Equation (8.164) generalizes to give [77]