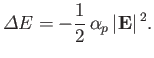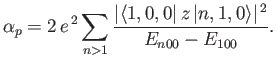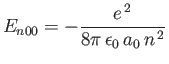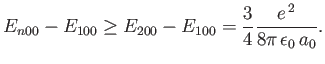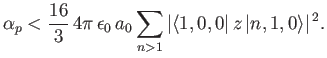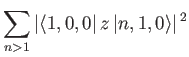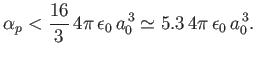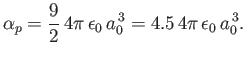Next: Degenerate Perturbation Theory
Up: Time-Independent Perturbation Theory
Previous: Non-Degenerate Perturbation Theory
Quadratic Stark Effect
The Stark effect is a phenomenon by which the energy eigenstates of an atomic or
molecular system are modified in the presence of a static, external, electric field. This phenomenon
was first observed experimentally (in hydrogen) by J. Stark in 1913 [105].
Let us employ perturbation theory to investigate the Stark effect.
Suppose that a hydrogen-like atom [i.e., either a hydrogen atom, or an alkali metal
atom (which possesses one valance electron orbiting outside a closed, spherically
symmetric, shell)] is subjected to a uniform electric field,  , pointing in the positive
, pointing in the positive
 -direction. The Hamiltonian of the system can be split into two
parts. The unperturbed Hamiltonian,
-direction. The Hamiltonian of the system can be split into two
parts. The unperturbed Hamiltonian,
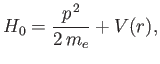 |
(7.38) |
and the perturbing Hamiltonian,
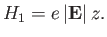 |
(7.39) |
It is assumed that the unperturbed energy eigenvalues and eigenstates are completely
known. The electron spin is irrelevant in this problem (because the spin operators
all commute with 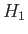 ), so we can ignore the spin degrees of freedom of the system.
This implies that the system possesses no degenerate energy eigenvalues. Actually, this is
not true for the
), so we can ignore the spin degrees of freedom of the system.
This implies that the system possesses no degenerate energy eigenvalues. Actually, this is
not true for the 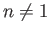 energy levels of the hydrogen atom, because of the special
properties of a pure Coulomb potential. (See Section 4.6.)
It is necessary to deal with this case separately, because
the perturbation theory presented in Section 7.3 breaks down for degenerate
unperturbed energy levels. (See Section 7.5.)
energy levels of the hydrogen atom, because of the special
properties of a pure Coulomb potential. (See Section 4.6.)
It is necessary to deal with this case separately, because
the perturbation theory presented in Section 7.3 breaks down for degenerate
unperturbed energy levels. (See Section 7.5.)
An energy eigenket of the unperturbed Hamiltonian is characterized by three quantum numbers--the principal quantum number  , and the azimuthal and magnetic quantum numbers,
, and the azimuthal and magnetic quantum numbers,  and
and
 , respectively. (See Section 4.6.) Let us denote such a ket
, respectively. (See Section 4.6.) Let us denote such a ket
 , and let its
energy be
, and let its
energy be 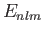 . According to Equation (7.32), the change in this
energy induced by a small external electric field (i.e., small compared to the typical electric field internal to the atom) is given by
. According to Equation (7.32), the change in this
energy induced by a small external electric field (i.e., small compared to the typical electric field internal to the atom) is given by
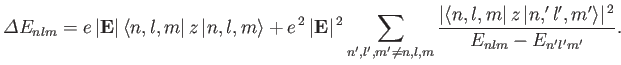 |
(7.40) |
Now, because
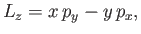 |
(7.41) |
it follows that
![$\displaystyle [L_z, z] = 0.$](img1811.png) |
(7.42) |
(See Chapter 4.)
Thus,
![$\displaystyle \langle n,l, m\vert\, [L_z, z]\, \vert n',l',m'\rangle = 0,$](img1812.png) |
(7.43) |
giving
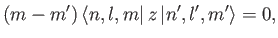 |
(7.44) |
because
 is, by definition, an eigenstate of
is, by definition, an eigenstate of  corresponding to the eigenvalue
corresponding to the eigenvalue
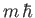 . It is clear, from the previous equation, that
the matrix element
. It is clear, from the previous equation, that
the matrix element
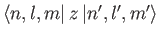 is zero unless
is zero unless  .
This is termed the selection rule for the magnetic quantum number,
.
This is termed the selection rule for the magnetic quantum number,  .
.
Let us now determine the selection rule for the azimuthal quantum number,  . We have
. We have
where use has been made of Equations (4.1)-(4.6).
Similarly,
Thus,
This reduces to
However, it is clear from Equations (4.1)-(4.3) that
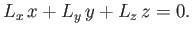 |
(7.50) |
Hence, we obtain
![$\displaystyle [L^2, [L^2, z]] = 2 \,\hbar^2\, (L^2\, z + z \,L^2),$](img1832.png) |
(7.51) |
which can be expanded to give
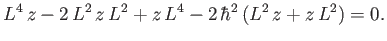 |
(7.52) |
Equation (7.52) implies that
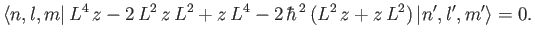 |
(7.53) |
Because
 is, by definition, an eigenstate of
is, by definition, an eigenstate of 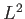 corresponding to the eigenvalue
corresponding to the eigenvalue
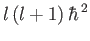 , the
previous expression yields
, the
previous expression yields
which reduces to
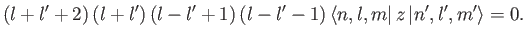 |
(7.54) |
According to the previous formula, the matrix element
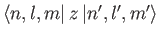 vanishes unless
vanishes unless 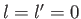 or
or
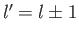 . This matrix element can be written
. This matrix element can be written
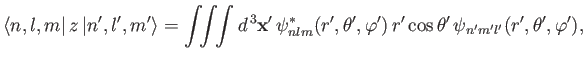 |
(7.55) |
where
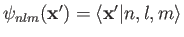 . Recall, however,
that the wavefunction of an
. Recall, however,
that the wavefunction of an  state is spherically symmetric: that is,
state is spherically symmetric: that is,
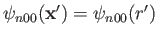 . (See Section 4.3.) It follows from Equation (7.56)
that the matrix element
vanishes, by symmetry, when
. (See Section 4.3.) It follows from Equation (7.56)
that the matrix element
vanishes, by symmetry, when 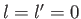 . In conclusion, the matrix element
. In conclusion, the matrix element
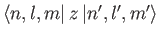 is zero unless
is zero unless 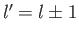 . This is
the selection rule for the quantum number
. This is
the selection rule for the quantum number  .
.
Application of the previously derived selection rules for  and
and  to Equation (7.40) yields
to Equation (7.40) yields
 |
(7.56) |
Note that all of the terms appearing in Equation (7.40) that vary linearly with
the electric field-strength
vanish, by symmetry, according to the selection rules.
Only those terms that vary quadratically with the
field-strength survive. Hence, the energy-shift specified in the previous formula is known as the
quadratic Stark effect.
The electrical polarizability, 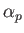 , of an atom is defined in terms
of the electric-field-induced energy-shift of a given atomic state as follows [67]:
, of an atom is defined in terms
of the electric-field-induced energy-shift of a given atomic state as follows [67]:
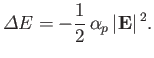 |
(7.57) |
Consider the ground state of a hydrogen atom. (Recall, that we cannot address
the 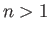 excited states because they are degenerate, and our theory cannot
deal with this at present). The polarizability of the ground state is given by
excited states because they are degenerate, and our theory cannot
deal with this at present). The polarizability of the ground state is given by
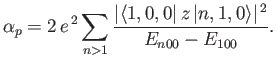 |
(7.58) |
Here, we have made use of the fact that
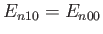 for a hydrogen atom. (See Section 4.6.)
for a hydrogen atom. (See Section 4.6.)
The sum in the previous expression can be evaluated approximately by noting that
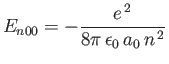 |
(7.59) |
for a hydrogen atom,
where
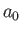 is the Bohr radius. [See Equation (4.132).] We can write
is the Bohr radius. [See Equation (4.132).] We can write
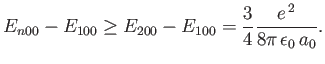 |
(7.60) |
Thus,
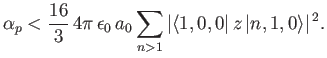 |
(7.61) |
However,
where we have made use of the fact that the wavefunctions of a hydrogen atom
form a complete set. It is easily demonstrated from the
actual form of the ground-state wavefunction
that
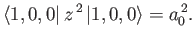 |
(7.63) |
(See Exercise 13.)
Thus, we conclude that
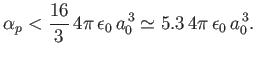 |
(7.64) |
The exact result is
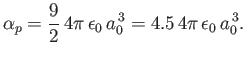 |
(7.65) |
It is possible to obtain this result, without recourse to perturbation
theory, by solving Schrödinger's equation in parabolic coordinates [115,41].



Next: Degenerate Perturbation Theory
Up: Time-Independent Perturbation Theory
Previous: Non-Degenerate Perturbation Theory
Richard Fitzpatrick
2016-01-22
![]() , pointing in the positive
, pointing in the positive
![]() -direction. The Hamiltonian of the system can be split into two
parts. The unperturbed Hamiltonian,
-direction. The Hamiltonian of the system can be split into two
parts. The unperturbed Hamiltonian,
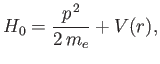
![]() ), so we can ignore the spin degrees of freedom of the system.
This implies that the system possesses no degenerate energy eigenvalues. Actually, this is
not true for the
), so we can ignore the spin degrees of freedom of the system.
This implies that the system possesses no degenerate energy eigenvalues. Actually, this is
not true for the ![]() energy levels of the hydrogen atom, because of the special
properties of a pure Coulomb potential. (See Section 4.6.)
It is necessary to deal with this case separately, because
the perturbation theory presented in Section 7.3 breaks down for degenerate
unperturbed energy levels. (See Section 7.5.)
energy levels of the hydrogen atom, because of the special
properties of a pure Coulomb potential. (See Section 4.6.)
It is necessary to deal with this case separately, because
the perturbation theory presented in Section 7.3 breaks down for degenerate
unperturbed energy levels. (See Section 7.5.)
![]() , and the azimuthal and magnetic quantum numbers,
, and the azimuthal and magnetic quantum numbers, ![]() and
and
![]() , respectively. (See Section 4.6.) Let us denote such a ket
, respectively. (See Section 4.6.) Let us denote such a ket
![]() , and let its
energy be
, and let its
energy be ![]() . According to Equation (7.32), the change in this
energy induced by a small external electric field (i.e., small compared to the typical electric field internal to the atom) is given by
. According to Equation (7.32), the change in this
energy induced by a small external electric field (i.e., small compared to the typical electric field internal to the atom) is given by
![]() . We have
. We have
![\begin{multline}
\left[l^{\,2}\, (l+1)^2 - 2\, l\,(l+1)\,l'\,(l'+1) + l'^{\,2}\,...
...,(l'+1)\right] \langle n,l,m\vert\,z\,\vert n',l',m' \rangle = 0,
\end{multline}](img1835.png)
![]() and
and ![]() to Equation (7.40) yields
to Equation (7.40) yields

![]() , of an atom is defined in terms
of the electric-field-induced energy-shift of a given atomic state as follows [67]:
, of an atom is defined in terms
of the electric-field-induced energy-shift of a given atomic state as follows [67]: