


Next: Quadratic Stark Effect
Up: Time-Independent Perturbation Theory
Previous: Two-State System
Non-Degenerate Perturbation Theory
Let us now generalize our perturbation analysis to deal with systems
possessing more than two energy eigenstates. The energy eigenstates of the
unperturbed Hamiltonian,  , are denoted
, are denoted
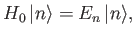 |
(7.19) |
where  runs from 1 to
runs from 1 to 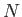 . The eigenkets
. The eigenkets 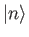 are orthonormal, and
form a complete set.
Let us now try to solve the energy eigenvalue
problem for the perturbed Hamiltonian:
are orthonormal, and
form a complete set.
Let us now try to solve the energy eigenvalue
problem for the perturbed Hamiltonian:
 |
(7.20) |
We can express  as a linear superposition of the unperturbed energy
eigenkets,
as a linear superposition of the unperturbed energy
eigenkets,
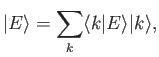 |
(7.21) |
where the summation is from 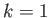 to
to 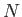 . Substituting the previous
equation into Equation (7.20), and right-multiplying by
. Substituting the previous
equation into Equation (7.20), and right-multiplying by
 , we obtain
, we obtain
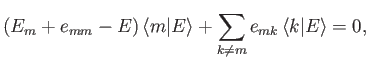 |
(7.22) |
where
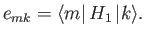 |
(7.23) |
Let us now develop our perturbation expansion. We assume that
 |
(7.24) |
for all 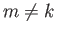 , where
, where
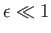 is our expansion parameter. We also
assume that
is our expansion parameter. We also
assume that
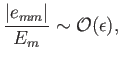 |
(7.25) |
for all  . Let us search for a modified version of the
. Let us search for a modified version of the  th unperturbed energy
eigenstate for which
th unperturbed energy
eigenstate for which
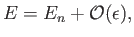 |
(7.26) |
and
for 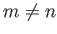 . Suppose that we
write out Equation (7.22) for
. Suppose that we
write out Equation (7.22) for 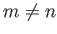 , neglecting terms that
are
, neglecting terms that
are
 according to our expansion scheme. We find that
according to our expansion scheme. We find that
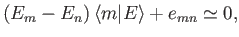 |
(7.29) |
giving
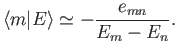 |
(7.30) |
Substituting the previous expression into Equation (7.22),
evaluated for 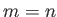 , and neglecting
, and neglecting
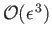 terms, we obtain
terms, we obtain
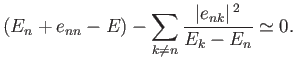 |
(7.31) |
Thus, the modified  th energy eigenstate possesses the eigenvalue
th energy eigenstate possesses the eigenvalue
 |
(7.32) |
and the eigenket
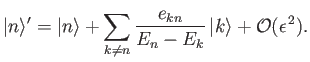 |
(7.33) |
Note that
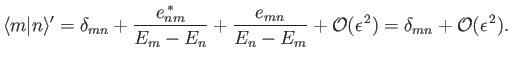 |
(7.34) |
Thus, the modified eigenkets remain orthonormal
to
 .
.
Note, finally, that if the perturbing Hamiltonian, 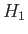 , commutes with the unperturbed Hamiltonian,
, commutes with the unperturbed Hamiltonian,
 , then
, then
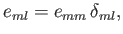 |
(7.35) |
and
The previous two equations are exact (i.e., they hold to all orders in  ).
).



Next: Quadratic Stark Effect
Up: Time-Independent Perturbation Theory
Previous: Two-State System
Richard Fitzpatrick
2016-01-22
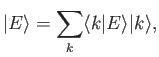

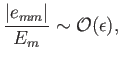
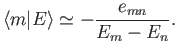
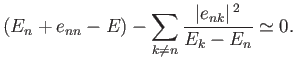
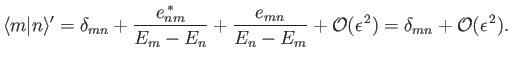
![]() , commutes with the unperturbed Hamiltonian,
, commutes with the unperturbed Hamiltonian,
![]() , then
, then