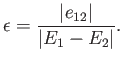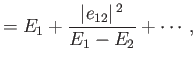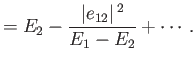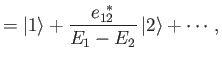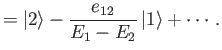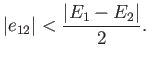Next: Non-Degenerate Perturbation Theory
Up: Time-Independent Perturbation Theory
Previous: Introduction
Two-State System
Consider the simplest non-trivial system, in which there are only two
independent eigenkets of the unperturbed Hamiltonian. These are denoted
It is assumed that these states, and their associated eigenvalues, are known.
Because  is, by definition, an Hermitian operator,
its two eigenkets are mutually orthogonal
and form a complete set. The lengths of these
eigenkets are both normalized to unity.
Let us now try to solve the modified energy eigenvalue problem
is, by definition, an Hermitian operator,
its two eigenkets are mutually orthogonal
and form a complete set. The lengths of these
eigenkets are both normalized to unity.
Let us now try to solve the modified energy eigenvalue problem
 |
(7.4) |
In fact, we can solve this problem exactly. Because the eigenkets of  form a
complete set, we can write
form a
complete set, we can write
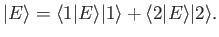 |
(7.5) |
Substituting the previous expansion into Equation (7.4), and then right-multiplying by either
 or
or
 , we get two
coupled equations that can be written in matrix form:
, we get two
coupled equations that can be written in matrix form:
 |
(7.6) |
Here,
are the so-called matrix elements of the perturbing Hamiltonian (with respect to the unperturbed eigenstates).
In the special (but common) case of a perturbing Hamiltonian whose diagonal
matrix elements are zero, so that
 |
(7.10) |
the non-trivial solution of Equation (7.6) (obtained by setting the determinant of the matrix
equal to zero [92]) is
 |
(7.11) |
Let us expand in the supposedly small parameter
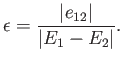 |
(7.12) |
We obtain
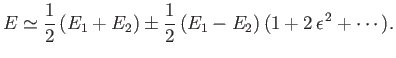 |
(7.13) |
The previous expression yields the modifications to the energy eigenvalues caused by
the perturbing Hamiltonian:
Note that 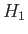 causes the upper eigenvalue to increase, and the lower
eigenvalue to decrease. It is easily demonstrated that the modified eigenkets
take the form
causes the upper eigenvalue to increase, and the lower
eigenvalue to decrease. It is easily demonstrated that the modified eigenkets
take the form
Thus, the modified energy eigenstates consist of one of the unperturbed eigenstates
with a slight admixture of the other. Actually, the series expansion on the right-hand side of Equation (7.13)
only converges when
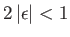 [59]. This suggests that the condition for the
validity of the perturbation expansion is
[59]. This suggests that the condition for the
validity of the perturbation expansion is
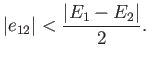 |
(7.18) |
In other words, when we say that 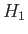 must be small compared to
must be small compared to  ,
what we really mean is that the previous inequality needs to be satisfied.
,
what we really mean is that the previous inequality needs to be satisfied.



Next: Non-Degenerate Perturbation Theory
Up: Time-Independent Perturbation Theory
Previous: Introduction
Richard Fitzpatrick
2016-01-22