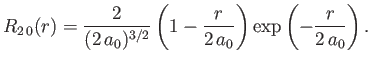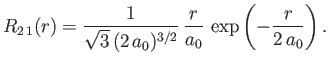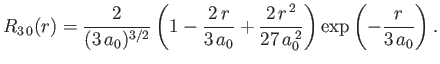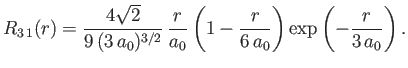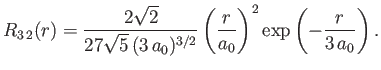Next: Spin Angular Momentum
Up: Orbital Angular Momentum
Previous: Energy Levels of Hydrogen
- Demonstrate directly from the fundamental commutation relations for angular momentum, (4.11), that
(a)
![$ [L^2, L_z] = 0$](img1217.png) , (b)
, (b)
![$ [L^\pm, L_z] = \mp \,\hbar\,L^\pm$](img1218.png) , and (c)
, and (c)
![$ [L^+,L^-] = 2\,\hbar\,L_z$](img1219.png) .
.
- Demonstrate from Equations (4.74)-(4.79) that
where 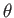 ,
, 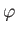 are conventional spherical angles. In addition, show that
are conventional spherical angles. In addition, show that
- A system is in the state
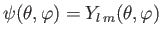 . Evaluate
. Evaluate
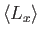 ,
,
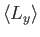 ,
,
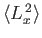 , and
, and
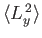 .
.
- Derive Equations (4.108) and (4.109) from Equation (4.107).
- Find the eigenvalues and eigenfunctions (in terms of the angles
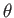 and
and 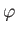 ) of
) of 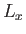 .
Express the
.
Express the 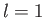 eigenfunctions in terms of the spherical harmonics.
eigenfunctions in terms of the spherical harmonics.
- Consider a beam of particles with
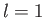 . A measurement of
. A measurement of 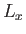 yields the result
yields the result 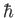 . What
values will be obtained by a subsequent measurement of
. What
values will be obtained by a subsequent measurement of  , and with what probabilities? Repeat
the calculation for the cases in which the measurement of
, and with what probabilities? Repeat
the calculation for the cases in which the measurement of 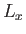 yields the results 0
and
yields the results 0
and
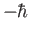 .
.
- The Hamiltonian for an axially symmetric rotator is given by
where
 and
and 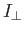 are the moments of inertia about the
are the moments of inertia about the  -axis (which corresponds to the symmetry axis), and about an axis
lying in the
-axis (which corresponds to the symmetry axis), and about an axis
lying in the  -
- plane, respectively.
What are the eigenvalues of
plane, respectively.
What are the eigenvalues of 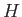 ? [53]
? [53]
- The expectation value of
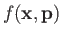 in any stationary state is a constant.
Calculate
in any stationary state is a constant.
Calculate
for a Hamiltonian of the form
Hence, show that
in a stationary state. This is another form of the Virial theorem. (See Exercise 9.)
[53]
- Use the Virial theorem of the previous exercise to prove that
for an energy eigenstate of the hydrogen atom whose principal quantum number is  .
.
- Suppose that a particle's Hamiltonian is
Show that
![$ [{\bf L},p^{\,2}] = {\bf0}$](img1240.png) and
and
![$ [{\bf L},V({\bf x})]=-{\rm i}\,\hbar\,{\bf x}\times \nabla V$](img1241.png) . [Hint: Use the Schrödinger representation.] Hence,
deduce that
. [Hint: Use the Schrödinger representation.] Hence,
deduce that
[Hint: Use the Heisenberg picture.]
Demonstrate that if 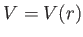 , where
, where
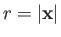 , then
, then
- Let
where  is a non-negative integer.
Show that
is a non-negative integer.
Show that
- Demonstrate that the first few properly normalized radial wavefunctions of the hydrogen atom take the form:
- Demonstrate that
for the hydrogen ground state. In addition, show that
- Show that the most probable value of
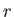 in the hydrogen ground state is
in the hydrogen ground state is 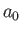 .
.
- Demonstrate that
where
 denotes a properly normalized energy eigenket of the hydrogen atom
corresponding to the standard quantum numbers
denotes a properly normalized energy eigenket of the hydrogen atom
corresponding to the standard quantum numbers  ,
,  , and
, and  .
.
- Let
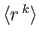 denote the expectation value of
denote the expectation value of 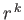 for an energy
eigenstate of the hydrogen atom characterized by the standard quantum numbers
for an energy
eigenstate of the hydrogen atom characterized by the standard quantum numbers  ,
,  , and
, and
 .
.
- Demonstrate that
where
and
 is a well-behaved solution of the differential equation
is a well-behaved solution of the differential equation
- Integrating by parts, show that
and
as well as
- Demonstrate from the governing differential equation for
 that
that
- Combine the final result of part (b) with the governing differential equation to prove that
- Combine the results of parts (c) and (d) to show that
Hence, derive Kramers' relation:
- Use Kramers' relation to prove that
- Let
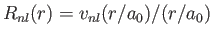 , where
, where 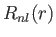 is a properly normalized radial hydrogen wavefunction corresponding to the conventional
quantum numbers
is a properly normalized radial hydrogen wavefunction corresponding to the conventional
quantum numbers  and
and  , and
, and 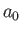 is the Bohr radius.
is the Bohr radius.
- Demonstrate that
- Show that
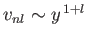 in the limit
in the limit
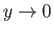 .
.
- Demonstrate that
- Hence, deduce that
for  .
.



Next: Spin Angular Momentum
Up: Orbital Angular Momentum
Previous: Energy Levels of Hydrogen
Richard Fitzpatrick
2016-01-22

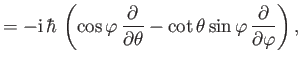


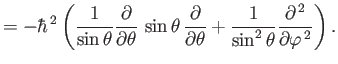
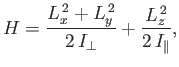
![$\displaystyle 0= \frac{d}{dt}\,(\langle{\bf x}\cdot{\bf p}\rangle) = \frac{{\rm i}}{\hbar}\,\langle[H, {\bf x}\cdot{\bf p}]\rangle
$](img1235.png)

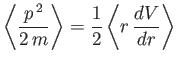
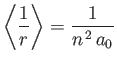
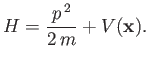
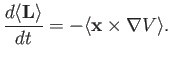
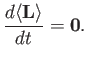
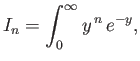
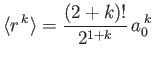
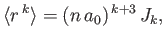
![$\displaystyle J_k = \int_0^\infty dx\,x^{\,k}\,[u(x)]^{\,2},
$](img1262.png)
 is a well-behaved solution of the differential equation
is a well-behaved solution of the differential equation
![$\displaystyle u'' = \left[\frac{l\,(l+1)}{x^{\,2}}-\frac{2\,n}{x}+1\right] u.
$](img1264.png)
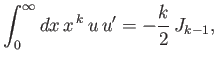
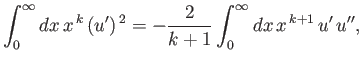
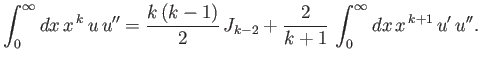
 that
that
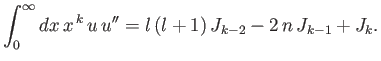
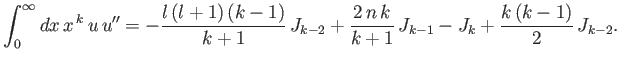
![$\displaystyle \frac{k}{4}\,[(2\,l+1)^2-k^{\,2}]\,J_{k-2} -n\,(2\,k+1)\,J_{k-1}+(k+1)\,J_k = 0.
$](img1270.png)
![$\displaystyle \frac{k\,a_0^{\,2}}{4}\,[(2\,l+1)^2-k^{\,2}]\,\langle r^{\,k-2}\r...
...\,\langle r^{\,k-1}\rangle
+\frac{(k+1)}{n^{\,2}}\,\langle r^{\,k}\rangle = 0.
$](img1271.png)
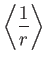
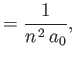
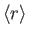
![$\displaystyle = \frac{a_0}{2}\,[3\,n^{\,2}-l\,(l+1)],$](img1275.png)
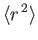
![$\displaystyle = \frac{a_0^{\,2}\,n^{\,2}}{2}\,[5\,n^{\,2}+1-3\,l\,(l+1)].$](img1277.png)
![$\displaystyle \frac{d^{\,2}v_{nl}}{dy^{\,2}} = \left[\frac{l\,(l+1)}{y^{\,2}} -\frac{2}{y} + \frac{1}{n^{\,2}}\right]v_{nl}.
$](img1280.png)
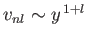 in the limit
in the limit
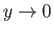 .
.
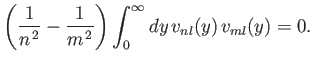
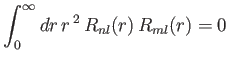
 .
.