


Next: Eigenfunctions of Orbital Angular
Up: Orbital Angular Momentum
Previous: Eigenvalues of Orbital Angular
Rotation Operators
Consider a particle whose position is described by the spherical coordinates
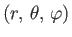 . The classical momentum conjugate to the azimuthal
angle
. The classical momentum conjugate to the azimuthal
angle 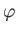 is the
is the  -component of angular momentum,
-component of angular momentum, 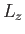 [55].
According to Section 2.5, in quantum mechanics, we can always adopt the Schrödinger
representation, for which ket space is spanned by the simultaneous eigenkets
of the position operators,
[55].
According to Section 2.5, in quantum mechanics, we can always adopt the Schrödinger
representation, for which ket space is spanned by the simultaneous eigenkets
of the position operators, 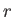 ,
, 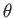 , and
, and 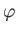 , and
, and 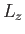 takes the
form
takes the
form
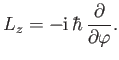 |
(4.57) |
Incidentally, it is legitimate to write the previous equation because there is nothing in Section 2.5 that specifies that
we have to use Cartesian coordinates--the representation (2.74) works for
any well-defined set of coordinates.
Consider an operator
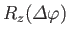 that rotates the system through an angle
that rotates the system through an angle
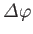 about the
about the 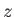 -axis. This operator is very similar to the
operator
-axis. This operator is very similar to the
operator
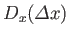 , introduced in Section 2.8, which translates the system
a distance
, introduced in Section 2.8, which translates the system
a distance
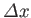 along the
along the  -axis.
We were able to demonstrate in Section 2.8
that
-axis.
We were able to demonstrate in Section 2.8
that
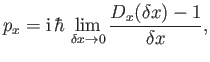 |
(4.58) |
where 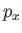 is the linear momentum conjugate to
is the linear momentum conjugate to  . There is nothing
in our derivation of this result that specifies that
. There is nothing
in our derivation of this result that specifies that  has to be a Cartesian
coordinate. Thus, the result should apply just as well to an angular
coordinate. We conclude that
has to be a Cartesian
coordinate. Thus, the result should apply just as well to an angular
coordinate. We conclude that
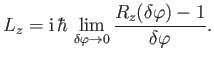 |
(4.59) |
According to Equation (4.59), we can write
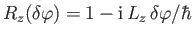 |
(4.60) |
in the limit
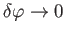 . In other words, the angular momentum
operator
. In other words, the angular momentum
operator 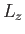 can be used to rotate the system about the
can be used to rotate the system about the 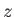 -axis by an infinitesimal amount.
We say that
-axis by an infinitesimal amount.
We say that 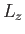 is the generator of rotation about the
is the generator of rotation about the 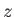 -axis.
The previous equation implies that
-axis.
The previous equation implies that
![$\displaystyle R_z({\mit\Delta}\varphi) = \lim_{N\rightarrow\infty} \left(1-{\rm...
...=0,\infty}\left[\frac{(-{\rm i}\,{\mit\Delta}\varphi\,L_z/\hbar)^n}{n!}\right],$](img1060.png) |
(4.61) |
which reduces to
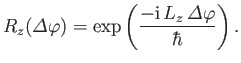 |
(4.62) |
Note that
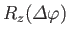 has all of the properties we would expect
a rotation operator to possess: that is,
has all of the properties we would expect
a rotation operator to possess: that is,
(See Exercises 7 and 8.)
Suppose that the system is in a simultaneous eigenstate of 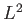 and
and 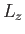 .
As before, this state is represented by the eigenket
.
As before, this state is represented by the eigenket
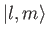 , where
the eigenvalue of
, where
the eigenvalue of 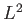 is
is
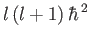 , and
the eigenvalue of
, and
the eigenvalue of 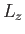 is
is 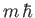 . We expect the wavefunction
to remain unaltered if we rotate
the system
. We expect the wavefunction
to remain unaltered if we rotate
the system 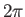 degrees about the
degrees about the 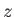 -axis. Thus,
-axis. Thus,
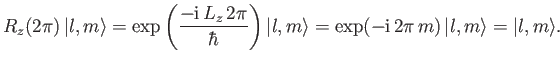 |
(4.66) |
We conclude that 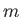 must be an integer. This implies, from the previous
section, that
must be an integer. This implies, from the previous
section, that 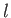 must also be an integer. Thus, an orbital angular momentum
can only take integer values of the quantum numbers
must also be an integer. Thus, an orbital angular momentum
can only take integer values of the quantum numbers 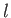 and
and 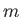 .
.
Consider the action of the rotation operator
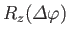 on an eigenstate
possessing zero angular momentum about the
on an eigenstate
possessing zero angular momentum about the 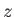 -axis (i.e., an
-axis (i.e., an 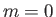 state). We have
state). We have
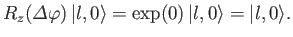 |
(4.67) |
Thus, the eigenstate is invariant to rotations about the 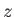 -axis. Clearly,
its wavefunction must be symmetric about the
-axis. Clearly,
its wavefunction must be symmetric about the 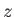 -axis.
-axis.
There is nothing special about the 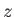 -axis, so we can write
-axis, so we can write
by analogy with Equation (4.62). Here,
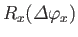 denotes an operator
that rotates the system through an angle
denotes an operator
that rotates the system through an angle
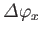 about the
about the  -axis, et cetera.
Suppose that the system is in an eigenstate of zero overall orbital angular momentum
(i.e., an
-axis, et cetera.
Suppose that the system is in an eigenstate of zero overall orbital angular momentum
(i.e., an 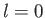 state).
We know that the system is also in an eigenstate of zero orbital angular momentum
about any particular axis. This follows because
state).
We know that the system is also in an eigenstate of zero orbital angular momentum
about any particular axis. This follows because 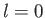 implies
implies 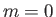 , according
to the
previous section, and we can choose the
, according
to the
previous section, and we can choose the 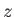 -axis to point in any direction.
Thus,
-axis to point in any direction.
Thus,
Clearly, a zero angular momentum state is invariant to rotations about any
axis.
Such a state must possess a spherically symmetric wavefunction.
Note that, in general, a rotation about the  -axis does not commute with a rotation
about the
-axis does not commute with a rotation
about the 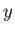 -axis. In other words, if a physical system is rotated through an angle
-axis. In other words, if a physical system is rotated through an angle
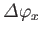 about the
about the  -axis, and then through an angle
-axis, and then through an angle
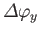 about the
about the
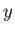 -axis, it ends up in a different state to that obtained by rotating
through an angle
-axis, it ends up in a different state to that obtained by rotating
through an angle
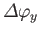 about the
about the
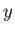 -axis, and then through an angle
-axis, and then through an angle
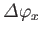 about the
about the  -axis. In quantum
mechanics, this implies that
-axis. In quantum
mechanics, this implies that
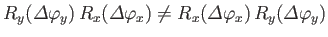 , or
, or
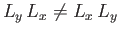 . [See Equations (4.68)-(4.70) and Exercise 3.] Thus, the noncommuting
nature of the angular momentum operators is a direct consequence
of the fact that
rotations do not commute.
. [See Equations (4.68)-(4.70) and Exercise 3.] Thus, the noncommuting
nature of the angular momentum operators is a direct consequence
of the fact that
rotations do not commute.



Next: Eigenfunctions of Orbital Angular
Up: Orbital Angular Momentum
Previous: Eigenvalues of Orbital Angular
Richard Fitzpatrick
2016-01-22
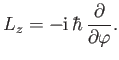
![]() that rotates the system through an angle
that rotates the system through an angle
![]() about the
about the ![]() -axis. This operator is very similar to the
operator
-axis. This operator is very similar to the
operator
![]() , introduced in Section 2.8, which translates the system
a distance
, introduced in Section 2.8, which translates the system
a distance
![]() along the
along the ![]() -axis.
We were able to demonstrate in Section 2.8
that
-axis.
We were able to demonstrate in Section 2.8
that
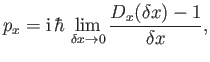
![$\displaystyle R_z({\mit\Delta}\varphi) = \lim_{N\rightarrow\infty} \left(1-{\rm...
...=0,\infty}\left[\frac{(-{\rm i}\,{\mit\Delta}\varphi\,L_z/\hbar)^n}{n!}\right],$](img1060.png)
![]() and
and ![]() .
As before, this state is represented by the eigenket
.
As before, this state is represented by the eigenket
![]() , where
the eigenvalue of
, where
the eigenvalue of ![]() is
is
![]() , and
the eigenvalue of
, and
the eigenvalue of ![]() is
is ![]() . We expect the wavefunction
to remain unaltered if we rotate
the system
. We expect the wavefunction
to remain unaltered if we rotate
the system ![]() degrees about the
degrees about the ![]() -axis. Thus,
-axis. Thus,
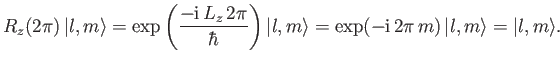
![]() on an eigenstate
possessing zero angular momentum about the
on an eigenstate
possessing zero angular momentum about the ![]() -axis (i.e., an
-axis (i.e., an ![]() state). We have
state). We have
![]() -axis, so we can write
-axis, so we can write
![]() -axis does not commute with a rotation
about the
-axis does not commute with a rotation
about the ![]() -axis. In other words, if a physical system is rotated through an angle
-axis. In other words, if a physical system is rotated through an angle
![]() about the
about the ![]() -axis, and then through an angle
-axis, and then through an angle
![]() about the
about the
![]() -axis, it ends up in a different state to that obtained by rotating
through an angle
-axis, it ends up in a different state to that obtained by rotating
through an angle
![]() about the
about the
![]() -axis, and then through an angle
-axis, and then through an angle
![]() about the
about the ![]() -axis. In quantum
mechanics, this implies that
-axis. In quantum
mechanics, this implies that
![]() , or
, or
![]() . [See Equations (4.68)-(4.70) and Exercise 3.] Thus, the noncommuting
nature of the angular momentum operators is a direct consequence
of the fact that
rotations do not commute.
. [See Equations (4.68)-(4.70) and Exercise 3.] Thus, the noncommuting
nature of the angular momentum operators is a direct consequence
of the fact that
rotations do not commute.