


Next: Fine Structure of Hydrogen
Up: Relativistic Electron Theory
Previous: Electron Spin
To further study the motion of an electron in a central field, whose Hamiltonian is
it is convenient to transform to polar coordinates. Let
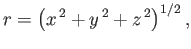 |
(11.129) |
and
 |
(11.130) |
It is easily demonstrated that
![$\displaystyle [r,p_r] = {\rm i} \,\hbar,$](img4045.png) |
(11.131) |
which implies that in the Schrödinger representation
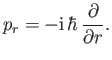 |
(11.132) |
Now, by symmetry, an energy eigenstate in a central field is a simultaneous eigenstate of the total angular momentum
Furthermore, we know from general principles that the eigenvalues of 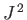 are
are
 , where
, where 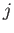 is a positive half-integer (because
is a positive half-integer (because
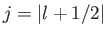 , where
, where  is the standard non-negative integer quantum number associated with orbital angular momentum.)
(See Chapter 6.)
is the standard non-negative integer quantum number associated with orbital angular momentum.)
(See Chapter 6.)
It follows from Equation (11.101) that
However, because 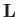 is an angular momentum, its components satisfy the standard commutation relations
is an angular momentum, its components satisfy the standard commutation relations
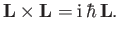 |
(11.135) |
(See Section 4.1.)
Thus, we obtain
However,
 , so
, so
Further application of Equation (11.101) yields
However, it is easily demonstrated from the fundamental commutation relations between position and momentum operators that
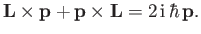 |
(11.140) |
(See Section 2.2.)
Thus,
which implies that
Now,

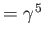
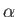 . Moreover,
. Moreover,
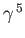 commutes with
commutes with 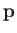 ,
, 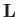 , and
, and
 . Hence,
we conclude that
. Hence,
we conclude that
Finally, because 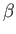 commutes with
commutes with 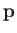 and
and 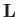 , but anti-commutes with the components of
, but anti-commutes with the components of
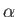 , we obtain
, we obtain
where
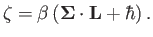 |
(11.145) |
If we repeat the previous analysis, starting at Equation (11.138), but substituting 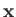 for
for 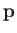 , and
making use of the easily demonstrated result
, and
making use of the easily demonstrated result
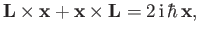 |
(11.146) |
we find that
Now, 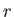 commutes with
commutes with 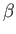 , as well as the components of
, as well as the components of
 and
and 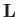 . Hence,
. Hence,
![$\displaystyle [\zeta,r] = 0.$](img4081.png) |
(11.148) |
Moreover, 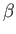 commutes with the components of
commutes with the components of 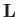 , and can easily be shown to commute with all
of the components of
, and can easily be shown to commute with all
of the components of
 .
It follows that
.
It follows that
![$\displaystyle [\zeta,\beta]=0.$](img4082.png) |
(11.149) |
Hence, Equations (11.128), (11.144), (11.148), and (11.149) imply that
![$\displaystyle [\zeta, H] =0.$](img4083.png) |
(11.150) |
In other words, an eigenstate of the Hamiltonian is a simultaneous eigenstate of 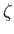 .
Now,
.
Now,
where use has been made of Equation (11.137), as well as
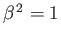 . It follows that the eigenvalues of
. It follows that the eigenvalues of
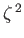 are
are
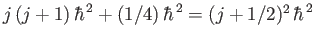 . Thus, the eigenvalues of
. Thus, the eigenvalues of 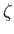 can be written
can be written 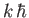 , where
, where
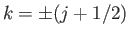 is a non-zero integer.
is a non-zero integer.
Equation (11.101) implies that
where use has been made of Equations (11.130) and (11.145).
It is helpful to define the dimensionless operator  , where
, where
Moreover, it is evident that
![$\displaystyle [\epsilon,r] = 0.$](img4100.png) |
(11.154) |
Hence,
where use has been made of Equation (11.24).
It follows that
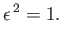 |
(11.156) |
We have already seen that 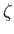 commutes with
commutes with
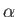
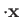 and
and 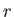 . Thus,
. Thus,
![$\displaystyle [\zeta,\epsilon] = 0.$](img4105.png) |
(11.157) |
Because
 commutes with
commutes with 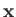 and
and 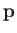 , and
, and
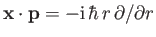 , as well
as
, as well
as
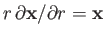 , we obtain
, we obtain
However,
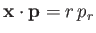 and
and

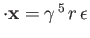 , so, multiplying through by
, so, multiplying through by
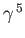 , we get
, we get
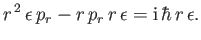 |
(11.159) |
Equation (11.131) then yields
![$\displaystyle [\epsilon,p_r]= 0.$](img4114.png) |
(11.160) |
Equation (11.152) implies that
Making use of Equations (11.148), (11.153), (11.154), and (11.156), we get
  |
(11.162) |
Hence, the Hamiltonian (11.128) becomes
 |
(11.163) |
Now, we wish to solve the energy eigenvalue problem
 |
(11.164) |
where  is the energy eigenvalue. However, we have already shown that an eigenstate of the Hamiltonian is a simultaneous eigenstate of the
is the energy eigenvalue. However, we have already shown that an eigenstate of the Hamiltonian is a simultaneous eigenstate of the 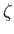 operator belonging to the eigenvalue
operator belonging to the eigenvalue 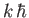 , where
, where 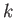 is a non-zero integer. Hence, the eigenvalue problem reduces to
is a non-zero integer. Hence, the eigenvalue problem reduces to
![$\displaystyle \left[- e\,\phi(r) + c\,\epsilon\,(p_r-{\rm i}\,\hbar/r) + {\rm i}\,c\,\hbar\,k\,\epsilon\,\beta/r + \beta\,m_e\,c^{\,2}\right]\psi = E\,\psi,$](img4118.png) |
(11.165) |
which only involves the radial coordinate, 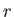 . It is easily demonstrated that
. It is easily demonstrated that  anti-commutes with
anti-commutes with 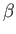 . Hence, given that
. Hence, given that
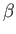 takes the form (11.32), and that
takes the form (11.32), and that
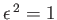 , we can represent
, we can represent  as the matrix
as the matrix
![$\displaystyle \epsilon = \left(\begin{array}{rr}0,&-{\rm i}\\ [0.5ex]{\rm i},&0\end{array}\right).$](img4120.png) |
(11.166) |
Thus, writing 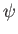 in the spinor form
in the spinor form
![$\displaystyle \psi = \left(\begin{array}{c} \psi_a(r)\\ [0.5ex]\psi_b(r)\end{array}\right),$](img4121.png) |
(11.167) |
and making use of Equation (11.132),
the energy eigenvalue problem for an electron in a central field reduces to the following two coupled radial differential equations:



Next: Fine Structure of Hydrogen
Up: Relativistic Electron Theory
Previous: Electron Spin
Richard Fitzpatrick
2016-01-22

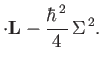
![]() for
for ![]() , and
making use of the easily demonstrated result
, and
making use of the easily demonstrated result
![]() commutes with
commutes with ![]() , as well as the components of
, as well as the components of
![]() and
and ![]() . Hence,
. Hence,
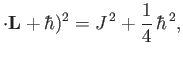
![]() , where
, where
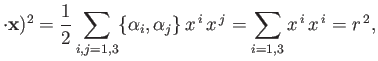
![]() commutes with
commutes with ![]() and
and ![]() , and
, and
![]() , as well
as
, as well
as
![]() , we obtain
, we obtain
![$\displaystyle \epsilon = \left(\begin{array}{rr}0,&-{\rm i}\\ [0.5ex]{\rm i},&0\end{array}\right).$](img4120.png)
![$\displaystyle \psi = \left(\begin{array}{c} \psi_a(r)\\ [0.5ex]\psi_b(r)\end{array}\right),$](img4121.png)