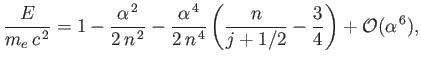Next: Positron Theory
Up: Relativistic Electron Theory
Previous: Motion in Central Field
For the case of a hydrogen atom,
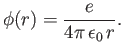 |
(11.170) |
Hence, Equations (11.168) and (11.169) yield
where  , and
, and
with
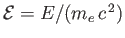 . Here,
. Here,
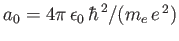 is the Bohr radius, and
is the Bohr radius, and
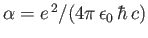 the fine structure constant.
Writing
the fine structure constant.
Writing
where
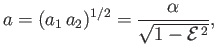 |
(11.177) |
we obtain
Let us search for power-law solutions of the form
where successive values of 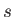 differ by unity. Substitution of these solutions into Equations (11.178) and (11.179) leads to the
recursion relations
differ by unity. Substitution of these solutions into Equations (11.178) and (11.179) leads to the
recursion relations
Multiplying the first of these equations by 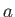 , and the second by
, and the second by 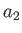 , and then subtracting, we eliminate both
, and then subtracting, we eliminate both 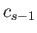 and
and 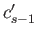 ,
because
,
because
 . We are left with
. We are left with
![$\displaystyle [a\,\alpha-a_2\,(s-k)]\,c_s + [a_2\,\alpha+a\,(s+k)]\,c_{s}' = 0.$](img4149.png) |
(11.184) |
The physical boundary conditions at  require that
require that
 and
and
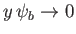 as
as
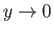 . Thus, it
follows from Equations (11.175) and (11.176) that
. Thus, it
follows from Equations (11.175) and (11.176) that
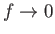 and
and
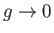 as
as
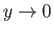 .
Consequently, the series (11.180) and (11.181) must terminate at small positive
.
Consequently, the series (11.180) and (11.181) must terminate at small positive 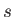 . If
. If 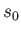 is the minimum value of
is the minimum value of 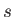 for which
for which  and
and 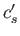 do not both vanish then it follows from Equations (11.182) and (11.183), putting
do not both vanish then it follows from Equations (11.182) and (11.183), putting 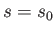 and
and
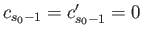 , that
, that
which implies that
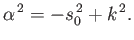 |
(11.187) |
Because the boundary condition requires that the minimum value of 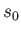 be greater than zero, we must take
be greater than zero, we must take
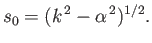 |
(11.188) |
To investigate the convergence of the series (11.180) and (11.181) at large  , we shall determine the
ratio
, we shall determine the
ratio
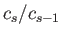 for large
for large  . In the limit of large
. In the limit of large  , Equations (11.183) and (11.184) yield
, Equations (11.183) and (11.184) yield
because
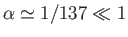 . Thus,
. Thus,
 |
(11.191) |
However, this is the ratio of coefficients in the series expansion of
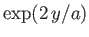 . Hence, we deduce that the series (11.180) and (11.181) diverge
unphysically at large
. Hence, we deduce that the series (11.180) and (11.181) diverge
unphysically at large  unless they terminate at large
unless they terminate at large 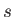 .
.
Suppose that the series (11.180) and (11.181) terminate with the terms  and
and 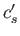 , so that
, so that
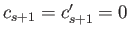 . It
follows from Equations (11.182) and (11.183), with
. It
follows from Equations (11.182) and (11.183), with 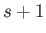 substituted for
substituted for 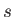 , that
, that
These two expressions are equivalent, because
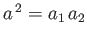 . When combined with Equation (11.184) they give
. When combined with Equation (11.184) they give
![$\displaystyle a_1\left[a\,\alpha-a_2\,(s-k)\right] = a\left[a_2\,\alpha+a\,(s+k)\right],$](img4176.png) |
(11.194) |
which reduces to
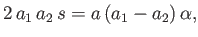 |
(11.195) |
or
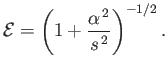 |
(11.196) |
Here, 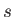 , which specifies the last term in the series, must be greater than
, which specifies the last term in the series, must be greater than 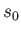 by some non-negative integer
by some non-negative integer 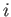 . Thus,
. Thus,
![$\displaystyle s = i+ (k^{\,2}-\alpha^{\,2})^{1/2}= i+\left[(j+1/2)^{\,2}-\alpha^{\,2}\right]^{1/2}.$](img4179.png) |
(11.197) |
where
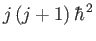 is the eigenvalue of
is the eigenvalue of 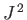 . Hence, the energy eigenvalues of the hydrogen atom become
. Hence, the energy eigenvalues of the hydrogen atom become
![$\displaystyle \frac{E}{m_e\,c^{\,2}} =\left\{1 + \frac{\alpha^{\,2}}{\left(i+[(j+1/2)^{\,2}-\alpha^{\,2}]^{1/2}\right)^2}\right\}^{-1/2}$](img4180.png) |
(11.198) |
[24,57].
Given that
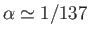 , we can expand the previous expression in
, we can expand the previous expression in
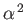 to give
to give
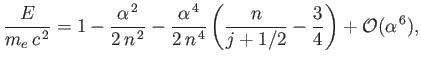 |
(11.199) |
where
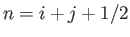 is a positive integer. Of course, the first term in the previous expression corresponds to the electron's
rest mass energy. The second term corresponds to the standard non-relativistic expression for the hydrogen energy levels, with
is a positive integer. Of course, the first term in the previous expression corresponds to the electron's
rest mass energy. The second term corresponds to the standard non-relativistic expression for the hydrogen energy levels, with  playing the role
of the radial quantum number. (See Section 4.6.)
Finally, the third term corresponds to the fine structure correction to these energy levels. (See Exercise 14).
Note that this correction only depends on the quantum numbers
playing the role
of the radial quantum number. (See Section 4.6.)
Finally, the third term corresponds to the fine structure correction to these energy levels. (See Exercise 14).
Note that this correction only depends on the quantum numbers  and
and 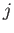 . Now, we showed in Exercise 14 that the fine structure correction to
the energy levels of the hydrogen atom is a combined effect of spin-orbit coupling, the electron's relativistic mass increase,
and the Darwin term. Hence,
it is evident that all of these effects are automatically taken into account in the Dirac equation.
. Now, we showed in Exercise 14 that the fine structure correction to
the energy levels of the hydrogen atom is a combined effect of spin-orbit coupling, the electron's relativistic mass increase,
and the Darwin term. Hence,
it is evident that all of these effects are automatically taken into account in the Dirac equation.



Next: Positron Theory
Up: Relativistic Electron Theory
Previous: Motion in Central Field
Richard Fitzpatrick
2016-01-22
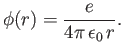
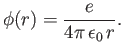
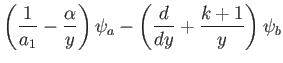
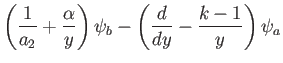
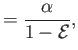

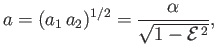
![]() require that
require that
![]() and
and
![]() as
as
![]() . Thus, it
follows from Equations (11.175) and (11.176) that
. Thus, it
follows from Equations (11.175) and (11.176) that
![]() and
and
![]() as
as
![]() .
Consequently, the series (11.180) and (11.181) must terminate at small positive
.
Consequently, the series (11.180) and (11.181) must terminate at small positive ![]() . If
. If ![]() is the minimum value of
is the minimum value of ![]() for which
for which ![]() and
and ![]() do not both vanish then it follows from Equations (11.182) and (11.183), putting
do not both vanish then it follows from Equations (11.182) and (11.183), putting ![]() and
and
![]() , that
, that
![]() , we shall determine the
ratio
, we shall determine the
ratio
![]() for large
for large ![]() . In the limit of large
. In the limit of large ![]() , Equations (11.183) and (11.184) yield
, Equations (11.183) and (11.184) yield
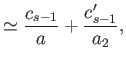

![]() and
and ![]() , so that
, so that
![]() . It
follows from Equations (11.182) and (11.183), with
. It
follows from Equations (11.182) and (11.183), with ![]() substituted for
substituted for ![]() , that
, that

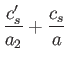
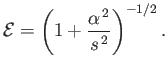
![$\displaystyle \frac{E}{m_e\,c^{\,2}} =\left\{1 + \frac{\alpha^{\,2}}{\left(i+[(j+1/2)^{\,2}-\alpha^{\,2}]^{1/2}\right)^2}\right\}^{-1/2}$](img4180.png)