Next: Exercises
Up: Relativistic Electron Theory
Previous: Fine Structure of Hydrogen
We have already mentioned that the Dirac equation admits twice as many solutions as it ought to, half of them
belonging to states with negative values for the kinetic energy
 . This
difficulty was introduced when we passed from Equation (11.16) to Equation (11.18), and is inherent in any relativistic theory.
. This
difficulty was introduced when we passed from Equation (11.16) to Equation (11.18), and is inherent in any relativistic theory.
Let us examine the negative energy solutions of the equation
a little more closely. For this purpose, it is convenient to use a representation of the 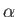 's and
's and 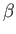 in which all the elements of the matrices
in which all the elements of the matrices 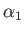 ,
, 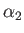 , and
, and  are real, and
all of those of the matrix representing
are real, and
all of those of the matrix representing 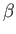 are imaginary or zero. Such a representation can
be obtained from the standard representation by interchanging the expressions for
are imaginary or zero. Such a representation can
be obtained from the standard representation by interchanging the expressions for 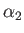 and
and 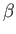 .
If Equation (11.200) is expressed as a matrix equation in this representation, and we then substitute
.
If Equation (11.200) is expressed as a matrix equation in this representation, and we then substitute 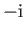 for
for
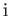 , we get [remembering the factor
, we get [remembering the factor 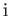 in Equation (11.14)]
in Equation (11.14)]
Thus, each solution, 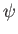 , of the wave equation (11.200) has for its complex conjugate,
, of the wave equation (11.200) has for its complex conjugate, 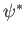 , a solution of the
wave equation (11.201). Furthermore, if the solution,
, a solution of the
wave equation (11.201). Furthermore, if the solution, 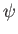 , of Equation (11.200)
belongs to a negative value for
, of Equation (11.200)
belongs to a negative value for
 then the corresponding solution,
then the corresponding solution, 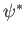 , of Equation (11.201)
will belong to a positive value for
, of Equation (11.201)
will belong to a positive value for
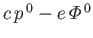 . But, the operator in Equation (11.201) is
just what we would get if we substituted
. But, the operator in Equation (11.201) is
just what we would get if we substituted 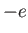 for
for 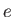 in the operator in Equation (11.200). It follows that each negative
energy solution of Equation (11.200) is the complex conjugate of a positive energy solution of the wave equation
obtained from Equation (11.200) by the substitution of
in the operator in Equation (11.200). It follows that each negative
energy solution of Equation (11.200) is the complex conjugate of a positive energy solution of the wave equation
obtained from Equation (11.200) by the substitution of 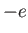 for
for 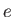 . The latter solution represents an electron
of charge
. The latter solution represents an electron
of charge 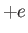 (instead of
(instead of 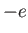 , as we have had up to now) moving through the given electromagnetic field.
, as we have had up to now) moving through the given electromagnetic field.
We conclude that the negative energy solutions of Equation (11.200) refer to the motion of a new type of particle having the
mass of an electron, but the opposite charge [31]. Such particles have been observed experimentally, and are called positrons [3].
Note that we cannot simply assert that the negative energy solutions represent positrons, because this would make the dynamical
relations all wrong. For instance, it is certainly not true that a positron has a negative kinetic energy. Instead, we assume
that nearly all of the negative energy states are occupied, with one electron in each state, in accordance with the Pauli
exclusion principle. An unoccupied negative energy state will now appear as a particle with a positive energy, because to make
it disappear we would have to add an electron with a negative energy to the system. We assume that these unoccupied negative
energy states correspond to positrons.
The previous assumptions require there to be a distribution of electrons of infinite density everywhere in space. A perfect
vacuum is a region of space in which all states of positive energy are unoccupied, and all of those of negative energy are occupied.
In such a vacuum, the Maxwell equation
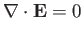 |
(11.200) |
must be valid. This implies that the infinite distribution of negative energy electrons does not contribute to the
electric field. Thus, only departures from the vacuum distribution contribute to the electric charge density 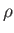 in the
Maxwell equation
in the
Maxwell equation
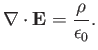 |
(11.201) |
In other words, there is a contribution 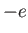 for each occupied state of positive energy, and a contribution
for each occupied state of positive energy, and a contribution 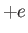 for each unoccupied
state of negative energy.
for each unoccupied
state of negative energy.
The exclusion principle ordinarily prevents a positive energy electron from making transitions to states of negative energy.
However, it is still possible for such an electron to drop into an unoccupied state of negative energy. In this case, we would
observe an electron and a positron simultaneously disappearing, their energy being emitted in the form of radiation. The
converse process would consist in the creation of an electron-positron pair from electromagnetic radiation.



Next: Exercises
Up: Relativistic Electron Theory
Previous: Fine Structure of Hydrogen
Richard Fitzpatrick
2016-01-22
![\begin{multline}
\left[\left(p^{\,0}+\frac{e}{c}\,{\mit\Phi}^{\,0}\right)-\alpha...
...}+\frac{e}{c}\,{\mit\Phi}^{\,3}\right)-\beta\,m_e\,c\right]\psi=0
\end{multline}](img4184.png)