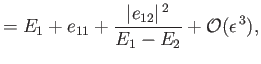 |
||
 |
and
 |
||
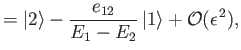 |
respectively. Here,
and
to all orders in the perturbation expansion.
and
respectively, where
![$\displaystyle e^\pm = \frac{1}{2}\,(e_{11}+e_{22})\pm \frac{1}{2}\left[(e_{11}-e_{22})^2+4\,\vert e_{12}\vert^{\,2}\right]^{1/2},
$](img2144.png)
and

Demonstrate that the
is added to
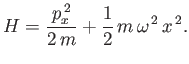
[53]
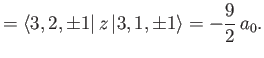 |
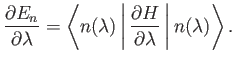
[61]

Moreover, when expressed as a function of
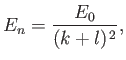
where
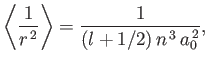
where the expectation value is taken over the energy eigenstate corresponding to the quantum numbers
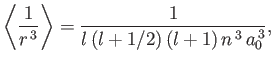
where the expectation value is taken over the energy eigenstate of the hydrogen atom characterized by the standard quantum numbers
Making use of the standard relativistic result [49]
where


where

is the first-order correction due to the electron's relativistic mass increase. (See Exercise 10.) Treating

where
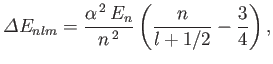
where
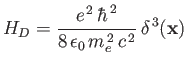
[9]. This correction is usually referred to as the Darwin term [24]. Treating
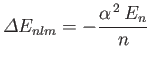
for an
for an
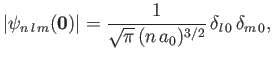
where
![$\displaystyle {\mit\Delta}E_{nlm} = -\frac{\alpha^{\,2}\,E_n}{n^{\,2}}\left[\frac{n}{2\,(l+1/2)\,(l+1)}\right]
$](img2182.png)
for
![$\displaystyle {\mit\Delta}E_{nlm} = \frac{\alpha^{\,2}\,E_n}{n^{\,2}}\left[\frac{n}{2\,(l+1/2)\,l}\right]
$](img2183.png)
for
for the special case of an
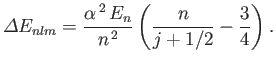
Here,
Show that fine structure causes the
energy of the
![]() states of a hydrogen atom to exceed those of the
states of a hydrogen atom to exceed those of the
![]() and
and
![]() states by
states by
![]() .
.

where the
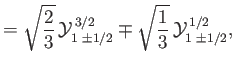 |
||
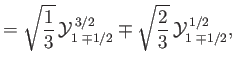 |
||
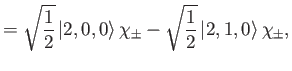 |
||
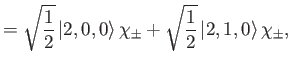 |
||
(See Section 7.6.) Here,
where
where
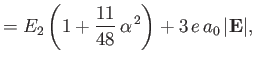 |
||
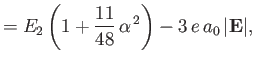 |
||
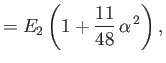 |
||
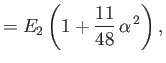 |
||
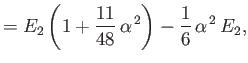 |
||
 |
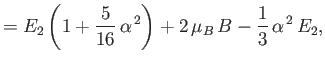 |
||
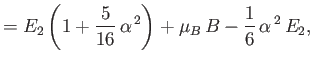 |
||
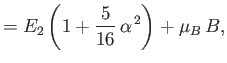 |
||
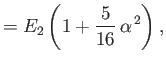 |
||
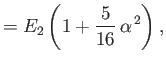 |
||
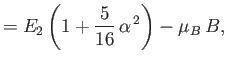 |
||
 |
||
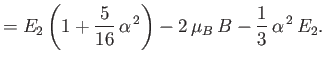 |
Here,