


Next: Wavefunctions
Up: Position and Momentum
Previous: Introduction
Poisson Brackets
Consider a dynamical system whose state at a particular time, 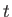 , is
fully specified
by
, is
fully specified
by 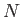 independent classical coordinates
independent classical coordinates 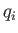 (where
(where 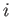 runs from 1 to
runs from 1 to 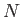 ).
Associated with each generalized coordinate,
).
Associated with each generalized coordinate, 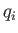 , is a
classical canonical momentum,
, is a
classical canonical momentum,
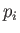 [55]. For instance, a Cartesian coordinate has an associated linear
momentum, an angular coordinate has an associated angular momentum, et cetera [50].
As is well known, the behavior of a classical system can be specified in terms
of either Lagrangian or Hamiltonian dynamics [55]. For instance, in Hamiltonian dynamics,
[55]. For instance, a Cartesian coordinate has an associated linear
momentum, an angular coordinate has an associated angular momentum, et cetera [50].
As is well known, the behavior of a classical system can be specified in terms
of either Lagrangian or Hamiltonian dynamics [55]. For instance, in Hamiltonian dynamics,
where the function
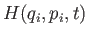 is the system energy at time
is the system energy at time 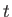 expressed in terms of the
classical coordinates and canonical momenta. This function is
usually referred to as the Hamiltonian of the system [55].
expressed in terms of the
classical coordinates and canonical momenta. This function is
usually referred to as the Hamiltonian of the system [55].
We are interested in
finding some
construct in classical dynamics that consists of
products of dynamical variables. If such a construct exists then we hope to
generalize it somehow to obtain a
rule describing how dynamical variables
commute with one another in quantum mechanics. There is, indeed,
one well-known construct
in classical dynamics that involves products of dynamical variables. The classical
Poisson bracket of two dynamical variables, 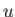 and
and 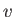 , is defined [55]
, is defined [55]
![$\displaystyle [u, v]_{cl} = \sum_{i=1,N} \left(\frac{\partial u}{\partial q_i}\...
... p_i} - \frac{\partial u}{\partial p_i}\frac{\partial v}{\partial q_i} \right),$](img294.png) |
(2.3) |
where 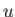 and
and 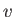 are regarded as functions of the coordinates
and momenta,
are regarded as functions of the coordinates
and momenta, 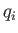 and
and 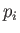 , respectively. It is easily demonstrated that
, respectively. It is easily demonstrated that
(See Exercise 1.)
The time evolution of a dynamical variable can also
be
written in terms of a Poisson bracket by noting that
![$\displaystyle \frac{du}{dt} = \sum_{i=1,N} \left(\frac{\partial u}{\partial q_i...
...c{\partial u}{\partial p_i}\frac{\partial H}{\partial q_i}\right) =[u, H]_{cl},$](img299.png) |
(2.7) |
where use has been made of Hamilton's equations, Equations (2.1)-(2.2).
Let us attempt to construct a quantum mechanical Poisson bracket in which 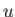 and
and
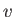 are non-commuting operators instead of functions. Now, the main properties
of the classical Poisson bracket are as follows:
are non-commuting operators instead of functions. Now, the main properties
of the classical Poisson bracket are as follows:
(See Exercise 2.)
The final relation is known as the Jacobi identity. In the previous expressions,
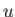 ,
, 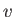 ,
, 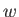 , et cetera, represent dynamical variables, and
, et cetera, represent dynamical variables, and 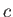 represents a complex number.
We wish to find some combination of non-commuting operators,
represents a complex number.
We wish to find some combination of non-commuting operators, 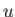 and
and 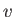 ,
that satisfies Equation (2.8)-(2.14). We shall refer to such a combination as a quantum mechanical Poisson bracket.
,
that satisfies Equation (2.8)-(2.14). We shall refer to such a combination as a quantum mechanical Poisson bracket.
Actually, we can evaluate the quantum mechanical Poisson bracket,
![$ [u_1 \,u_2, v_1 \,v_2]_{qm}$](img314.png) , in
two different ways, because we can employ either of the formulae (2.12) or
(2.13) first. Thus,
, in
two different ways, because we can employ either of the formulae (2.12) or
(2.13) first. Thus,
and
Note that the order of the various factors has been preserved in the previous expressions, because these factors
now represent non-commuting operators. Equating the previous two results
yields
![$\displaystyle [u_1, v_1]_{qm}\, (u_2 \,v_2 - v_2 \,u_2) = (u_1 \,v_1-v_1\, u_1)\,[u_2, v_2]_{qm}.$](img323.png) |
(2.17) |
Because this relation must hold for 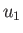 and
and 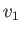 , quite independent of
, quite independent of
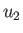 and
and 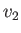 , it follows that
, it follows that
where 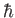 does not depend on
does not depend on 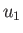 ,
, 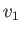 ,
, 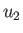 ,
, 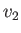 , and also
commutes with
, and also
commutes with
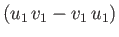 . Because
. Because 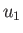 , et cetera, are general
operators, it follows that
, et cetera, are general
operators, it follows that 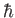 is just a number. Now, we need the quantum
mechanical Poisson
bracket of two Hermitian operators to be itself an Hermitian operator, because
the classical Poisson bracket of two real dynamical variables is real. This
requirement is satisfied if
is just a number. Now, we need the quantum
mechanical Poisson
bracket of two Hermitian operators to be itself an Hermitian operator, because
the classical Poisson bracket of two real dynamical variables is real. This
requirement is satisfied if 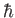 is a real number. Thus, the
quantum mechanical Poisson bracket of two dynamical variables
is a real number. Thus, the
quantum mechanical Poisson bracket of two dynamical variables 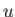 and
and 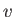 is given by
is given by
![$\displaystyle [u, v]_{qm} = \frac{u\,v - v\,u}{{\rm i} \,\hbar},$](img333.png) |
(2.20) |
where 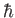 is a new universal constant of nature. Quantum mechanics agrees with
experiments provided that
is a new universal constant of nature. Quantum mechanics agrees with
experiments provided that 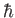 takes the value
takes the value 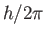 , where
, where
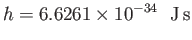 |
(2.21) |
is Planck's constant. (The quantity 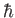 is usually referred to as the
reduced Planck constant.) The notation
is usually referred to as the
reduced Planck constant.) The notation
![$ [u, v]$](img336.png) is
conventionally reserved for the commutator,
is
conventionally reserved for the commutator, 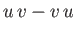 , in quantum mechanics.
Thus,
, in quantum mechanics.
Thus,
![$\displaystyle [u, v]_{qm} = \frac{[u, v]}{{\rm i}\, \hbar}.$](img338.png) |
(2.22) |
It is easily demonstrated that the quantum mechanical Poisson bracket, as defined in the previous equation,
satisfies all of the relations (2.8)-(2.14). (See Exercise 2.)
The strong analogy we have found between the classical Poisson bracket, defined
in Equation (2.3), and the quantum mechanical
Poisson bracket, defined in Equation (2.22), leads
us to assume that the quantum mechanical bracket has the same
value as the corresponding classical bracket, at least for the simplest
cases. In other words, we are going to assume that Equations (2.4)-(2.6) hold for quantum
mechanical, as well as classical, Poisson brackets. This argument yields the
fundamental commutation relations
These results provide us with the basis for calculating commutation
relations between general dynamical variables. For instance, if
two dynamical variables, 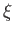 and
and 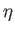 ,
can both be written as a power series in the
,
can both be written as a power series in the
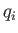 and
and 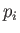 then repeated application of Equations (2.8)-(2.14)
allows
then repeated application of Equations (2.8)-(2.14)
allows
![$ [\xi, \eta]$](img343.png) to be expressed in terms of the fundamental
commutation relations (2.23)-(2.25).
to be expressed in terms of the fundamental
commutation relations (2.23)-(2.25).
Equations (2.23)-(2.25) provide the foundation for the analogy between quantum mechanics
and classical mechanics. Note that the classical result that dynamical variables commute
is obtained in the limit
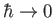 . Thus, classical mechanics
can be regarded as the limiting case of quantum mechanics as
. Thus, classical mechanics
can be regarded as the limiting case of quantum mechanics as
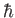 goes to zero.
In classical mechanics, each
generalized coordinate and its conjugate momentum,
goes to zero.
In classical mechanics, each
generalized coordinate and its conjugate momentum, 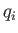 and
and
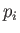 , respectively, correspond to a different classical degree of freedom of the system.
It is clear from Equations (2.23)-(2.25) that, in quantum mechanics, the dynamical
variables corresponding to different degrees of freedom commute.
In fact, it is only those variables corresponding to the same degree of freedom that
may fail to commute.
, respectively, correspond to a different classical degree of freedom of the system.
It is clear from Equations (2.23)-(2.25) that, in quantum mechanics, the dynamical
variables corresponding to different degrees of freedom commute.
In fact, it is only those variables corresponding to the same degree of freedom that
may fail to commute.



Next: Wavefunctions
Up: Position and Momentum
Previous: Introduction
Richard Fitzpatrick
2016-01-22
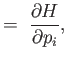
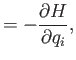
![]() and
and ![]() , is defined [55]
, is defined [55]
![]() and
and
![]() are non-commuting operators instead of functions. Now, the main properties
of the classical Poisson bracket are as follows:
are non-commuting operators instead of functions. Now, the main properties
of the classical Poisson bracket are as follows:
![]() , in
two different ways, because we can employ either of the formulae (2.12) or
(2.13) first. Thus,
, in
two different ways, because we can employ either of the formulae (2.12) or
(2.13) first. Thus,
![$\displaystyle [u, v]_{qm} = \frac{u\,v - v\,u}{{\rm i} \,\hbar},$](img333.png)
![]() . Thus, classical mechanics
can be regarded as the limiting case of quantum mechanics as
. Thus, classical mechanics
can be regarded as the limiting case of quantum mechanics as
![]() goes to zero.
In classical mechanics, each
generalized coordinate and its conjugate momentum,
goes to zero.
In classical mechanics, each
generalized coordinate and its conjugate momentum, ![]() and
and
![]() , respectively, correspond to a different classical degree of freedom of the system.
It is clear from Equations (2.23)-(2.25) that, in quantum mechanics, the dynamical
variables corresponding to different degrees of freedom commute.
In fact, it is only those variables corresponding to the same degree of freedom that
may fail to commute.
, respectively, correspond to a different classical degree of freedom of the system.
It is clear from Equations (2.23)-(2.25) that, in quantum mechanics, the dynamical
variables corresponding to different degrees of freedom commute.
In fact, it is only those variables corresponding to the same degree of freedom that
may fail to commute.