


Next: Exercises
Up: Scattering Theory
Previous: Elastic and Inelastic Scattering
Consider two identical particles that scatter off one another. In the center of mass frame, there is no way of distinguishing a deflection
of a particle through an angle 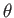 , and a deflection through an angle
, and a deflection through an angle
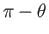 , because momentum conservation demands that if one of the particles is scattered in the direction
characterized by the angle
, because momentum conservation demands that if one of the particles is scattered in the direction
characterized by the angle 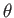 then the other is scattered in the direction characterized by
then the other is scattered in the direction characterized by
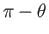 [55].
(Here, for the sake of simplicity, we are assuming that the scattering potential is spherically symmetric, which implies that the motion of the two particles is confined to a fixed plane passing through the origin.)
[55].
(Here, for the sake of simplicity, we are assuming that the scattering potential is spherically symmetric, which implies that the motion of the two particles is confined to a fixed plane passing through the origin.)
In classical mechanics, the differential cross-section for scattering is affected by the identity of the particles because the
number of particles counted by a detector located at angular position 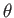 is the sum of the counts due to the two particles, which implies that
is the sum of the counts due to the two particles, which implies that
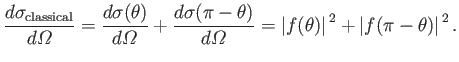 |
(10.158) |
[See Equation (10.28).]
In quantum mechanics, the overall wavefunction must be either symmetric or antisymmetric under interchange of
identical particles, depending on whether the particles in question are bosons or fermions, respectively. (See Section 9.3.)
If the spatial wavefunction is symmetric then Equation (10.55) is replaced by
![$\displaystyle \psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left( {\rm e}^{\,{\rm i}\...
...frac{{\rm e}^{\,{\rm i}\,k\,r}}{r}\left[f(\theta)+f(\pi-\theta)\right] \right),$](img3718.png) |
(10.159) |
and the associated differential scattering cross-section becomes
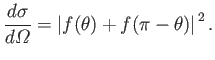 |
(10.160) |
[See Equation (10.28).]
On the other hand, if the spatial wavefunction is antisymmetric then
Equation (10.55) is replaced by
![$\displaystyle \psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left( {\rm e}^{\,{\rm i}\...
...frac{{\rm e}^{\,{\rm i}\,k\,r}}{r}\left[f(\theta)-f(\pi-\theta)\right] \right),$](img3720.png) |
(10.161) |
and the associated differential scattering cross-section is written
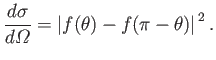 |
(10.162) |
For the case of two identical spin-zero (i.e., boson) particles (e.g., 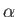 -particles), the spatial wavefunction
is symmetric with respect to particle interchange, which implies that
-particles), the spatial wavefunction
is symmetric with respect to particle interchange, which implies that
The previous result
differs from the classical one because of the interference term (i.e., the final term on the
right-hand side),
which leads to an enhancement of the differential scattering cross-section at
 .
In fact,
.
In fact,
![$\displaystyle \left(\frac{d\sigma}{d{\mit\Omega}} \right)_{\theta=\pi/2}=4\left[f(\pi/2)\right]^{\,2},$](img3726.png) |
(10.164) |
whereas
![$\displaystyle \left(\frac{d\sigma_{\rm classical}}{d{\mit\Omega}} \right)_{\theta=\pi/2}=2\left[f(\pi/2)\right]^{\,2}.$](img3727.png) |
(10.165) |
For the case of two identical spin-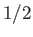 (i.e., fermion) particles (e.g., electrons or protons),
the overall wavefunction is antisymmetric under particle
interchange.
If the two particles are in the spin singlet state (see Section 7.9) then the spatial wavefunction is
symmetric (because the spin wavefunction is antisymmetric), and
(i.e., fermion) particles (e.g., electrons or protons),
the overall wavefunction is antisymmetric under particle
interchange.
If the two particles are in the spin singlet state (see Section 7.9) then the spatial wavefunction is
symmetric (because the spin wavefunction is antisymmetric), and
On the other hand, if the two particles are in the spin triplet state then the spatial
wavefunction is antisymmetric (because the spin wavefunction is symmetric), which leads to
In the former case, the interference term leads to an enhancement (with respect to the classical case) of the differential scattering cross-section at
 : that is,
: that is,
![$\displaystyle \left(\frac{d\sigma_{\rm singlet}}{d{\mit\Omega}} \right)_{\theta=\pi/2}=4\left[f(\pi/2)\right]^{\,2}.$](img3732.png) |
(10.168) |
In the latter case, the interference term leads to the
complete suppression of scattering in the direction
 : that is,
: that is,
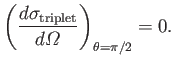 |
(10.169) |
Consider the mutual scattering of two unpolarized beams of spin-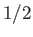 particles. All spin states
are equally likely, so the probability of finding a given pair of particles (one from each beam) in the triplet state is three
times that of finding it in the singlet state (see Section 7.9), which implies that
particles. All spin states
are equally likely, so the probability of finding a given pair of particles (one from each beam) in the triplet state is three
times that of finding it in the singlet state (see Section 7.9), which implies that
In this case, the interference term leads to incomplete suppression (with respect to the classical case) of the differential scattering cross-section at
 : that is,
: that is,
![$\displaystyle \left(\frac{d\sigma_{\rm unpolarized}}{d{\mit\Omega}} \right)_{\theta=\pi/2}=\left[f(\pi/2)\right]^{\,2}.$](img3737.png) |
(10.171) |



Next: Exercises
Up: Scattering Theory
Previous: Elastic and Inelastic Scattering
Richard Fitzpatrick
2016-01-22
![]() is the sum of the counts due to the two particles, which implies that
is the sum of the counts due to the two particles, which implies that
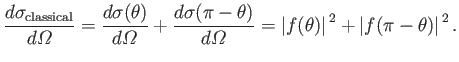
![$\displaystyle \psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left( {\rm e}^{\,{\rm i}\...
...frac{{\rm e}^{\,{\rm i}\,k\,r}}{r}\left[f(\theta)+f(\pi-\theta)\right] \right),$](img3718.png)
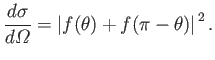
![$\displaystyle \psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left( {\rm e}^{\,{\rm i}\...
...frac{{\rm e}^{\,{\rm i}\,k\,r}}{r}\left[f(\theta)-f(\pi-\theta)\right] \right),$](img3720.png)
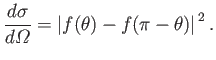
![]() -particles), the spatial wavefunction
is symmetric with respect to particle interchange, which implies that
-particles), the spatial wavefunction
is symmetric with respect to particle interchange, which implies that
![$\displaystyle \left(\frac{d\sigma}{d{\mit\Omega}} \right)_{\theta=\pi/2}=4\left[f(\pi/2)\right]^{\,2},$](img3726.png)
![$\displaystyle \left(\frac{d\sigma_{\rm classical}}{d{\mit\Omega}} \right)_{\theta=\pi/2}=2\left[f(\pi/2)\right]^{\,2}.$](img3727.png)
![]() (i.e., fermion) particles (e.g., electrons or protons),
the overall wavefunction is antisymmetric under particle
interchange.
If the two particles are in the spin singlet state (see Section 7.9) then the spatial wavefunction is
symmetric (because the spin wavefunction is antisymmetric), and
(i.e., fermion) particles (e.g., electrons or protons),
the overall wavefunction is antisymmetric under particle
interchange.
If the two particles are in the spin singlet state (see Section 7.9) then the spatial wavefunction is
symmetric (because the spin wavefunction is antisymmetric), and

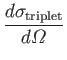
![$\displaystyle \left(\frac{d\sigma_{\rm singlet}}{d{\mit\Omega}} \right)_{\theta=\pi/2}=4\left[f(\pi/2)\right]^{\,2}.$](img3732.png)
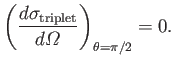
![$\displaystyle \left(\frac{d\sigma_{\rm unpolarized}}{d{\mit\Omega}} \right)_{\theta=\pi/2}=\left[f(\pi/2)\right]^{\,2}.$](img3737.png)