- Assuming, as seems reasonable, that
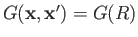 , where
, where
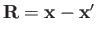 , demonstrate that
the two independent solutions in the region
, demonstrate that
the two independent solutions in the region 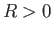 are
are
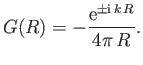
- Show that
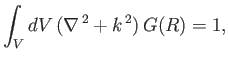
where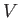 is a sphere of vanishing radius centered on
is a sphere of vanishing radius centered on 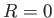 . Hence, deduce that
. Hence, deduce that 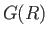 is the required Green's
function.
is the required Green's
function.
- Demonstrate that
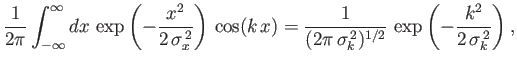
where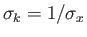 .
.
- Show that
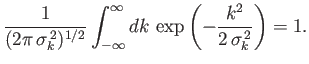
- Finally, by taking the limit
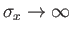 , conclude that
, conclude that
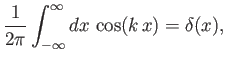
where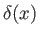 is a Dirac delta function.
is a Dirac delta function.
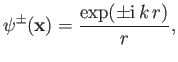
where
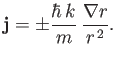
Hence, deduce that
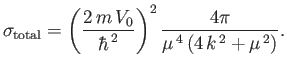
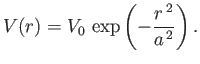
Demonstrate, using the Born approximation, that
![$\displaystyle \frac{ d\sigma}{d{\mit\Omega}}=\left(\frac{\sqrt{\pi}\,m\,V_0\,a^{\,3}}{2\,\hbar^{\,2}}\right)^2\exp\left[-2\,(k\,a)^2\,\sin^2(\theta/2)\right],
$](img3756.png)
and
![$\displaystyle \sigma_{\rm total}= \left(\frac{\sqrt{\pi}\,m\,V_0\,a^{\,3}}{2\,\...
...}\right)^2 2\pi\left[\frac{1-{\rm e}^{-2\,(k\,a)^{\,2}}}{(k\,a)^{\,2}}\right].
$](img3757.png)
![$\displaystyle \frac{d\sigma}{d{\mit\Omega}} = \left(\frac{2\,m_e\,e^{\,2}}{4\pi...
...^{\,2}\,q^{\,2}}\right)^2\left(1-\frac{16}{[4+(q\,a_0)^{\,2}]^{\,2}}\right)^2,
$](img3758.png)
where
![$\displaystyle \sigma_{\rm total} \simeq \frac{m^{\,2}}{\pi\,\hbar^{\,4}}\int d^...
...\bf x}-{\bf x}'\vert]}{k^{\,2}\,\vert{\bf x}-{\bf x}'\vert^{\,2}}\,V(r)\,V(r')
$](img3760.png)
in each of the following ways:
- By directly integrating the differential scattering cross-section obtained from the Born approximation.
- By utilizing the optical theorem in combination with the first two terms in the Born expansion.
[Note that the first term in this expansion is real, and, therefore, does not contribute to
 .]
.]
![$\displaystyle \frac{d\sigma}{d{\mit\Omega}}=\left(\frac{4}{9}\right)\left(\frac...
...ght)\left[1+\frac{2}{5}\,(k\,R)^{\,2}\,\cos\theta+{\cal O}(k\,R)^{\,4}\right],
$](img3766.png)
and
![$\displaystyle \sigma_{\rm total} = \left(\frac{16\,\pi}{9}\right)\left(\frac{m^{\,2}\,V_0^{\,2}\,R^{\,6}}{\hbar^4}\right)\left[1+{\cal O}(k\,R)^{\,4}\right].
$](img3767.png)
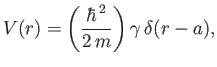
where
![$\displaystyle \delta_0 = -k\,a + \tan^{-1}\left[\frac{1}{\cot(k\,a)+\gamma/k}\right].
$](img3770.png)
Assuming that
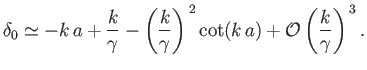
Of course, in the limit
The previous solution breaks down when
![]() , where
, where ![]() is a positive integer.
Suppose that
is a positive integer.
Suppose that
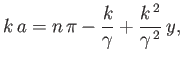
where
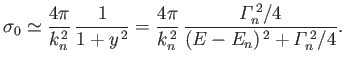
where
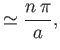 |
||
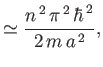 |
||
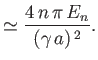 |
Hence, deduce that the net S-wave contribution to the total scattering cross-section is
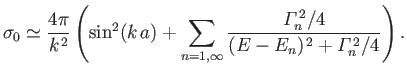
Obviously, there are resonant contributions to the cross-section whenever
![]() .
Note that the
.
Note that the ![]() are the possible energies of particles trapped within the
are the possible energies of particles trapped within the ![]() -shell
potential. Hence, the resonances are clearly associated with incident particles tunneling though the
-shell
potential. Hence, the resonances are clearly associated with incident particles tunneling though the ![]() -shell
and forming transient trapped states. However, the width of the resonances (in energy) decreases strongly as the strength,
-shell
and forming transient trapped states. However, the width of the resonances (in energy) decreases strongly as the strength, ![]() , of the
shell increases.
, of the
shell increases.
![$\displaystyle \frac{d\sigma}{d{\mit\Omega}}\simeq \left(\frac{m_p\,e^{\,2}}{16\...
...frac{1}{\cos^4(\theta/2)}-\frac{1}{\sin^2(\theta/2)\,\cos^2(\theta/2)}\right],
$](img3788.png)
where