Next: Plasma Rotation Up: Linear Resonant Response Model Previous: Response Regimes in Tokamak Contents
 limit, the solution to this equation takes the form
[See Equation (5.83).] In the large-
limit, the solution to this equation takes the form
[See Equation (5.83).] In the large- limit, Equations (5.78)–(5.81) reduce to
This is a parabolic cylinder equation [1] whose most general large-
limit, Equations (5.78)–(5.81) reduce to
This is a parabolic cylinder equation [1] whose most general large- solution is
where
solution is
where  and
and 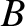 are arbitrary constants,
and
are arbitrary constants,
and
![$\displaystyle \alpha =\left[\frac{P_\perp}{(1+1/\tau)\,D^2}\right]^{1/2}.$](img2301.png) |
(5.118) |
 . Hence, we
must select
. Hence, we
must select 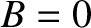 in Equation (5.117), which implies that
at large
in Equation (5.117), which implies that
at large  .
.
![\includegraphics[width=1.\textwidth]{Chapter05/Figure5_5.eps}](img2304.png)
|
Let us make use of the so-called Riccati transformation [5,18],
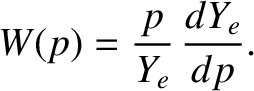 |
(5.120) |
 behavior of the solution to the previous equation is
Likewise, according to Equation (5.119), the large-
behavior of the solution to the previous equation is
Likewise, according to Equation (5.119), the large- behavior of the solution is
Equation (5.121) is conveniently solved numerically by launching a solution of the form (5.123) at large
behavior of the solution is
Equation (5.121) is conveniently solved numerically by launching a solution of the form (5.123) at large  , and then
integrating backward to small
, and then
integrating backward to small  [18]. Equation (5.122) yields
[18]. Equation (5.122) yields
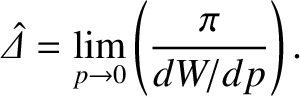 |
(5.124) |
Figure 5.5 shows a numerical solution of the resonant layer equation for a low-field tokamak
fusion reactor. This calculation is made with
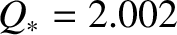 ,
, 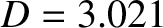 ,
,
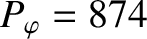 ,
,
 , and
, and 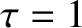 , assuming that
, assuming that  is real. (See Table 5.1.) Note that
is real. (See Table 5.1.) Note that
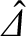 parameterizes the amplitude and phase of
a shielding current that is driven inductively at the rational surface, in response to a rotating tearing perturbation in the
outer region, and acts to suppress magnetic reconnection at the surface [11]. It can be seen that
the shielding current is zero when
parameterizes the amplitude and phase of
a shielding current that is driven inductively at the rational surface, in response to a rotating tearing perturbation in the
outer region, and acts to suppress magnetic reconnection at the surface [11]. It can be seen that
the shielding current is zero when  , which is equivalent to
, which is equivalent to
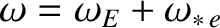 . In other words, the shielding current is zero when the tearing perturbation in the outer region
rotates at the frequency of a naturally unstable tearing mode at the rational surface [2,11]. (See Chapter 6.) The shielding
current clearly increases linearly with
. In other words, the shielding current is zero when the tearing perturbation in the outer region
rotates at the frequency of a naturally unstable tearing mode at the rational surface [2,11]. (See Chapter 6.) The shielding
current clearly increases linearly with 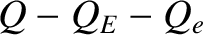 when
when
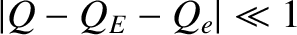 , but saturates in magnitude as
, but saturates in magnitude as
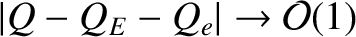 .
.
![\includegraphics[width=1.\textwidth]{Chapter05/Figure5_6.eps}](img2318.png)
|
Figure 5.6 shows a numerical solution of the resonant layer equation for a high-field tokamak
fusion reactor. This calculation is made with
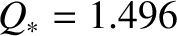 ,
, 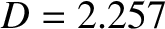 ,
,
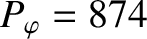 ,
,
 , and
, and 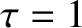 , assuming that
, assuming that  is real. (See Table 5.1.) Note that the figure is very similar to Figure 5.5, indicating that the resonant layer responses in low-field and high-field tokamak fusion reactors do not differ substantially from one another.
is real. (See Table 5.1.) Note that the figure is very similar to Figure 5.5, indicating that the resonant layer responses in low-field and high-field tokamak fusion reactors do not differ substantially from one another.