Next: Magnetic Reconnection Up: Magnetohydrodynamic Fluids Previous: Oblique MHD Shocks Contents
 , where
, where 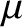 is the dynamic viscosity, so that
is the dynamic viscosity, so that
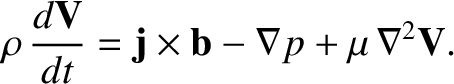
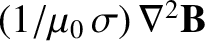 , to give
, to give
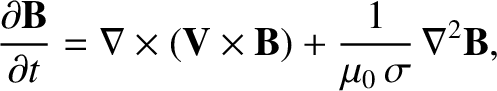
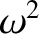 and
and 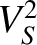 by a
factor
by a
factor
![$\displaystyle [1+{\rm i}\,k^{2}/(\mu_0\,\sigma\,\omega)],$](img3206.png)
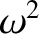 by an additional factor
by an additional factor
![$\displaystyle [1+{\rm i}\,\mu\,k^{2}/(\rho_0\,\omega)].$](img3207.png)
If the finite conductivity and viscous corrections are small (i.e.,
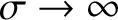 and
and
 ), show that, for
parallel (
), show that, for
parallel (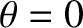 ) propagation, the
dispersion relation for the shear-Alfvén wave reduces to
) propagation, the
dispersion relation for the shear-Alfvén wave reduces to
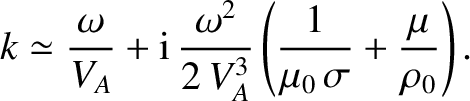
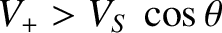 , and
, and
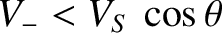 , where
, where 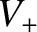 and
and 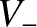 are defined in Equation (8.45).
are defined in Equation (8.45).
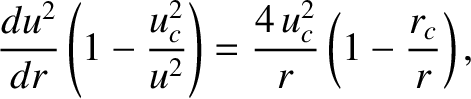
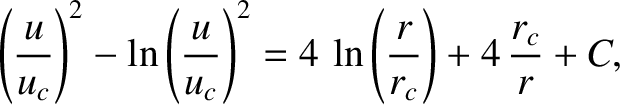
 is a constant.
is a constant.
Let
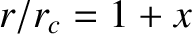 . Demonstrate that, in the limit
. Demonstrate that, in the limit 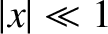 , the previous expression yields either
, the previous expression yields either
![$\displaystyle u^2= u_c^{2}\left[1\pm 2\,x + {\cal O}(x^2)\right]
$](img3214.png)
![$\displaystyle u^2 = u_0^{2}\left[1+\frac{2\,u_c^{2}\,x^2}{u_0^{2}-u_c^{2}} + {\cal O}(x^3)\right],
$](img3215.png)
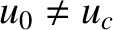 is an arbitrary constant.
Deduce that the former solution with the plus sign is such that
is an arbitrary constant.
Deduce that the former solution with the plus sign is such that 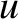 is a monotonically increasing function of
is a monotonically increasing function of 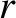 with
with
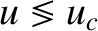 as
as
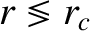 (this is a Class 2 solution); that the former solution with the minus sign is such that
(this is a Class 2 solution); that the former solution with the minus sign is such that 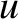 is a monotonically decreasing function of
is a monotonically decreasing function of 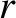 with
with
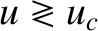 as
as
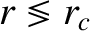 (this is a Class 3 solution); that the latter solution with
(this is a Class 3 solution); that the latter solution with 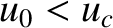 is such that
is such that 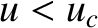 for all
for all 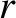 (this is a Class 1 solution);
and that the latter solution with
(this is a Class 1 solution);
and that the latter solution with 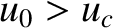 is such that
is such that 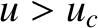 for all
for all 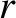 (this is a Class 4 solution).
(this is a Class 4 solution).
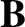 |
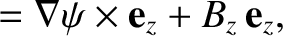 |
|
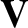 |
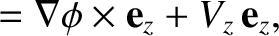 |
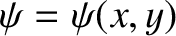 and
and
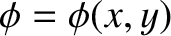 . Here,
. Here,
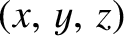 are standard Cartesian coordinates.
Demonstrate from the MHD Ohm's law and Maxwell's equations that
are standard Cartesian coordinates.
Demonstrate from the MHD Ohm's law and Maxwell's equations that
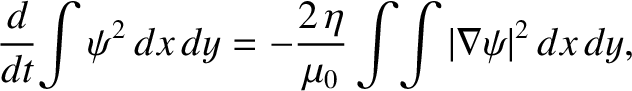
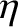 is the (spatially uniform) plasma resistivity. Hence, deduce that a two-dimensional “poloidal” magnetic field,
is the (spatially uniform) plasma resistivity. Hence, deduce that a two-dimensional “poloidal” magnetic field,
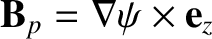 , cannot be maintained against ohmic dissipation by dynamo action.
, cannot be maintained against ohmic dissipation by dynamo action.
Given that
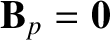 , show that
, show that
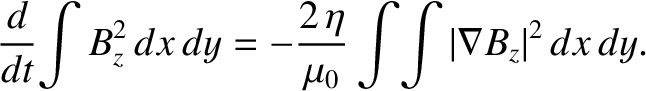
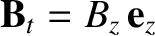 , cannot be maintained against ohmic dissipation by dynamo action.
, cannot be maintained against ohmic dissipation by dynamo action.
![$\displaystyle M_2 = \left[\frac{2+({\mit\Gamma}-1)\,M_1^{2}}{2\,{\mit\Gamma}\,M_1^{2} - ({\mit\Gamma}-1)}\right]^{1/2}.
$](img3233.png)
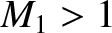 then
then 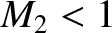 .
.
![$\displaystyle - {\mit\Gamma}\,({\mit\Gamma}+1)\,\beta_2\,M_2^{2}\,r^{2} + {\mit...
...\beta_2)+ ({\mit\Gamma}-1)\,\beta_2\,M_2^{2}\right] r+2\,(2-{\mit\Gamma})\}=0.
$](img3234.png)
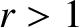 then
then
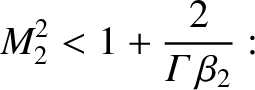
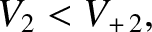
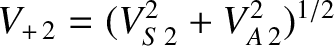 is the downstream fast wave velocity.
is the downstream fast wave velocity.