Next: Exercises Up: Magnetohydrodynamic Fluids Previous: Perpendicular MHD Shocks Contents
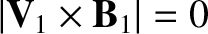 , or
In other words, it is convenient to transform to a frame that moves at the local
, or
In other words, it is convenient to transform to a frame that moves at the local
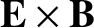 velocity of the plasma.
It immediately follows from the jump condition (8.181) that
or
velocity of the plasma.
It immediately follows from the jump condition (8.181) that
or
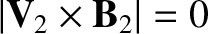 . Thus, in the de Hoffmann-Teller frame, the upstream plasma
flow is parallel to the upstream magnetic field, and the downstream plasma
flow is also parallel to the downstream magnetic field. Furthermore, the magnetic contribution to the jump
condition (8.185) becomes identically zero, which is a considerable simplification.
. Thus, in the de Hoffmann-Teller frame, the upstream plasma
flow is parallel to the upstream magnetic field, and the downstream plasma
flow is also parallel to the downstream magnetic field. Furthermore, the magnetic contribution to the jump
condition (8.185) becomes identically zero, which is a considerable simplification.
Equations (8.208) and (8.209) can be combined with the general jump conditions (8.180)–(8.185) to give
where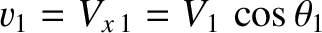 is the component of the upstream velocity normal to the
shock front,
and
is the component of the upstream velocity normal to the
shock front,
and 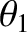 is the angle subtended between the upstream plasma flow and the
shock front normal. Finally, given the compression ratio,
is the angle subtended between the upstream plasma flow and the
shock front normal. Finally, given the compression ratio, 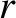 , the square of the normal
upstream velocity,
, the square of the normal
upstream velocity, 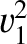 , is a real root of a cubic equation
known as the shock adiabatic:
, is a real root of a cubic equation
known as the shock adiabatic:
| 0 | ![$\displaystyle =(v_{1}^{2}-r\,\cos^2\theta_1\,V_{A\,1}^{2})^{2}\left(
\left[({\mit\Gamma}+1)-({\mit\Gamma}-1)\,r\right]
v_{1}^{2}- 2\,r\,V_{S\,1}^{2}\right)$](img3169.png) |
(8.216) |
![$\displaystyle \phantom{=}-r\,\sin^2\theta_1\,v_{1}^{2}\,V_{A\,1}^{2}\left(
\lef...
...mit\Gamma}+1)-({\mit\Gamma}-1)\,r\right]r\,\cos^2\theta_1\,V_{A\,1}^{2}\right).$](img3170.png) |
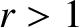 .
.
Let us first consider the weak shock limit
 . In this case, it is easily seen that the three roots of the
shock adiabatic reduce to
. In this case, it is easily seen that the three roots of the
shock adiabatic reduce to
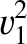 |
![$\displaystyle =V_{-\,1}^{2}\equiv \frac{V_{A\,1}^{2}+V_{S\,1}^{2}- [(V_{A\,1}^{2}+V_{S\,1}^{2})^{2}
-4\,\cos^2\theta_1\,V_{S\,1}^{2}\,V_{A\,1}^{2}]^{1/2}}{2},$](img3173.png) |
(8.217) |
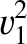 |
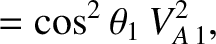 |
(8.218) |
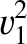 |
![$\displaystyle =V_{+\,1}^{2}\equiv \frac{V_{A\,1}^{2}+V_{S\,1}^{2} + [(V_{A\,1}^{2}+V_{S\,1}^{2})^{2}
-4\,\cos^2\theta_1\,V_{S\,1}^{2}\,V_{A\,1}^{2}]^{1/2}}{2}.$](img3175.png) |
(8.219) |
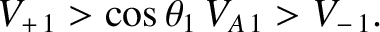 |
(8.220) |
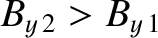 for a fast shock,
whereas
for a fast shock,
whereas
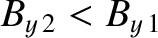 for a slow shock. For the case of an intermediate shock, we
can show, after a little algebra, that
for a slow shock. For the case of an intermediate shock, we
can show, after a little algebra, that
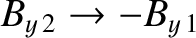 in the limit
in the limit
 . We conclude that (in the de Hoffmann-Teller frame) fast shocks refract the magnetic field and plasma
flow (recall that they are parallel in our adopted frame of the reference) away from
the normal to the shock front, whereas slow shocks refract these quantities toward
the normal. Moreover, the tangential magnetic field and plasma flow generally reverse
across an intermediate shock front. This is illustrated in Figure 8.8.
. We conclude that (in the de Hoffmann-Teller frame) fast shocks refract the magnetic field and plasma
flow (recall that they are parallel in our adopted frame of the reference) away from
the normal to the shock front, whereas slow shocks refract these quantities toward
the normal. Moreover, the tangential magnetic field and plasma flow generally reverse
across an intermediate shock front. This is illustrated in Figure 8.8.
![\includegraphics[height=2.5in]{Chapter08/fig8_8.eps}](img3180.png) |
When 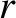 is slightly larger than unity, it is easily demonstrated that the conditions for the
existence of a slow, intermediate, and fast shock are
is slightly larger than unity, it is easily demonstrated that the conditions for the
existence of a slow, intermediate, and fast shock are
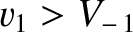 ,
,
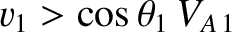 , and
, and
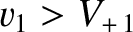 , respectively.
, respectively.
Let us now consider the strong shock limit,
 . In this case, the shock
adiabatic yields
. In this case, the shock
adiabatic yields
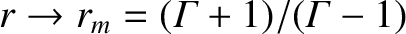 , and
, and
![$\displaystyle v_1^{2} \simeq \frac{r_m}{{\mit\Gamma}-1}\,\frac{2\,V_{S\,1}^{2}+\sin^2\theta_1\,[{\mit\Gamma}
+ (2-{\mit\Gamma})\,r_m]\,V_{A\,1}^{2}}{r_m-r}.$](img3186.png) |
(8.221) |
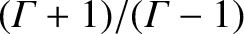 by any type of MHD shock.
by any type of MHD shock.
Consider the special case
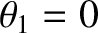 in which both the plasma flow and the
magnetic field are normal to the shock front. In this case, the three roots of the shock adiabatic are
in which both the plasma flow and the
magnetic field are normal to the shock front. In this case, the three roots of the shock adiabatic are
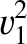 |
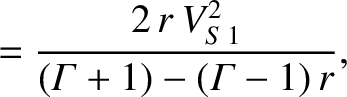 |
(8.222) |
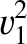 |
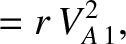 |
(8.223) |
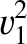 |
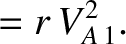 |
(8.224) |
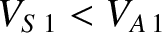 , and as a fast shock
when
, and as a fast shock
when
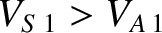 . The other two roots are identical, and correspond to
shocks that propagate at the velocity
. The other two roots are identical, and correspond to
shocks that propagate at the velocity
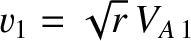 and “switch-on" the tangential
components of the plasma flow and the magnetic field: that is, it can be seen from
Equations (8.212) and (8.214) that
and “switch-on" the tangential
components of the plasma flow and the magnetic field: that is, it can be seen from
Equations (8.212) and (8.214) that
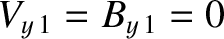 while
while
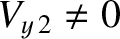 and
and
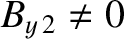 for these types of shock. Incidentally, it is also
possible to have a “switch-off” shock that eliminates the tangential components
of the plasma flow and the magnetic field. According to Equations (8.212) and (8.214),
such a shock propagates at the velocity
for these types of shock. Incidentally, it is also
possible to have a “switch-off” shock that eliminates the tangential components
of the plasma flow and the magnetic field. According to Equations (8.212) and (8.214),
such a shock propagates at the velocity
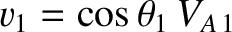 . Switch-on and
switch-off shocks are illustrated in Figure 8.9.
. Switch-on and
switch-off shocks are illustrated in Figure 8.9.
![\includegraphics[height=2.5in]{Chapter08/fig8_9.eps}](img3198.png) |
Let us, finally, consider the special case
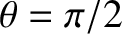 . As is easily demonstrated, the three roots of the
shock adiabatic are
. As is easily demonstrated, the three roots of the
shock adiabatic are
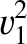 |
![$\displaystyle = r \left(\frac{2\,V_{S\,1}^{2} + [{\mit\Gamma}+(2-{\mit\Gamma})\,r]\,V_{A\,1}^{2}}
{[{\mit\Gamma}+1]-[{\mit\Gamma}-1]\,r}\right)
,$](img3199.png) |
(8.225) |
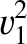 |
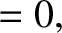 |
(8.226) |
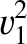 |
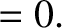 |
(8.227) |
MHD shocks have been observed in a large variety of situations. For instance, shocks are known to be formed by supernova explosions, by strong stellar winds, by solar flares, and by the solar wind upstream of planetary magnetospheres (Gurnett and Bhattacharjee 2005).