Next: Perpendicular MHD Shocks Up: Magnetohydrodynamic Fluids Previous: MHD Shocks Contents
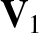 |
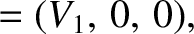 |
 |
 |
(8.186) |
 |
 |
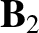 |
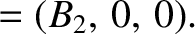 |
(8.187) |
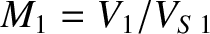 , where
, where
 is the upstream sound speed. Thus, the upstream flow is supersonic if
is the upstream sound speed. Thus, the upstream flow is supersonic if 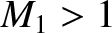 , and subsonic if
, and subsonic if 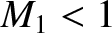 . Incidentally, as is clear from
the previous expressions, a
parallel shock is unaffected by the presence of a magnetic field. In fact, this
type of shock is identical to that which occurs in neutral fluids, and is,
therefore, usually called a hydrodynamic shock (Fitzpatrick 2017).
. Incidentally, as is clear from
the previous expressions, a
parallel shock is unaffected by the presence of a magnetic field. In fact, this
type of shock is identical to that which occurs in neutral fluids, and is,
therefore, usually called a hydrodynamic shock (Fitzpatrick 2017).
It is easily seen from Equations (8.188)–(8.191) that there is no shock (i.e., no jump in plasma parameters across the shock front) when the upstream flow is exactly
sonic: that is, when 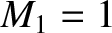 . In other words,
. In other words, 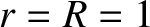 when
when 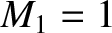 .
However, if
.
However, if  then the upstream
and downstream plasma parameters become different (i.e.,
then the upstream
and downstream plasma parameters become different (i.e., 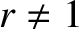 ,
, 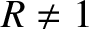 ), and a true shock develops.
In fact, it can be demonstrated that
), and a true shock develops.
In fact, it can be demonstrated that
The previous discussion seems to imply that a parallel shock can be either compressive (i.e., 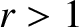 ) or expansive (i.e.,
) or expansive (i.e., 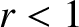 ). However, there is one
additional physics principle that needs to be factored into
our analysis—namely, the second law of thermodynamics. This law states that the entropy of a closed system can spontaneously increase,
but can never spontaneously decrease (Reif 1965). Now, in general, the entropy per particle is different on either side of a hydrodynamic shock front. Accordingly, the second law of thermodynamics
mandates that the downstream entropy must exceed the upstream
entropy, so as to ensure that the shock generates a net increase, rather
than a net decrease, in the overall entropy of the system, as the plasma flows through it.
). However, there is one
additional physics principle that needs to be factored into
our analysis—namely, the second law of thermodynamics. This law states that the entropy of a closed system can spontaneously increase,
but can never spontaneously decrease (Reif 1965). Now, in general, the entropy per particle is different on either side of a hydrodynamic shock front. Accordingly, the second law of thermodynamics
mandates that the downstream entropy must exceed the upstream
entropy, so as to ensure that the shock generates a net increase, rather
than a net decrease, in the overall entropy of the system, as the plasma flows through it.
The (suitably normalized) entropy per particle of an ideal plasma takes the form [see Equation (4.51)]
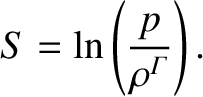 |
(8.195) |
![$\displaystyle [S]^2_1 =\ln R - {\mit\Gamma}\,\ln r.$](img3117.png) |
(8.196) |
![$\displaystyle r\,\frac{d[S]_1^2}{dr} = \frac{r}{R}\,\frac{dR}{dr}-{\mit\Gamma}
...
...({\mit\Gamma}+1)\,r-({\mit\Gamma}-1)]\,[({\mit\Gamma}+1)-({\mit\Gamma}-1)\,r]}.$](img3118.png) |
(8.197) |
![$d[S]_1^2/dr\geq 0$](img3119.png) in all situations of physical interest. However,
in all situations of physical interest. However, ![$[S]_1^2=0$](img3120.png) when
when 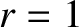 , because, in this case, there is no discontinuity in plasma parameters across the shock front. We conclude that
, because, in this case, there is no discontinuity in plasma parameters across the shock front. We conclude that ![$[S]_1^2<0$](img3122.png) for
for 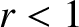 , and
, and
![$[S]_1^2>0$](img3123.png) for
for 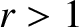 . It follows that the second law of thermodynamics
requires hydrodynamic shocks to be compressive: that is,
. It follows that the second law of thermodynamics
requires hydrodynamic shocks to be compressive: that is, 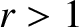 . In other words, the
plasma density must always increase when a shock front
is crossed in the direction of the relative plasma flow. It turns out that this
is a general rule that applies to all three types of MHD shock (Boyd and Sanderson 2003).
. In other words, the
plasma density must always increase when a shock front
is crossed in the direction of the relative plasma flow. It turns out that this
is a general rule that applies to all three types of MHD shock (Boyd and Sanderson 2003).
The upstream Mach number, 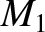 , is a good measure of shock strength:
that is, if
, is a good measure of shock strength:
that is, if 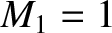 then there is no shock, if
then there is no shock, if
 then the shock is
weak, and if
then the shock is
weak, and if 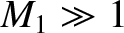 then the shock is strong. We can define an analogous downstream Mach number,
then the shock is strong. We can define an analogous downstream Mach number,
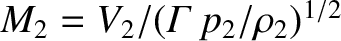 .
It is easily demonstrated from the jump conditions that if
.
It is easily demonstrated from the jump conditions that if 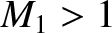 then
then 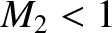 . In other
words, in the shock rest frame, the shock is associated with an irreversible (because the
entropy suddenly increases) transition from supersonic to subsonic flow. Note that
. In other
words, in the shock rest frame, the shock is associated with an irreversible (because the
entropy suddenly increases) transition from supersonic to subsonic flow. Note that
 ,
whereas
,
whereas
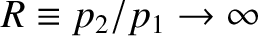 , in the limit
, in the limit
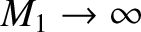 . In other words, as the shock strength increases, the compression ratio,
. In other words, as the shock strength increases, the compression ratio, 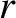 ,
asymptotes to a finite value, whereas the
pressure ratio,
,
asymptotes to a finite value, whereas the
pressure ratio, 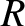 , increases without limit. For a conventional
plasma with
, increases without limit. For a conventional
plasma with
 , the limiting value of the compression ratio is 4: in other words, the downstream density can never be more than four times the upstream density. We conclude that, in the strong shock limit,
, the limiting value of the compression ratio is 4: in other words, the downstream density can never be more than four times the upstream density. We conclude that, in the strong shock limit,
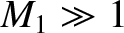 , the
large jump in the plasma pressure across the shock front must be
predominately a consequence of a large jump in the plasma temperature, rather than the plasma density. In fact, Equations (8.190) and (8.191) imply that
, the
large jump in the plasma pressure across the shock front must be
predominately a consequence of a large jump in the plasma temperature, rather than the plasma density. In fact, Equations (8.190) and (8.191) imply that
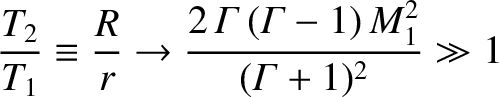 |
(8.198) |
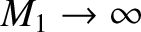 . Thus, a strong parallel, or hydrodynamic, shock
is associated with intense plasma heating.
. Thus, a strong parallel, or hydrodynamic, shock
is associated with intense plasma heating.
As we have seen, the condition for the existence of a hydrodynamic
shock is 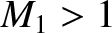 , or
, or
 . In other words, in the
shock frame, the upstream plasma velocity,
. In other words, in the
shock frame, the upstream plasma velocity, 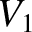 , must be supersonic.
However, by Galilean invariance,
, must be supersonic.
However, by Galilean invariance, 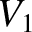 can also be interpreted as the
propagation velocity of the shock through an initially stationary plasma. It follows that, in a stationary plasma,
a parallel, or hydrodynamic, shock propagates along the magnetic field with a supersonic velocity.
can also be interpreted as the
propagation velocity of the shock through an initially stationary plasma. It follows that, in a stationary plasma,
a parallel, or hydrodynamic, shock propagates along the magnetic field with a supersonic velocity.