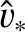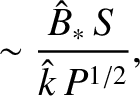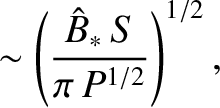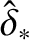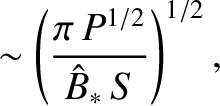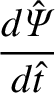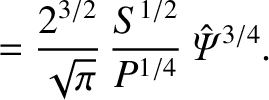- Derive Equations (9.11)–(9.14) from Equations (9.3)–(9.10).
- Consider the linear tearing stability of the following field configuration,
This configuration is generated by a uniform,  -directed current sheet of thickness
-directed current sheet of thickness  , centered at
, centered at 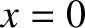 .
.
- Solve the tearing mode equation, (9.31), subject to the constraints
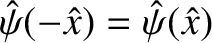 , and
, and
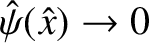 as
as
 . Hence, deduce that the tearing stability index for this configuration is
. Hence, deduce that the tearing stability index for this configuration is
- Show that
as
 , and
, and
as
 .
.
- Demonstrate that the field configuration is tearing unstable (i.e.,
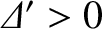 ) provided that
) provided that
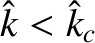 ,
where
,
where
Show that
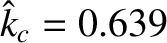 .
.
- We can incorporate plasma viscosity into the reduced-MHD equations, (9.11)–(9.14), by modifying Equation (9.4)
to read
where 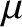 is the viscosity.
is the viscosity.
- Show that the reduced-MHD equations generalize to give
- Show that Equations (9.22) and (9.23) generalize to give
- Show that Equations (9.27) and (9.28) generalize to give
where
is the magnetic Prandtl number, and
is the viscous diffusion time.
- Show that the resistive layer equations, (9.32) and (9.33), generalize to give
- Show that the Fourier transformed resistive layer equation, (9.45), generalizes to give
- Finally, solve the Fourier transformed resistive layer equation to determine the layer matching
parameter,
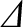 . Demonstrate that if
. Demonstrate that if
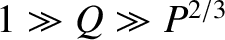 then
then
whereas if
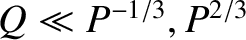 then
then
- Consider the effect of plasma viscosity on the Sweet-Parker reconnection scenario. The viscosity is conveniently parameterized in terms
of the magnetic Prandtl number
where 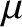 is the viscosity. Demonstrate that if
is the viscosity. Demonstrate that if 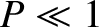 then the conventional Sweet-Parker reconnection scenario remains valid, but that
if
then the conventional Sweet-Parker reconnection scenario remains valid, but that
if 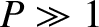 then the scenario is modified such that
then the scenario is modified such that
![$\displaystyle F(\hat{x}) = \left\{\begin{array}{lcl}
F'(0)\,\hat{x}&\mbox{\hspa...
... [0.5ex]
F'(0)\,{\rm sgn}(\hat{x})&&\vert\hat{x}\vert\geq 1\end{array}\right..
$](img3726.png)
 -directed current sheet of thickness
-directed current sheet of thickness 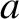 , centered at
, centered at 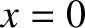 .
.
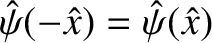 , and
, and
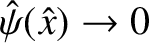 as
as
 . Hence, deduce that the tearing stability index for this configuration is
. Hence, deduce that the tearing stability index for this configuration is
![$\displaystyle {\mit\Delta}' = \frac{2\,\hat{k}}{\tanh\hat{k}}\left[\frac{\hat{k} + \hat{k}\,\tanh\hat{k}-1}{1-\hat{k}/\tanh\hat{k}-\hat{k}}\right].
$](img3729.png)
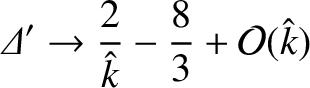
 , and
, and
![$\displaystyle {\mit\Delta}'\rightarrow -2\,\hat{k} + 2\left[1+\frac{1}{2\,\hat{k}}+{\cal O}\left(\frac{1}{\hat{k}^{2}}\right)\right]\exp(-2\,\hat{k})
$](img3731.png)
 .
.
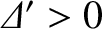 ) provided that
) provided that
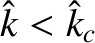 ,
where
,
where
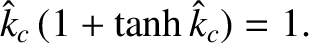
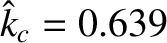 .
.
![$\displaystyle \rho\left[\frac{\partial {\bf V}}{\partial t} + ({\bf V}\cdot\nabla) {\bf V}\right]+\nabla p-{\bf j}\times {\bf B} -\mu\,\nabla^2{\bf V}=0,
$](img3736.png)
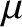 is the viscosity.
is the viscosity.
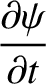
![$\displaystyle = [\phi,\psi]+\frac{\eta}{\mu_0}\,(J-J_0),$](img3264.png)

![$\displaystyle = \rho\,[\phi,U] + \mu_0^{-1}\,[J,\psi]+\mu\,\nabla^2 U,$](img3737.png)
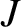

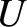
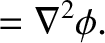
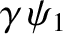
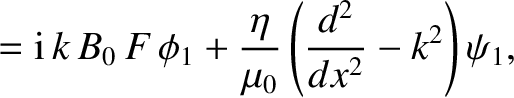
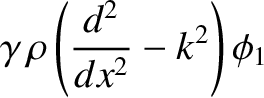
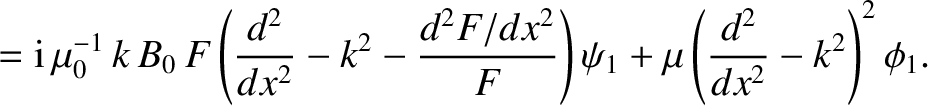
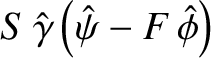

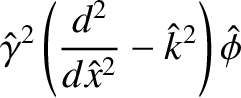
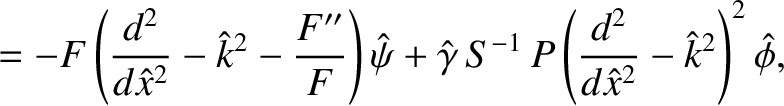
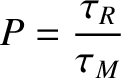
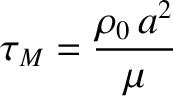
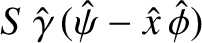
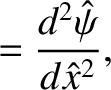


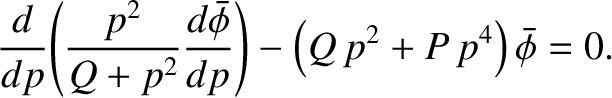
 . Demonstrate that if
. Demonstrate that if
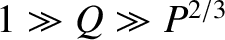 then
then

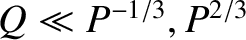 then
then
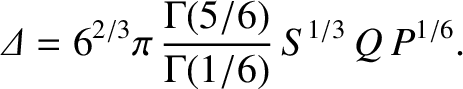
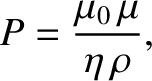
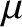 is the viscosity. Demonstrate that if
is the viscosity. Demonstrate that if 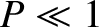 then the conventional Sweet-Parker reconnection scenario remains valid, but that
if
then the conventional Sweet-Parker reconnection scenario remains valid, but that
if 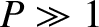 then the scenario is modified such that
then the scenario is modified such that