Next: Asymptotic Matching Up: Magnetic Reconnection Previous: Reduced-MHD Equations Contents
 is a unit vector parallel to the
is a unit vector parallel to the  -axis. The equilibrium plasma flow is assumed to be zero.
The current sheet consists of filaments that run parallel to the
-axis. The equilibrium plasma flow is assumed to be zero.
The current sheet consists of filaments that run parallel to the  -axis. As illustrated in Figure 9.1, the
sheet is centered on the plane
-axis. As illustrated in Figure 9.1, the
sheet is centered on the plane 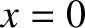 , and is of thickness
, and is of thickness 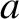 in the
in the  -direction. The magnetic field
generated by the current sheet is parallel to the
-direction. The magnetic field
generated by the current sheet is parallel to the  -axis, of magnitude
-axis, of magnitude 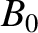 , and switches direction
across the sheet. In other words,
, and switches direction
across the sheet. In other words,
 for
for  , and
, and
 for
for  .
Note that
.
Note that
 at the center of the sheet,
at the center of the sheet, 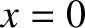 .
.
Consider a small perturbation to the aforementioned current sheet that varies periodically in the  -direction with
wavelength
-direction with
wavelength  . The wavevector of the perturbation is therefore
. The wavevector of the perturbation is therefore
 . It follows that the
perturbation satisfies the shear-Alfvén resonance condition,
. It follows that the
perturbation satisfies the shear-Alfvén resonance condition,
 , at
, at 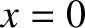 .
We can write
.
We can write
 is the growth-rate of the perturbation, and
is the growth-rate of the perturbation, and  ,
,  ,
,  , and
, and  are all
considered to be small (compared to equilibrium quantities) quantities.
are all
considered to be small (compared to equilibrium quantities) quantities.
Substituting Equations (9.18)–(9.21) into the reduced-MHD equations, (9.11)–(9.14), making use of Equation (9.15), and only retaining terms that are first order in small quantities, we obtain the linearized reduced-MHD equations:
where .
.
It is helpful to define the hydromagnetic timescale,
which is the typical time required for a shear-Alfvén wave to propagate a wavelength parallel to the -axis, as well as the resistive diffusion timescale,
which is the typical time required for magnetic flux to diffuse across the current sheet in the
-axis, as well as the resistive diffusion timescale,
which is the typical time required for magnetic flux to diffuse across the current sheet in the  -direction. The effective
Lundquist number for the problem is
-direction. The effective
Lundquist number for the problem is
 |
(9.26) |
Let
 ,
,
 ,
,
 ,
,
 ,
and
,
and
 . The dimensionless, normalized
versions of the linearized reduced-MHD equations, (9.22) and (9.23), become
. The dimensionless, normalized
versions of the linearized reduced-MHD equations, (9.22) and (9.23), become
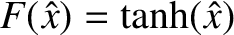 and
and
 . Our normalization scheme is designed such that, throughout the
bulk of the plasma,
. Our normalization scheme is designed such that, throughout the
bulk of the plasma,
 , and the only other quantities in the previous two equations whose magnitudes differ substantially
from unity are
, and the only other quantities in the previous two equations whose magnitudes differ substantially
from unity are
 and
and
 .
The term on the right-hand side of Equation (9.27) represents plasma resistivity, whereas the term on the left-hand side of Equation (9.28). represents plasma inertia.
The shear-Alfvén resonance condition,
.
The term on the right-hand side of Equation (9.27) represents plasma resistivity, whereas the term on the left-hand side of Equation (9.28). represents plasma inertia.
The shear-Alfvén resonance condition,
 , reduces to
, reduces to 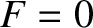 .
.