Next: Linearized Reduced-MHD Equations Up: Magnetic Reconnection Previous: Introduction Contents
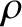 , and resistivity,
, and resistivity, 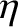 , are both assumed to be spatially uniform, for the sake of simplicity.
Compressibility is neglected (i.e.,
, are both assumed to be spatially uniform, for the sake of simplicity.
Compressibility is neglected (i.e.,
 is assumed to be zero) in order to decouple the fast and
slow magnetosonic waves from the problem. (See Section 8.4.) It turns out that the instabilities
that lead to magnetic reconnection in current sheets (so-called “tearing modes") are modified forms of the
shear-Alfvén wave (Hazeltine and Meiss 1985), and are not related to either of the magnetosonic waves.
Indeed, current sheets that exhibit magnetic reconnection resonate with the shear-Alfvén wave, whose dispersion relation is
is assumed to be zero) in order to decouple the fast and
slow magnetosonic waves from the problem. (See Section 8.4.) It turns out that the instabilities
that lead to magnetic reconnection in current sheets (so-called “tearing modes") are modified forms of the
shear-Alfvén wave (Hazeltine and Meiss 1985), and are not related to either of the magnetosonic waves.
Indeed, current sheets that exhibit magnetic reconnection resonate with the shear-Alfvén wave, whose dispersion relation is
 (see Section 8.4), where
(see Section 8.4), where 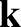 is the wavevector. A shear-Alfvén resonance occurs when
is the wavevector. A shear-Alfvén resonance occurs when 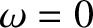 (i.e., when the wave frequency is reduced to zero), which implies that
(i.e., when the wave frequency is reduced to zero), which implies that
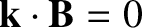 at the resonance.
at the resonance.
The three simplified MHD equations, (9.3)–(9.5), form a complete set when combined with Maxwell's equations:
Note that we are justified in neglecting the displacement current because we are dealing with waves whose phase velocities are small compared to the velocity of light in vacuum.
Consider a simplified scenario in which the Cartesian coordinate  is ignorable. In other words, there is
no variation in the
is ignorable. In other words, there is
no variation in the  -direction (i.e.,
-direction (i.e.,
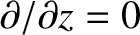 ), and no component of the magnetic field or the
plasma flow velocity in the
), and no component of the magnetic field or the
plasma flow velocity in the  -direction (i.e.,
-direction (i.e., 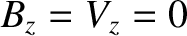 .) We can automatically satisfy Equations (9.3)
and (9.6) by writing
.) We can automatically satisfy Equations (9.3)
and (9.6) by writing
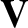 |
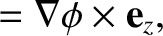 |
(9.9) |
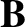 |
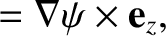 |
(9.10) |
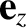 is a unit vector parallel to the
is a unit vector parallel to the  -axis. Note that
-axis. Note that
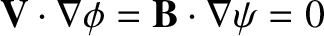 . Thus,
. Thus, 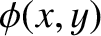 and
and 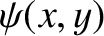 map out the flow stream-lines and
the magnetic field-lines, respectively, in the
map out the flow stream-lines and
the magnetic field-lines, respectively, in the  -
- plane.
plane. 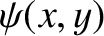 is usually referred to as magnetic flux,
because the net magnetic flux (per unit length in the
is usually referred to as magnetic flux,
because the net magnetic flux (per unit length in the  -direction) that passes through a surface (whose normal
lies in the
-direction) that passes through a surface (whose normal
lies in the  -
- plane) that links points (
plane) that links points ( ,
, 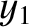 ) and (
) and (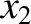 ,
, 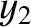 ) is
) is
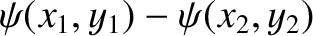 .
.
If we take the  -component of Equation (9.5), combined with Equations (9.7)–(9.10),
and the
-component of Equation (9.5), combined with Equations (9.7)–(9.10),
and the  -component of the curl of Equation (9.4), combined with Equations (9.8)–(9.10),
then we obtain the reduced-MHD equations (Strauss 1976):
-component of the curl of Equation (9.4), combined with Equations (9.8)–(9.10),
then we obtain the reduced-MHD equations (Strauss 1976):
![$[A,B]\equiv \nabla A\times \nabla B\cdot{\bf e}_z$](img3270.png) . Here, the current density is written
. Here, the current density is written
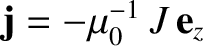 , and
, and
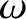
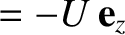 is the plasma vorticity.
Moreover,
is the plasma vorticity.
Moreover, 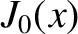 parametrizes the
parametrizes the  -directed inductive electric field that prevents the current in the current sheet from eventually
decaying to zero under the action of resistivity. The reduced-MHD equations are so-called because they do not contain the
full range of MHD physics (i.e., they do not contain the slow and fast magnetosonic waves).
-directed inductive electric field that prevents the current in the current sheet from eventually
decaying to zero under the action of resistivity. The reduced-MHD equations are so-called because they do not contain the
full range of MHD physics (i.e., they do not contain the slow and fast magnetosonic waves).