Next: Magnetic Pressure Up: Magnetohydrodynamic Fluids Previous: Magnetohydrodynamic Fluids Contents
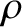 is the plasma mass density,
is the plasma mass density, 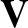 the center of mass velocity,
the center of mass velocity, 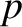 the pressure,
the pressure, 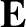 the
electric field-strength,
the
electric field-strength, 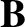 the magnetic field-strength, and
the magnetic field-strength, and
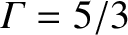 the
ratio of specific heats.
the
ratio of specific heats.
It is often remarked that Equations (8.1)–(8.4) are identical to the equations governing the motion of an inviscid, adiabatic, perfectly conducting, electrically neutral, liquid. Indeed, this observation is sometimes used as the sole justification for adopting the MHD equations. After all, a hot, tenuous, quasi-neutral plasma is highly conducting, and if the motion is sufficiently rapid then viscosity and heat conduction can both plausibly be neglected (which implies that the motion is adiabatic). However, as should be clear from the discussion in Section 4.12, this is a highly oversimplified and misleading argument. The problem, of course, is that a weakly coupled plasma is a far more complicated dynamical system than a conducting liquid.
According to the analysis of Section 4.12, the MHD equations are only valid when
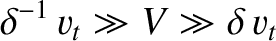 |
(8.5) |
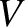 is the typical fluid velocity associated with the plasma
dynamics under investigation,
is the typical fluid velocity associated with the plasma
dynamics under investigation,
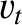 is the typical thermal velocity, and
is the typical thermal velocity, and 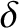 is the typical magnetization
parameter (i.e., the ratio of a particle gyroradius to
the scalelength of the motion). Clearly, the previous inequality is
most likely to be satisfied in a highly magnetized (i.e.,
is the typical magnetization
parameter (i.e., the ratio of a particle gyroradius to
the scalelength of the motion). Clearly, the previous inequality is
most likely to be satisfied in a highly magnetized (i.e.,
 ) plasma.
) plasma.
If the plasma dynamics becomes too rapid (i.e.,
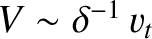 )
then resonances occur with the motions of individual particles
(e.g., the cyclotron resonances), which
invalidate the MHD equations. Furthermore, effects, such as electron
inertia and the Hall current, that are not (usually) taken into account in the
MHD equations, become important.
)
then resonances occur with the motions of individual particles
(e.g., the cyclotron resonances), which
invalidate the MHD equations. Furthermore, effects, such as electron
inertia and the Hall current, that are not (usually) taken into account in the
MHD equations, become important.
MHD is essentially a single-fluid plasma theory. A single-fluid
approach is justified because the perpendicular motion is dominated by
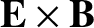 drifts, which are the same for both
plasma species. Furthermore,
the relative streaming velocity,
drifts, which are the same for both
plasma species. Furthermore,
the relative streaming velocity,
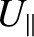 , of
both species parallel to the magnetic field is strongly constrained by the
fundamental MHD ordering (see Section 4.12)
, of
both species parallel to the magnetic field is strongly constrained by the
fundamental MHD ordering (see Section 4.12)
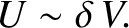 |
(8.6) |
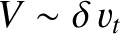 ) then the motions of the electron
and ion fluids become sufficiently different that a single-fluid
approach is no longer tenable. This occurs because the diamagnetic
velocities, which are quite different for different plasma species, become
comparable to the
) then the motions of the electron
and ion fluids become sufficiently different that a single-fluid
approach is no longer tenable. This occurs because the diamagnetic
velocities, which are quite different for different plasma species, become
comparable to the
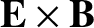 velocity. (See Section 4.15.)
Furthermore, effects such as plasma resistivity, viscosity, and thermal
conductivity, which are not (usually) taken into account in the MHD equations, become
important in this limit.
velocity. (See Section 4.15.)
Furthermore, effects such as plasma resistivity, viscosity, and thermal
conductivity, which are not (usually) taken into account in the MHD equations, become
important in this limit.
It follows, from the previous discussion, that the MHD equations describe relatively violent, large-scale motions of highly magnetized plasmas.
Strictly speaking, the MHD equations are only valid in collisional plasmas (i.e., plasmas in which the mean-free-path is much smaller than the typical variation scale-length). However, as is discussed in Section 4.16, the MHD equations also describe the perpendicular (but not the parallel) motions of collisionless plasmas fairly accurately.
Assuming that the MHD equations are valid, let us now investigate their properties.