Next: MacCullagh's formula Up: Rigid body rotation Previous: Euler angles
 is approximately
is approximately 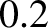 seconds of an arc
(which corresponds to a distance of about
seconds of an arc
(which corresponds to a distance of about
 on the Earth's surface).
The ratio of the terrestrial moments of inertia
is about
on the Earth's surface).
The ratio of the terrestrial moments of inertia
is about
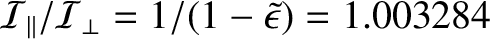 , as determined from luni-solar precession. (See Appendix F.) Hence, from Equation (8.40), the precession rate of the
angular velocity vector about the symmetry axis, as viewed in a geostationary reference frame, is
, as determined from luni-solar precession. (See Appendix F.) Hence, from Equation (8.40), the precession rate of the
angular velocity vector about the symmetry axis, as viewed in a geostationary reference frame, is
 |
(8.61) |
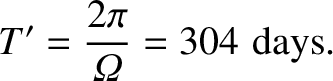 |
(8.62) |
 (sidereal) day.]
The observed period of precession is about 434 days (Yoder 1995). The disagreement
between theory and observation is attributed to the fact that the Earth
is not perfectly rigid (Bertotti et al. 2003). An improved treatment of the free precession of the Earth that takes into account its lack
of complete rigidity is given in Appendix E.
(sidereal) day.]
The observed period of precession is about 434 days (Yoder 1995). The disagreement
between theory and observation is attributed to the fact that the Earth
is not perfectly rigid (Bertotti et al. 2003). An improved treatment of the free precession of the Earth that takes into account its lack
of complete rigidity is given in Appendix E.
The Earth's symmetry axis subtends an angle
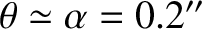 [see Equation (8.44)] with
its angular momentum vector, but it lies on the opposite side of this vector to the angular velocity vector.
This implies that, as viewed from space, the Earth's angular velocity vector is almost parallel to its
fixed angular momentum vector, whereas its symmetry axis subtends an angle of
[see Equation (8.44)] with
its angular momentum vector, but it lies on the opposite side of this vector to the angular velocity vector.
This implies that, as viewed from space, the Earth's angular velocity vector is almost parallel to its
fixed angular momentum vector, whereas its symmetry axis subtends an angle of 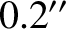 with both vectors and
precesses about them.
The (theoretical) precession rate of the Earth's symmetry
axis, as seen from space, is given by Equation (8.58):
with both vectors and
precesses about them.
The (theoretical) precession rate of the Earth's symmetry
axis, as seen from space, is given by Equation (8.58):
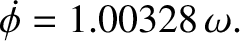 |
(8.63) |
 |
(8.64) |
The free precession of the Earth's symmetry axis in space, which is known as the Chandler wobble—because it was discovered by the American astronomer S.C. Chandler (1846–1913) in 1891—is superimposed on a much slower forced precession, with a period of about 26,000 years, caused by the small gravitational torque exerted on the Earth by the Sun and Moon, as a consequence of the Earth's slight oblateness. (See Section 8.10.)