MacCullagh's formula
According to Equations (3.59) and (3.64), if the Earth
is modeled as spheroid of uniform density  then its ellipticity
is given by
then its ellipticity
is given by
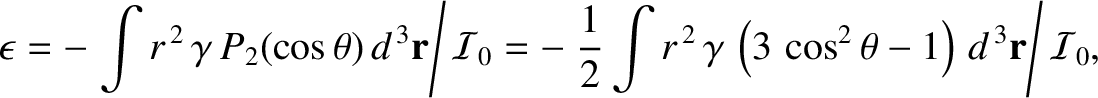 |
(8.65) |
where the integral is over the whole volume of the Earth, and
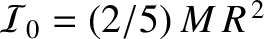 would be the Earth's moment of inertia were it
exactly spherical. The Earth's moment of inertia about its
axis of rotation is given by
would be the Earth's moment of inertia were it
exactly spherical. The Earth's moment of inertia about its
axis of rotation is given by
 |
(8.66) |
Here, use has been made of Equations (3.24)–(3.26). Likewise,
the Earth's moment of inertia about an axis perpendicular to its
axis of rotation (and passing through the Earth's center) is
because the average of
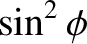 is
is  for an axisymmetric mass distribution. It follows from the preceding three equations that
for an axisymmetric mass distribution. It follows from the preceding three equations that
 |
(8.68) |
When Equation (8.68) is combined with Equation (3.65), we get
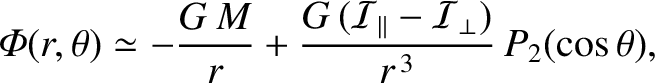 |
(8.69) |
which is the general expression for the gravitational potential generated outside
an axially symmetric mass distribution. The first term on the right-hand
side is the monopole gravitational potential that would be generated
if all of the mass in the distribution were concentrated at its center of mass,
whereas the second term is the quadrupole potential generated by any deviation from spherical symmetry in the distribution.
Equation (8.69) actually holds for any axially symmetric mass distribution, not just a spheroidal mass distribution of
uniform density (this is discussed in the following).
More generally, consider an asymmetric mass distribution consisting of 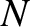 mass elements. Suppose that the
mass elements. Suppose that the
 th element has mass
th element has mass 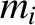 and
position vector
and
position vector 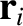 , where
, where  runs from
runs from  to
to 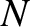 . Let us define a Cartesian coordinate system
. Let us define a Cartesian coordinate system  ,
,  ,
,  such that the
origin coincides with the center of mass of the distribution. It follows that
such that the
origin coincides with the center of mass of the distribution. It follows that
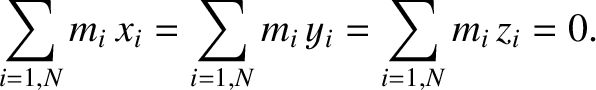 |
(8.70) |
Suppose that the  -,
-,  -, and
-, and  -axes coincide with the mass distribution's principal axes of rotation (for rotation
about an axis that passes through the origin). It follows from
Section 8.5 that
-axes coincide with the mass distribution's principal axes of rotation (for rotation
about an axis that passes through the origin). It follows from
Section 8.5 that
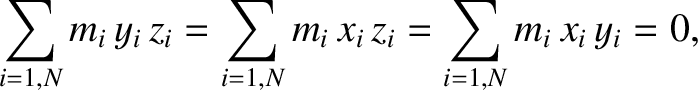 |
(8.71) |
and that the distribution's principal moments of inertia about the  -,
-,  -, and
-, and  -axes take the form
respectively.
-axes take the form
respectively.
Figure 8.3:
A general mass distribution.
|
|
Consider the gravitational potential,
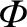 , generated by the mass distribution at some external point
, generated by the mass distribution at some external point 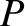 whose position
vector is
whose position
vector is
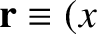 ,
,  ,
,  . According to Section 3.2,
. According to Section 3.2,
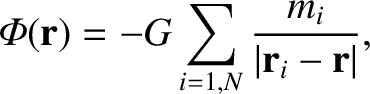 |
(8.75) |
which can also be written
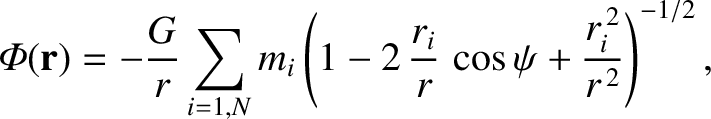 |
(8.76) |
where 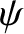 is the angle subtended between the vectors
is the angle subtended between the vectors  and
and 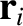 . See Figure 8.3. Suppose that
the distance
. See Figure 8.3. Suppose that
the distance
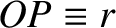 is much larger than the characteristic radius of the mass distribution, which implies that
is much larger than the characteristic radius of the mass distribution, which implies that
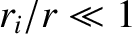 for all
for all  . Expanding up to second order in
. Expanding up to second order in 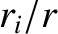 , we obtain
, we obtain
![$\displaystyle {\mit\Phi}({\bf r})\simeq -\frac{G}{r}\sum_{i=1,N}m_i\left[1+\fra...
...si+ \frac{1}{2}\,\frac{r_i^{\,2}}{r^{\,2}}
\left(3\,\cos^2\psi-1\right)\right].$](img1683.png) |
(8.77) |
However,
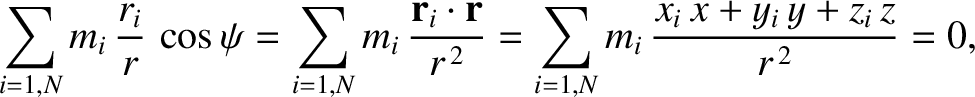 |
(8.78) |
where use has been made of Equations (8.70).
Hence, we are left with
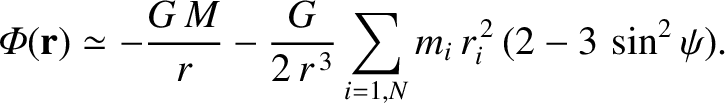 |
(8.79) |
Here,
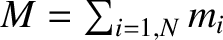 is the total mass of the distribution.
Now,
where use has been made of Equations (8.72)–(8.74). Furthermore,
is the total mass of the distribution.
Now,
where use has been made of Equations (8.72)–(8.74). Furthermore,
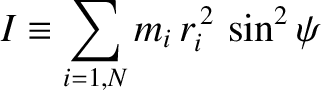 |
(8.81) |
is the distribution's moment of inertia about the axis 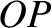 . Thus, we deduce that
. Thus, we deduce that
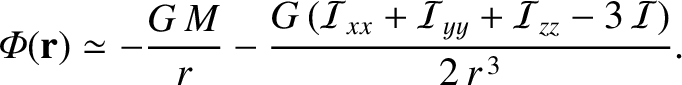 |
(8.82) |
This famous result is known as MacCullagh's formula, after its discoverer, the Irish mathematician James MacCullagh (1809–1847).
Actually,
Hence, MacCullagh's formula can also be written in the alternative form
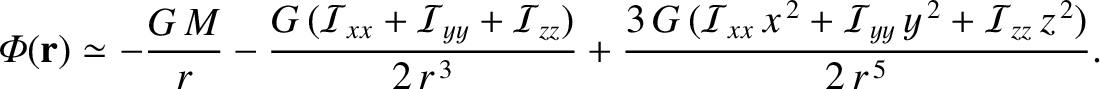 |
(8.84) |
Finally, for an axisymmetric distribution, such that
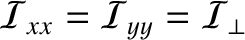 and
and
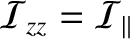 , MacCullagh's formula reduces to
, MacCullagh's formula reduces to
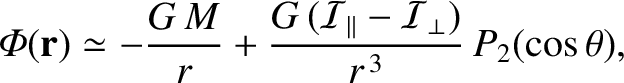 |
(8.85) |
where
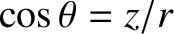 .
Of course, this expression is the same as Equation (8.69), which justifies our earlier assertion that this equation is
is valid for a general axisymmetric mass distribution. Incidentally, a comparison of the preceding expression with
Equation (3.66) reveals that
.
Of course, this expression is the same as Equation (8.69), which justifies our earlier assertion that this equation is
is valid for a general axisymmetric mass distribution. Incidentally, a comparison of the preceding expression with
Equation (3.66) reveals that
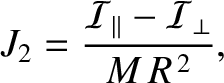 |
(8.86) |
where  is the mean radius of the distribution, and the dimensionless parameter
is the mean radius of the distribution, and the dimensionless parameter 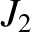 characterizes the
quadrupole gravitational field external to the distribution.
characterizes the
quadrupole gravitational field external to the distribution.
 then its ellipticity
is given by
then its ellipticity
is given by
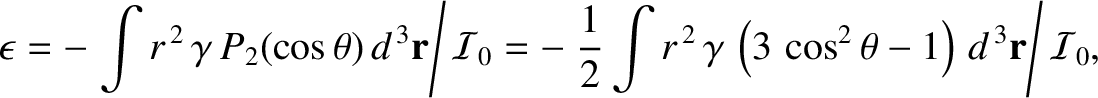
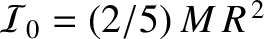 would be the Earth's moment of inertia were it
exactly spherical. The Earth's moment of inertia about its
axis of rotation is given by
would be the Earth's moment of inertia were it
exactly spherical. The Earth's moment of inertia about its
axis of rotation is given by

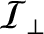
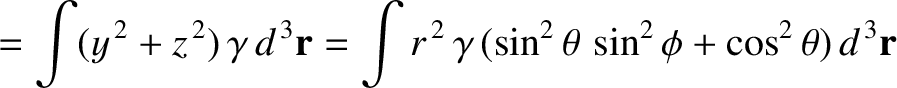
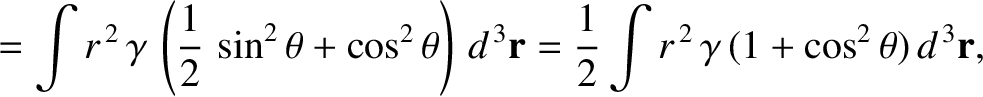
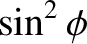 is
is  for an axisymmetric mass distribution. It follows from the preceding three equations that
When Equation (8.68) is combined with Equation (3.65), we get
which is the general expression for the gravitational potential generated outside
an axially symmetric mass distribution. The first term on the right-hand
side is the monopole gravitational potential that would be generated
if all of the mass in the distribution were concentrated at its center of mass,
whereas the second term is the quadrupole potential generated by any deviation from spherical symmetry in the distribution.
Equation (8.69) actually holds for any axially symmetric mass distribution, not just a spheroidal mass distribution of
uniform density (this is discussed in the following).
for an axisymmetric mass distribution. It follows from the preceding three equations that
When Equation (8.68) is combined with Equation (3.65), we get
which is the general expression for the gravitational potential generated outside
an axially symmetric mass distribution. The first term on the right-hand
side is the monopole gravitational potential that would be generated
if all of the mass in the distribution were concentrated at its center of mass,
whereas the second term is the quadrupole potential generated by any deviation from spherical symmetry in the distribution.
Equation (8.69) actually holds for any axially symmetric mass distribution, not just a spheroidal mass distribution of
uniform density (this is discussed in the following).
 mass elements. Suppose that the
mass elements. Suppose that the
 th element has mass
th element has mass 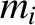 and
position vector
and
position vector 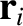 , where
, where  runs from
runs from  to
to 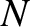 . Let us define a Cartesian coordinate system
. Let us define a Cartesian coordinate system  ,
,  ,
,  such that the
origin coincides with the center of mass of the distribution. It follows that
such that the
origin coincides with the center of mass of the distribution. It follows that
 -,
-,  -, and
-, and  -axes coincide with the mass distribution's principal axes of rotation (for rotation
about an axis that passes through the origin). It follows from
Section 8.5 that
-axes coincide with the mass distribution's principal axes of rotation (for rotation
about an axis that passes through the origin). It follows from
Section 8.5 that
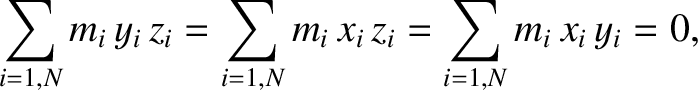
 -,
-,  -, and
-, and  -axes take the form
respectively.
-axes take the form
respectively.
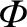 , generated by the mass distribution at some external point
, generated by the mass distribution at some external point 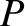 whose position
vector is
whose position
vector is
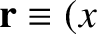 ,
,  ,
,  . According to Section 3.2,
. According to Section 3.2,
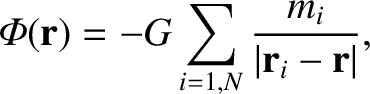
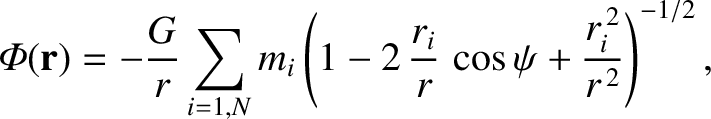
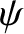 is the angle subtended between the vectors
is the angle subtended between the vectors  and
and 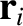 . See Figure 8.3. Suppose that
the distance
. See Figure 8.3. Suppose that
the distance
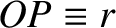 is much larger than the characteristic radius of the mass distribution, which implies that
is much larger than the characteristic radius of the mass distribution, which implies that
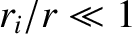 for all
for all  . Expanding up to second order in
. Expanding up to second order in 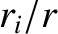 , we obtain
, we obtain
![$\displaystyle {\mit\Phi}({\bf r})\simeq -\frac{G}{r}\sum_{i=1,N}m_i\left[1+\fra...
...si+ \frac{1}{2}\,\frac{r_i^{\,2}}{r^{\,2}}
\left(3\,\cos^2\psi-1\right)\right].$](img1683.png)
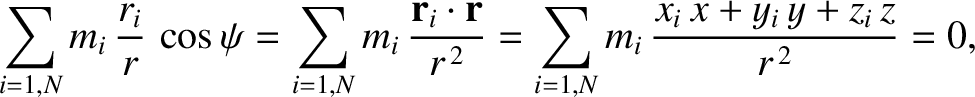
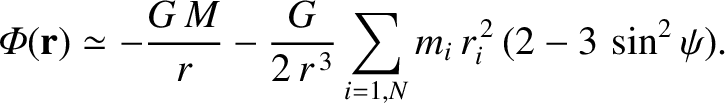
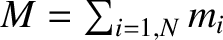 is the total mass of the distribution.
Now,
is the total mass of the distribution.
Now,
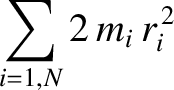
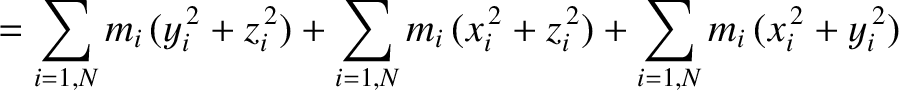
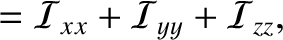
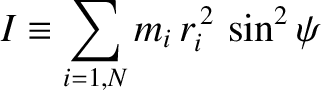
 . Thus, we deduce that
. Thus, we deduce that
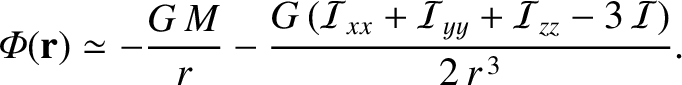
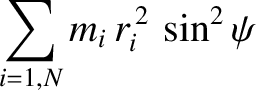

 and
and
 , MacCullagh's formula reduces to
, MacCullagh's formula reduces to
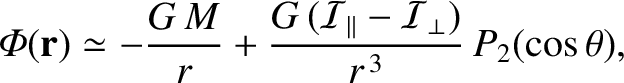
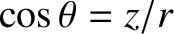 .
Of course, this expression is the same as Equation (8.69), which justifies our earlier assertion that this equation is
is valid for a general axisymmetric mass distribution. Incidentally, a comparison of the preceding expression with
Equation (3.66) reveals that
where
.
Of course, this expression is the same as Equation (8.69), which justifies our earlier assertion that this equation is
is valid for a general axisymmetric mass distribution. Incidentally, a comparison of the preceding expression with
Equation (3.66) reveals that
where  is the mean radius of the distribution, and the dimensionless parameter
is the mean radius of the distribution, and the dimensionless parameter 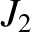 characterizes the
quadrupole gravitational field external to the distribution.
characterizes the
quadrupole gravitational field external to the distribution.