Next: Free precession of Earth Up: Rigid body rotation Previous: Euler's equations
The fixed frame and the body frame share the same origin. Hence, we can transform from one to the other by means of an appropriate rotation of our coordinate axes. In general, if we restrict ourselves to rotations about one of the Cartesian axes, three successive rotations are required to transform the fixed frame into the body frame. There are, in fact, many different ways to combined three successive rotations in order to achieve this goal. In the following, we shall describe the most widely used method, which is due to Euler.
We start in the fixed frame, which has coordinates  ,
,  ,
,  , and
unit vectors
, and
unit vectors 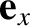 ,
,  ,
, 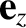 . Our first rotation
is counterclockwise (if we look down the axis) through an angle
. Our first rotation
is counterclockwise (if we look down the axis) through an angle  about the
about the  -axis. The new frame has coordinates
-axis. The new frame has coordinates 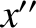 ,
,  ,
, 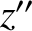 , and
unit vectors
, and
unit vectors
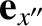 ,
,
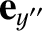 ,
,
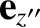 . According
to Section A.6, the transformation of coordinates can be represented as
follows:
. According
to Section A.6, the transformation of coordinates can be represented as
follows:
 has the magnitude
has the magnitude
 ,
and is directed along
,
and is directed along 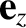 (i.e., along the axis of rotation).
Hence, we can write
Clearly,
(i.e., along the axis of rotation).
Hence, we can write
Clearly,
 is the precession rate about the
is the precession rate about the  -axis,
as seen in the fixed frame.
-axis,
as seen in the fixed frame.
The second rotation is counterclockwise (if we look down the axis) through
an angle  about the
about the 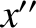 -axis. The new frame has coordinates
-axis. The new frame has coordinates
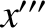 ,
, 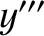 ,
, 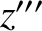 , and unit vectors
, and unit vectors
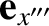 ,
,
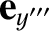 ,
,
 . By analogy with Equation (8.45), the transformation
of coordinates can be represented as follows:
. By analogy with Equation (8.45), the transformation
of coordinates can be represented as follows:
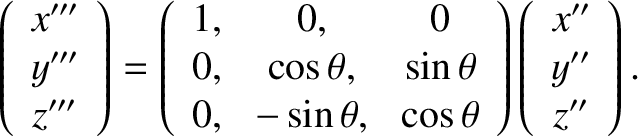 |
(8.47) |
 has the magnitude
has the magnitude
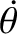 ,
and is directed along
,
and is directed along
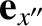 (i.e., along the axis of rotation).
Hence, we can write
(i.e., along the axis of rotation).
Hence, we can write
The third rotation is counterclockwise (if we look down the axis) through
an angle 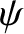 about the
about the 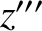 -axis. The new frame is the body frame, which has coordinates
-axis. The new frame is the body frame, which has coordinates
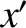 ,
, 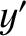 ,
, 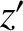 , and unit vectors
, and unit vectors
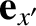 ,
,
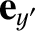 ,
,
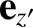 . The transformation of coordinates can be represented as
follows:
. The transformation of coordinates can be represented as
follows:
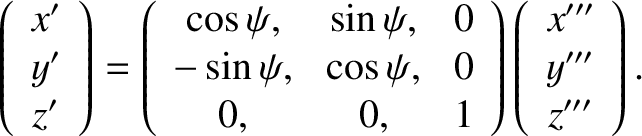 |
(8.49) |
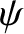 has the magnitude
has the magnitude
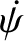 ,
and is directed along
,
and is directed along
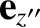 (i.e., along the axis of rotation).
Note that
(i.e., along the axis of rotation).
Note that
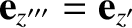 , because the third rotation is about
, because the third rotation is about
 .
Hence, we can write
Clearly,
.
Hence, we can write
Clearly,
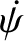 is minus the precession rate about the
is minus the precession rate about the 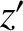 -axis, as seen in the body frame.
-axis, as seen in the body frame.
The full transformation between the fixed frame and the body frame is rather complicated. However, the following results can easily be verified:
It follows from Equation (8.51) that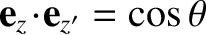 . In other words,
. In other words,  is the angle of inclination between the
is the angle of inclination between the
 - and
- and 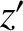 -axes.
Finally, because the total angular velocity can be written
Equations (8.46), (8.48), and (8.50)–(8.52)
yield
-axes.
Finally, because the total angular velocity can be written
Equations (8.46), (8.48), and (8.50)–(8.52)
yield
The angles  ,
,  , and
, and 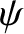 are termed Euler angles. Each has a clear physical interpretation:
are termed Euler angles. Each has a clear physical interpretation:  is the angle of precession
about the
is the angle of precession
about the  -axis in the fixed frame,
-axis in the fixed frame, 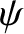 is minus the angle of precession about the
is minus the angle of precession about the
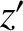 -axis in the body frame, and
-axis in the body frame, and  is the angle of inclination
between the
is the angle of inclination
between the  - and
- and 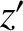 - axes. Moreover, we can
express the components of the angular velocity vector
- axes. Moreover, we can
express the components of the angular velocity vector
 in the body frame entirely in terms of the Eulerian angles, and their time derivatives. [See Equations (8.54)–(8.56).]
in the body frame entirely in terms of the Eulerian angles, and their time derivatives. [See Equations (8.54)–(8.56).]
Consider a freely rotating body that is rotationally symmetric about one axis (the 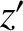 -axis). In the absence of an external torque, the
angular momentum vector
-axis). In the absence of an external torque, the
angular momentum vector 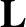 is a constant of the motion. [See Equation (8.3).] Let
is a constant of the motion. [See Equation (8.3).] Let 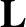 point along the
point along the  -axis. In the
previous section, we saw that the angular momentum vector subtends a
constant angle
-axis. In the
previous section, we saw that the angular momentum vector subtends a
constant angle  with the axis of symmetry; that is, with the
with the axis of symmetry; that is, with the 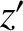 -axis. Hence, the time derivative
of the Eulerian angle
-axis. Hence, the time derivative
of the Eulerian angle  is zero. We also saw that the angular momentum
vector, the axis of symmetry, and the angular velocity vector are coplanar.
Consider an instant in time at which all of these vectors lie in the
is zero. We also saw that the angular momentum
vector, the axis of symmetry, and the angular velocity vector are coplanar.
Consider an instant in time at which all of these vectors lie in the 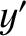 -
-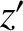 plane. This implies that
plane. This implies that
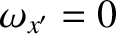 . According to the
previous section, the angular velocity vector subtends a constant
angle
. According to the
previous section, the angular velocity vector subtends a constant
angle  with the symmetry axis. It follows that
with the symmetry axis. It follows that
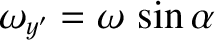 and
and
 . Equation (8.54) gives
. Equation (8.54) gives
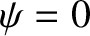 . Hence, Equation (8.55) yields
. Hence, Equation (8.55) yields
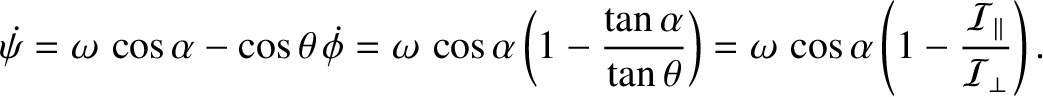 |
(8.59) |
 |
(8.60) |
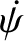 is minus the precession rate (of the angular
momentum and angular velocity vectors) in the body frame. On the other hand,
is minus the precession rate (of the angular
momentum and angular velocity vectors) in the body frame. On the other hand,
 is the precession rate (of the angular velocity vector
and the symmetry axis) in the
fixed frame. Note that
is the precession rate (of the angular velocity vector
and the symmetry axis) in the
fixed frame. Note that
 and
and
 are
quite dissimilar. For instance,
are
quite dissimilar. For instance,
 is negative for elongated
bodies (
is negative for elongated
bodies (
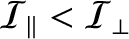 ) whereas
) whereas
 is positive definite. It follows that the precession is always in the
same sense as
is positive definite. It follows that the precession is always in the
same sense as 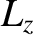 in the fixed frame, whereas the
precession in the body frame is in the opposite sense to
in the fixed frame, whereas the
precession in the body frame is in the opposite sense to  for elongated bodies. We
found, in the previous section, that for a flattened body the angular
momentum vector lies between the angular velocity vector and the symmetry
axis. This means that, in the fixed frame, the angular velocity vector
and the symmetry axis lie on opposite sides of the fixed angular
momentum vector, about which they precess. See Figure 8.2. On the other hand, for an elongated body
we found that the angular velocity vector lies between the angular momentum
vector and the symmetry axis. This means that, in the fixed frame, the
angular velocity vector and the symmetry axis lie on the same side of
the fixed angular momentum vector, about which they precess. See Figure 8.2. (Recall that the angular
momentum vector, the angular velocity vector, and the symmetry
axis are coplanar.)
for elongated bodies. We
found, in the previous section, that for a flattened body the angular
momentum vector lies between the angular velocity vector and the symmetry
axis. This means that, in the fixed frame, the angular velocity vector
and the symmetry axis lie on opposite sides of the fixed angular
momentum vector, about which they precess. See Figure 8.2. On the other hand, for an elongated body
we found that the angular velocity vector lies between the angular momentum
vector and the symmetry axis. This means that, in the fixed frame, the
angular velocity vector and the symmetry axis lie on the same side of
the fixed angular momentum vector, about which they precess. See Figure 8.2. (Recall that the angular
momentum vector, the angular velocity vector, and the symmetry
axis are coplanar.)
![\includegraphics[height=2.75in]{Chapter07/fig7_02.eps}](img1649.png)
|