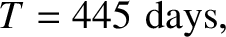Free precession of Earth
This appendix extends the treatment of the free precession of the Earth's axis of rotation, presented in Section 8.8, to take
into account the fact that the Earth is not a completely rigid body.
The Earth is modeled as a nearly spherical body, of uniform mass density  , whose boundary lies at
, whose boundary lies at
 |
(E.1) |
where
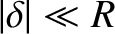 .
Here,
.
Here,  ,
,  ,
,  are standard spherical coordinates in the terrestrial body frame. (See Section 8.6.) Moreover,
are standard spherical coordinates in the terrestrial body frame. (See Section 8.6.) Moreover,  is the Earth's mean radius.
The terrestrial mass density field is well approximated as
is the Earth's mean radius.
The terrestrial mass density field is well approximated as
 |
(E.2) |
where
 is a Dirac delta function (Riley 1974b), and
is a Dirac delta function (Riley 1974b), and
![\begin{displaymath}\rho_0(r)=\left\{
\begin{array}{lll}
\gamma&\mbox{\hspace{0.5cm}}&r\leq R\\ [0.5ex]
0&&r>R
\end{array}\right. .\end{displaymath}](img4444.png) |
(E.3) |
Finally,
where the first term on the right-hand side describes the Earth's rotational flattening (see Section 6.5), whereas the second is the additional displacement of the
Earth's surface caused by its lack of complete rigidity. The dimensionless parameter  , which measures the degree of rotational
flattening, is termed the ellipticity. (See Section 3.6.) Here, the
, which measures the degree of rotational
flattening, is termed the ellipticity. (See Section 3.6.) Here, the
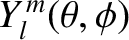 are spherical harmonics. (See Section A.12.)
are spherical harmonics. (See Section A.12.)
Let
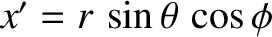 ,
,
 ,
,
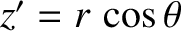 be Cartesian coordinates in the Earth's body frame. In particular, let the
be Cartesian coordinates in the Earth's body frame. In particular, let the 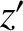 -axis
correspond to the symmetry axis passing through the Earth's geographic poles. Suppose that the Earth's angular velocity vector,
-axis
correspond to the symmetry axis passing through the Earth's geographic poles. Suppose that the Earth's angular velocity vector,
 , is slightly inclined to its symmetry axis, such that
, is slightly inclined to its symmetry axis, such that
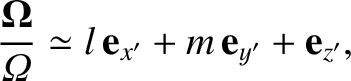 |
(E.5) |
where 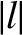 ,
,  . In the following, we shall neglect terms that are second order in the small quantities
. In the following, we shall neglect terms that are second order in the small quantities 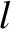 and
and  .
.
The Earth rotational flattening is a response to the conventional centrifugal potential
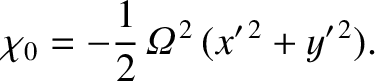 |
(E.6) |
(See Section 6.5.) However, the previous potential is calculated on the assumption that the Earth's axis of rotation coincides exactly with
its symmetry axis. In fact, because the two axes are slightly inclined to one another, the true centrifugal potential is
Thus, there is a residual potential,
that is not compensated by the Earth's rotational flattening, and to which the Earth responds elastically. Note that this potential is a solid harmonic
of degree 2. (See Section C.2.)
According to the analysis of Section C.4, the elastic response of the Earth to the residual potential is such that
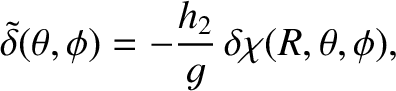 |
(E.9) |
where
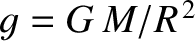 is the Earth's surface gravity, and
is the Earth's surface gravity, and
 its mass. Here, the dimensionless parameter
its mass. Here, the dimensionless parameter 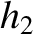 is a measure of terrestrial rigidity. In fact,
is a measure of terrestrial rigidity. In fact, 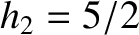 in the limit of zero rigidity, and
in the limit of zero rigidity, and 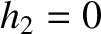 in the opposite limit of complete rigidity. [See Equation (C.50).]
It follows that the net radial displacement of the Earth's surface, in response to the overall centrifugal potential, can be written
in the opposite limit of complete rigidity. [See Equation (C.50).]
It follows that the net radial displacement of the Earth's surface, in response to the overall centrifugal potential, can be written
![$\displaystyle \delta(\theta,\phi) =- \frac{2}{3}\sqrt{\frac{4\pi}{5}}\,\epsilon...
...h_2\,\zeta\,R\left[(l-{\rm i}\,m)\,Y_2^{\,1}-(l+{\rm i}\,m)\,Y_2^{\,-1}\right],$](img4465.png) |
(E.10) |
where
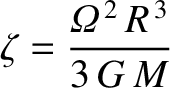 |
(E.11) |
is a dimensionless parameter that measures the strength of the centrifugal potential. (See Section 6.5.)
Now, it is easily shown that
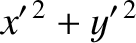 |
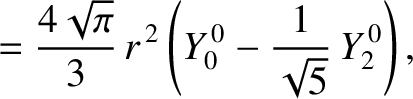 |
(E.12) |
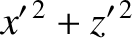 |
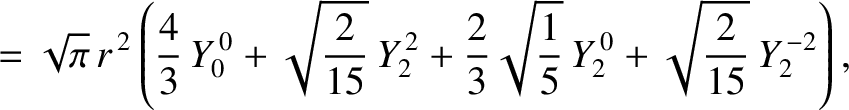 |
(E.13) |
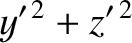 |
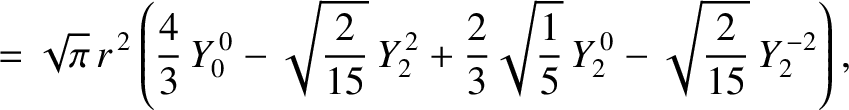 |
(E.14) |
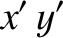 |
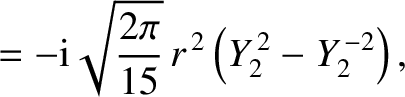 |
(E.15) |
 |
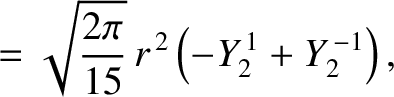 |
(E.16) |
 |
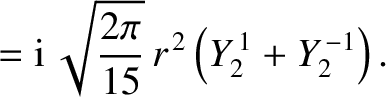 |
(E.17) |
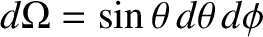 is an element of solid angle, and use has been made of Equations (E.2), (E.3), and (E.12).
Similarly, the other elements of the moment of inertia tensor (see Section 8.3) are written
is an element of solid angle, and use has been made of Equations (E.2), (E.3), and (E.12).
Similarly, the other elements of the moment of inertia tensor (see Section 8.3) are written
 |
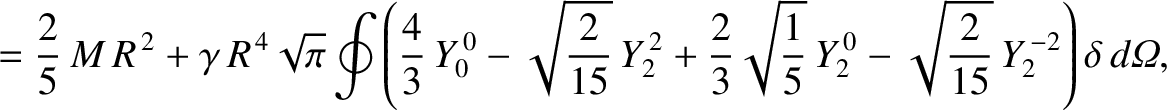 |
(E.19) |
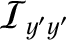 |
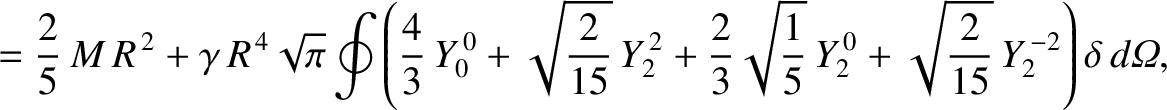 |
(E.20) |
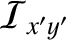 |
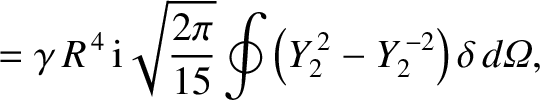 |
(E.21) |
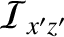 |
 |
(E.22) |
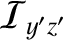 |
 |
(E.23) |
 |
(E.24) |
Hence, combining Equations (E.10) with Equations (E.18)–(E.23), we deduce that
where
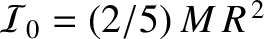 . It can be seen that the elastic yielding of the Earth introduces small off-diagonal elements into its moment of inertia tensor,
but does not affect the diagonal elements.
. It can be seen that the elastic yielding of the Earth introduces small off-diagonal elements into its moment of inertia tensor,
but does not affect the diagonal elements.
The components of the Earth's angular momentum vector, 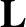 , take the form (see Section 8.3),
, take the form (see Section 8.3),
According to Equation (8.25), in the absence of an external torque, the Earth's rotational equation of motion is written
where 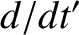 denotes a time derivative in the body frame. Assuming that the direction cosines
denotes a time derivative in the body frame. Assuming that the direction cosines 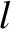 and
and  are the only quantities that evolve in time, the
are the only quantities that evolve in time, the
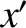 - and
- and 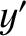 -components of the previous equation yield
respectively, where
-components of the previous equation yield
respectively, where
![$\displaystyle \omega =\left[\frac{{\cal I}_\parallel-(1+3\,h_2\,\zeta/2)\,{\cal I}_\perp}{(1+3\,h_2\,\zeta/2)\,{\cal I}_\perp}\right]{\mit\Omega}.$](img4504.png) |
(E.37) |
It follows that, in the body frame,
where  is the arbitrary angle of inclination between the Earth's axis of rotation and its symmetry axis. Of course, for consistency with our
previous analysis, this angle must be small. The previous two equations indicate that, in the body frame, the Earth's axis of rotation precesses about
its symmetry axis at the angular frequency
is the arbitrary angle of inclination between the Earth's axis of rotation and its symmetry axis. Of course, for consistency with our
previous analysis, this angle must be small. The previous two equations indicate that, in the body frame, the Earth's axis of rotation precesses about
its symmetry axis at the angular frequency  . The period of this precession in sidereal days is
. The period of this precession in sidereal days is
 |
(E.40) |
where
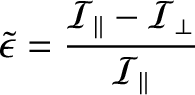 |
(E.41) |
is the Earth's dynamical ellipticity. (See Section 8.10 and Appendix F.) Note that, were the Earth completely rigid (i.e., 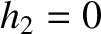 ), the
precession period would be
), the
precession period would be
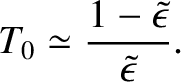 |
(E.42) |
Approximating the Earth as a uniform elastic body of uniform rigidity  , we find that
, we find that
 [i.e., the Earth's
dynamical ellipticity is equal to the actual ellipticity due to its slightly flattened shape; see Equations (E.25)–(E.27)] and
[i.e., the Earth's
dynamical ellipticity is equal to the actual ellipticity due to its slightly flattened shape; see Equations (E.25)–(E.27)] and
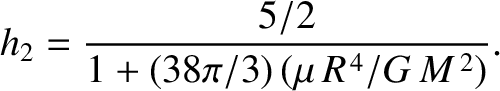 |
(E.43) |
[See Equation (C.50).] Using
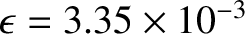 ,
,
 ,
,
 ,
,
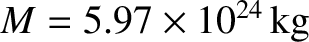 , and
, and
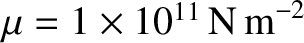 (see Section 6.5), we
deduce that
Hence, our estimate for the free precession period of the Earth's axis of rotation (in its body frame) becomes
(see Section 6.5), we
deduce that
Hence, our estimate for the free precession period of the Earth's axis of rotation (in its body frame) becomes
 |
(E.46) |
If the Earth were modeled as completely rigid then the corresponding precession period would be
 |
(E.47) |
Now, the observed precession period is  days (Yoder 1995). Thus, our estimate for the precession period that takes the Earth's lack of
complete rigidity into account is far closer to the correct answer than our estimate that treats the Earth as a completely rigid body.
days (Yoder 1995). Thus, our estimate for the precession period that takes the Earth's lack of
complete rigidity into account is far closer to the correct answer than our estimate that treats the Earth as a completely rigid body.
We can improve our estimate for the Earth's free precession period by taking into account the fact that the Earth is not actually a uniform
body. This is possible because Equation (E.40) turns out to be completely general (i.e., although it was derived on the assumption that the
Earth is a uniform body, it remains valid for a non-uniform Earth) (Love 1909). The Earth's actual dynamical ellipticity, which is deduced from the measured
rate of luni-solar precession, turns out to be
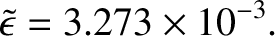 |
(E.48) |
(See Appendix F.) Furthermore, the value of the Love number 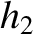 , which is deduced from the measured yielding of the Earth to the Moon's
tidal gravitational field, is
, which is deduced from the measured yielding of the Earth to the Moon's
tidal gravitational field, is
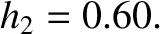 |
(E.49) |
(Love 1909.)
Hence, our improved estimate for the Earth's free precession period becomes
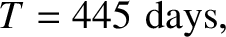 |
(E.50) |
which lies within 3 percent of the correct answer. The corresponding precession period for a completely rigid Earth is
 |
(E.51) |
(See Section 8.8.) The remaining difference between our improved estimate for the Earth's free precession period and the
observed precession period can be explained by taking into account the effect of the Earth's fluid core, as well as the fact that much of its surface is covered with fluid oceans (Smith and Dahlen 1981).
 , whose boundary lies at
, whose boundary lies at

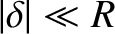 .
Here,
.
Here,  ,
,  ,
,  are standard spherical coordinates in the terrestrial body frame. (See Section 8.6.) Moreover,
are standard spherical coordinates in the terrestrial body frame. (See Section 8.6.) Moreover,  is the Earth's mean radius.
The terrestrial mass density field is well approximated as
where
is the Earth's mean radius.
The terrestrial mass density field is well approximated as
where
 is a Dirac delta function (Riley 1974b), and
Finally,
is a Dirac delta function (Riley 1974b), and
Finally,
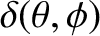
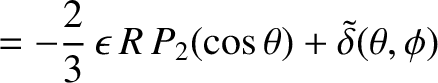
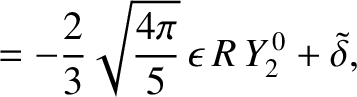
 , which measures the degree of rotational
flattening, is termed the ellipticity. (See Section 3.6.) Here, the
, which measures the degree of rotational
flattening, is termed the ellipticity. (See Section 3.6.) Here, the
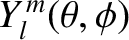 are spherical harmonics. (See Section A.12.)
are spherical harmonics. (See Section A.12.)
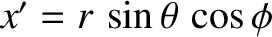 ,
,
 ,
,
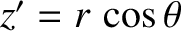 be Cartesian coordinates in the Earth's body frame. In particular, let the
be Cartesian coordinates in the Earth's body frame. In particular, let the 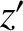 -axis
correspond to the symmetry axis passing through the Earth's geographic poles. Suppose that the Earth's angular velocity vector,
-axis
correspond to the symmetry axis passing through the Earth's geographic poles. Suppose that the Earth's angular velocity vector,
 , is slightly inclined to its symmetry axis, such that
, is slightly inclined to its symmetry axis, such that
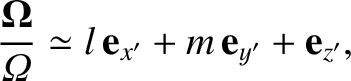
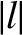 ,
,  . In the following, we shall neglect terms that are second order in the small quantities
. In the following, we shall neglect terms that are second order in the small quantities 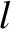 and
and  .
.
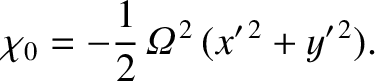
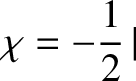

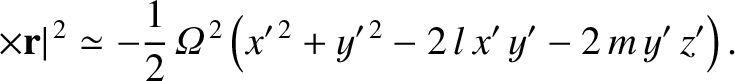

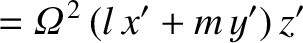
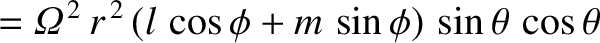
![$\displaystyle = \sqrt{\frac{2\pi}{15}}\,{\mit\Omega}^{\,2}\,r^{\,2}\left[(l+{\rm i}\,m)\,Y_2^{\,-1}-(l-{\rm i}\,m)\,Y_2^{\,1}\right],$](img4460.png)
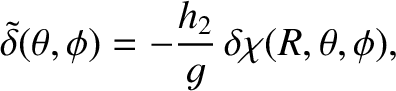
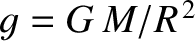 is the Earth's surface gravity, and
is the Earth's surface gravity, and
 its mass. Here, the dimensionless parameter
its mass. Here, the dimensionless parameter 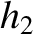 is a measure of terrestrial rigidity. In fact,
is a measure of terrestrial rigidity. In fact, 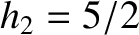 in the limit of zero rigidity, and
in the limit of zero rigidity, and 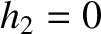 in the opposite limit of complete rigidity. [See Equation (C.50).]
It follows that the net radial displacement of the Earth's surface, in response to the overall centrifugal potential, can be written
where
in the opposite limit of complete rigidity. [See Equation (C.50).]
It follows that the net radial displacement of the Earth's surface, in response to the overall centrifugal potential, can be written
where
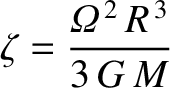
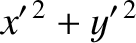
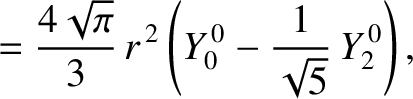
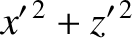
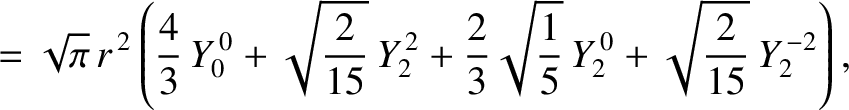
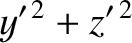
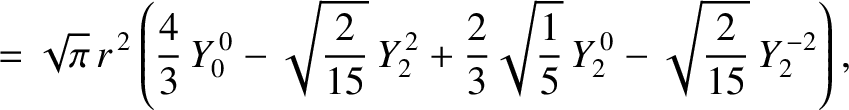
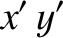
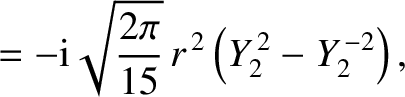
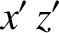
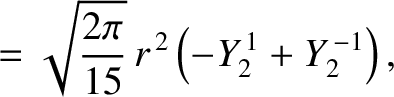
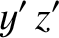
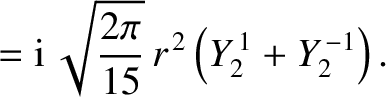
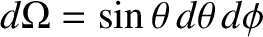 is an element of solid angle, and use has been made of Equations (E.2), (E.3), and (E.12).
Similarly, the other elements of the moment of inertia tensor (see Section 8.3) are written
is an element of solid angle, and use has been made of Equations (E.2), (E.3), and (E.12).
Similarly, the other elements of the moment of inertia tensor (see Section 8.3) are written

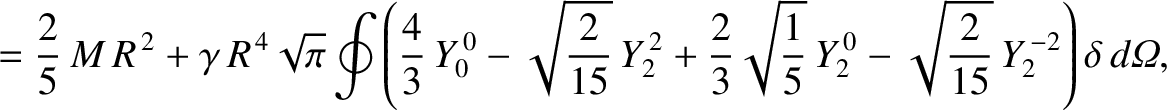
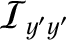
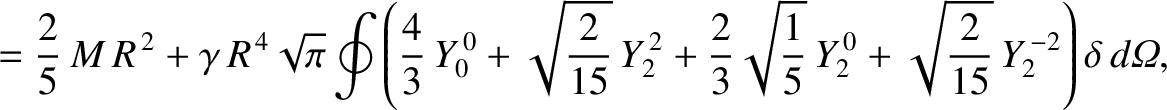
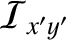
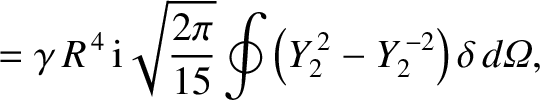
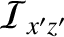



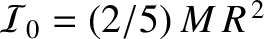 . It can be seen that the elastic yielding of the Earth introduces small off-diagonal elements into its moment of inertia tensor,
but does not affect the diagonal elements.
. It can be seen that the elastic yielding of the Earth introduces small off-diagonal elements into its moment of inertia tensor,
but does not affect the diagonal elements.
 , take the form (see Section 8.3),
, take the form (see Section 8.3),
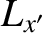
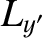
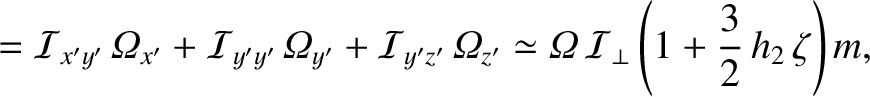
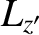

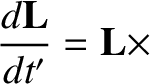

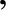
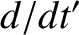 denotes a time derivative in the body frame. Assuming that the direction cosines
denotes a time derivative in the body frame. Assuming that the direction cosines 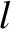 and
and  are the only quantities that evolve in time, the
are the only quantities that evolve in time, the
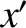 - and
- and 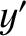 -components of the previous equation yield
-components of the previous equation yield
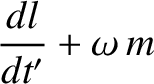
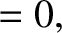

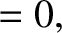
![$\displaystyle \omega =\left[\frac{{\cal I}_\parallel-(1+3\,h_2\,\zeta/2)\,{\cal I}_\perp}{(1+3\,h_2\,\zeta/2)\,{\cal I}_\perp}\right]{\mit\Omega}.$](img4504.png)

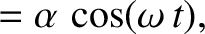

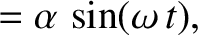
 is the arbitrary angle of inclination between the Earth's axis of rotation and its symmetry axis. Of course, for consistency with our
previous analysis, this angle must be small. The previous two equations indicate that, in the body frame, the Earth's axis of rotation precesses about
its symmetry axis at the angular frequency
is the arbitrary angle of inclination between the Earth's axis of rotation and its symmetry axis. Of course, for consistency with our
previous analysis, this angle must be small. The previous two equations indicate that, in the body frame, the Earth's axis of rotation precesses about
its symmetry axis at the angular frequency  . The period of this precession in sidereal days is
where
. The period of this precession in sidereal days is
where
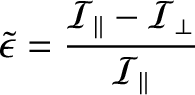
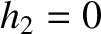 ), the
precession period would be
), the
precession period would be
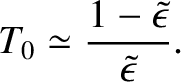
 , we find that
, we find that
 [i.e., the Earth's
dynamical ellipticity is equal to the actual ellipticity due to its slightly flattened shape; see Equations (E.25)–(E.27)] and
[i.e., the Earth's
dynamical ellipticity is equal to the actual ellipticity due to its slightly flattened shape; see Equations (E.25)–(E.27)] and
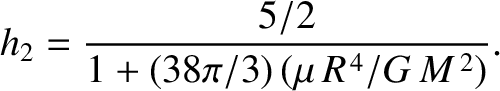
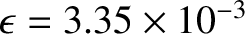 ,
,
 ,
,
 ,
,
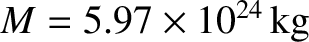 , and
, and
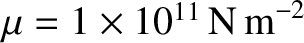 (see Section 6.5), we
deduce that
(see Section 6.5), we
deduce that
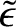
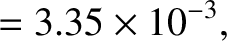
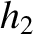
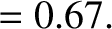


 days (Yoder 1995). Thus, our estimate for the precession period that takes the Earth's lack of
complete rigidity into account is far closer to the correct answer than our estimate that treats the Earth as a completely rigid body.
days (Yoder 1995). Thus, our estimate for the precession period that takes the Earth's lack of
complete rigidity into account is far closer to the correct answer than our estimate that treats the Earth as a completely rigid body.
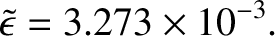
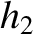 , which is deduced from the measured yielding of the Earth to the Moon's
tidal gravitational field, is
, which is deduced from the measured yielding of the Earth to the Moon's
tidal gravitational field, is