Rotational flattening
Consider the equilibrium configuration of a self-gravitating celestial body,
composed of incompressible fluid, that is rotating
steadily and uniformly
about some fixed axis passing through its center of mass. Let us assume that the outer boundary of the body is spheroidal. (See Section 3.6.)
Let  be the body's total mass,
be the body's total mass,  its mean radius,
its mean radius,
 its ellipticity, and
its ellipticity, and
 its angular rotation velocity. Suppose, finally, that the body's axis of rotation coincides with its axis of symmetry, which is assumed to run along the
its angular rotation velocity. Suppose, finally, that the body's axis of rotation coincides with its axis of symmetry, which is assumed to run along the  -axis.
-axis.
Let us transform to a non-inertial frame of reference that co-rotates with the body about the  -axis, and in which the body consequently appears to be stationary. From Section 6.3,
the problem is now analogous to that of a non-rotating body, except that
the acceleration is written
-axis, and in which the body consequently appears to be stationary. From Section 6.3,
the problem is now analogous to that of a non-rotating body, except that
the acceleration is written
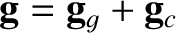 ,
where
,
where
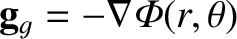 is the gravitational acceleration,
is the gravitational acceleration,
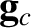 the centrifugal acceleration, and
the centrifugal acceleration, and
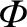 the gravitational potential. The latter acceleration
is of magnitude
the gravitational potential. The latter acceleration
is of magnitude
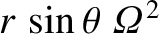 and is everywhere directed
away from the axis of rotation. (See Section 6.3.) Here,
and is everywhere directed
away from the axis of rotation. (See Section 6.3.) Here,  and
and  are spherical coordinates whose origin
is the
body's geometric center and whose
symmetry axis coincides with the axis of rotation.
The centrifugal acceleration is thus
are spherical coordinates whose origin
is the
body's geometric center and whose
symmetry axis coincides with the axis of rotation.
The centrifugal acceleration is thus
 |
(6.33) |
It follows that
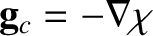 ,
where
,
where
![$\displaystyle \chi(r,\theta) = - \frac{{\mit\Omega}^{\,2}\,r^{\,2}}{2}\,\sin^2\theta= \frac{{\mit\Omega}^{\,2}\,r^{\,2}}{3}\,\left[P_2(\cos\theta)-1\right]$](img1156.png) |
(6.34) |
can be thought of as a sort of centrifugal potential.
Thus, the
total acceleration is
 |
(6.35) |
It is convenient to write the centrifugal potential in the form
![$\displaystyle \chi(r,\theta) = \frac{G\,M}{R}\,\zeta\left(\frac{r}{R}\right)^2\left[P_2(\cos\theta)-1\right],$](img1158.png) |
(6.36) |
where the dimensionless parameter
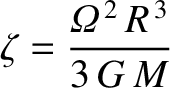 |
(6.37) |
is the typical ratio of the centrifugal acceleration to the gravitational acceleration at  .
Let us assume that this ratio is small; that is,
.
Let us assume that this ratio is small; that is,
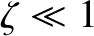 .
.
As before (see Section 3.6), the criterion for an equilibrium state is that the total potential be uniform
over the body's surface, so as to eliminate any tangential forces that
cannot be balanced by internal pressure. Let us assume that the
surface satisfies [see Equation (3.56)]
![$\displaystyle r = R_\theta(\theta) = R\left[1-\frac{2}{3}\,\epsilon\,P_2(\cos\theta)\right],$](img463.png) |
(6.38) |
where
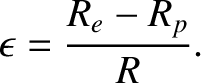 |
(6.39) |
Here,  is the body's mean radius,
is the body's mean radius,
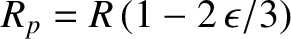 the radius at the poles (i.e., along the axis of rotation), and
the radius at the poles (i.e., along the axis of rotation), and
 the radius at the
equator (i.e., perpendicular to the axis of rotation). See Figure 6.4. It is assumed that
the radius at the
equator (i.e., perpendicular to the axis of rotation). See Figure 6.4. It is assumed that
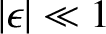 , so that the
body is almost spherical.
The external (to the body) gravitational potential can be written [see Equation (3.66)]
, so that the
body is almost spherical.
The external (to the body) gravitational potential can be written [see Equation (3.66)]
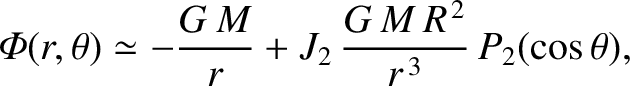 |
(6.40) |
where
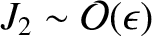 .
The equilibrium configuration is specified by
.
The equilibrium configuration is specified by
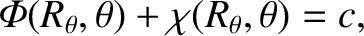 |
(6.41) |
where 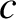 is a constant. It follows from Equations (6.36), (6.38), and (6.40) that, to first order in
is a constant. It follows from Equations (6.36), (6.38), and (6.40) that, to first order in  and
and 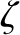 ,
,
![$\displaystyle - \frac{G\,M}{R} \left[1+ \left(\frac{2}{3}\,\epsilon - J_2\right...
...\theta)\right]
+\frac{G\,M}{R} \,\zeta\,\left[P_2(\cos\theta)-1\right]\simeq c,$](img1165.png) |
(6.42) |
which yields
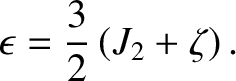 |
(6.43) |
For the special case of a uniform-density body, we have
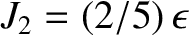 . [See Equation (3.64).]
Hence, the previous equation simplifies to
. [See Equation (3.64).]
Hence, the previous equation simplifies to
 |
(6.44) |
or
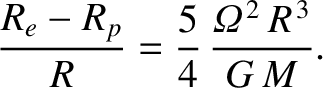 |
(6.45) |
We conclude, from the preceding expression, that the equilibrium configuration
of a (relatively slowly) rotating self-gravitating fluid mass is an oblate spheroid; a sphere
that is slightly flattened along its axis of rotation. The degree of flattening is proportional
to the square of the rotation rate.
Figure 6.4:
Rotational flattening.
|
|
The result of Equation (6.44) was derived on the assumption that there is zero shear stress at the surface of a
uniform-density, rotating, self-gravitating, celestial body. This is certainly true for a fluid body, because fluids (by definition)
are unable to withstand shear stresses. Solids, on the other hand, can withstand
such stresses to a limited extent. Hence, it is not necessarily true that there is zero shear
stress at the surface of a solid rotating body, such as the Earth. Let us investigate whether
expression (6.44) needs to be modified for such a body.
In the presence of the centrifugal potential specified in Equation (6.36), the normal elastic (i.e., non-hydrostatic) stress acting (outward) across the surface  , for a
body of mean radius
, for a
body of mean radius  , ellipticity
, ellipticity  , and uniform density
, and uniform density  ,
can be written
,
can be written
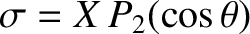 , where [see Equation (C.56)]
, where [see Equation (C.56)]
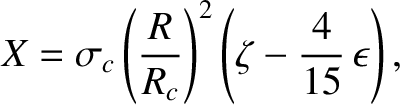 |
(6.46) |
and 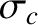 is the yield stress of the material from which the body is composed (i.e., the critical
shear stress above which the material flows like a liquid) (Love 2011). The shear stress is proportional to
is the yield stress of the material from which the body is composed (i.e., the critical
shear stress above which the material flows like a liquid) (Love 2011). The shear stress is proportional to
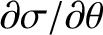 . Furthermore,
. Furthermore,
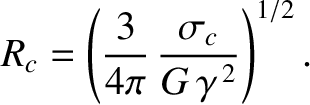 |
(6.47) |
For the rock that makes up the Earth's mantle,
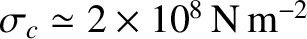 and
and
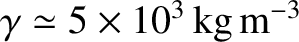 , giving
, giving
 (de Pater and Lissauer 2010.)
Let us assume that
(de Pater and Lissauer 2010.)
Let us assume that  , which implies that, in the absence of the centrifugal
potential, the self-gravity of the body in question
is sufficiently strong to force it to adopt a spherical shape. (See Section 3.6.)
If the surface shear stress is less than the yield stress (i.e., if
, which implies that, in the absence of the centrifugal
potential, the self-gravity of the body in question
is sufficiently strong to force it to adopt a spherical shape. (See Section 3.6.)
If the surface shear stress is less than the yield stress (i.e., if
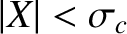 ) then the
body responds elastically to the stress in such a manner that [see Equation (C.57)]
) then the
body responds elastically to the stress in such a manner that [see Equation (C.57)]
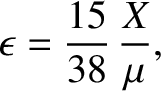 |
(6.48) |
where  is the shear modulus, or rigidity, of the body's constituent material (Love 2011). For the rock that
makes up the Earth's mantle,
is the shear modulus, or rigidity, of the body's constituent material (Love 2011). For the rock that
makes up the Earth's mantle,
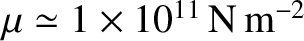 (de Pater and Lissauer 2010).
It follows that
(de Pater and Lissauer 2010).
It follows that
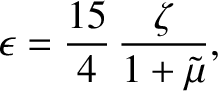 |
(6.49) |
where [see Equation (C.58)]
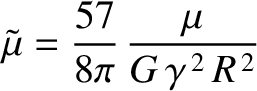 |
(6.50) |
is a dimensionless quantity that is termed the body's effective rigidity.
On the other hand, if the surface shear stress is greater than the yield stress then the
body flows like a liquid until the stress becomes zero. So, it follows from Equation (6.46) that
 |
(6.51) |
which is identical to Equation (6.44). Hence, we deduce that the rotational flattening of a
solid, uniform-density, celestial body is governed by Equation (6.49) if the surface shear
stress does not exceed the yield stress, and by Equation (6.44) otherwise.
In the former case, the condition
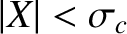 is equivalent to
is equivalent to
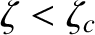 ,
where
,
where
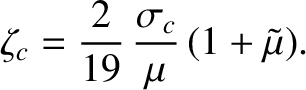 |
(6.52) |
For the rock that makes up the Earth's mantle [for which
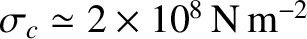 ,
,
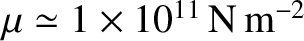 ,
,
 , and
, and
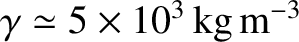 (de Pater and Lissauer 2010)], we find that
(de Pater and Lissauer 2010)], we find that
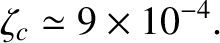 |
(6.53) |
Thus, if
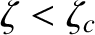 then the
rotational flattening of a uniform body made up of such rock is governed by Equation (6.49), but if
then the
rotational flattening of a uniform body made up of such rock is governed by Equation (6.49), but if
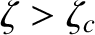 then the
flattening is governed by Equation (6.51).
then the
flattening is governed by Equation (6.51).
Now, for the case of the Earth itself,
 ,
,
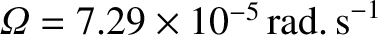 , and
, and
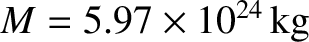 (Yoder 1995).
It follows that
(Yoder 1995).
It follows that
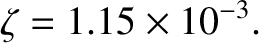 |
(6.54) |
Because
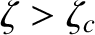 , we deduce that the Earth's centrifugal potential is sufficiently strong to force its constituent
rock to flow like a liquid. Hence, the rotation flattening is governed by Equation (6.51), which
implies that
, we deduce that the Earth's centrifugal potential is sufficiently strong to force its constituent
rock to flow like a liquid. Hence, the rotation flattening is governed by Equation (6.51), which
implies that
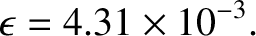 |
(6.55) |
This corresponds to a difference between the Earth's equatorial and polar radii
of
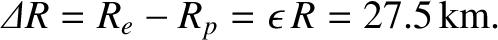 |
(6.56) |
In fact, the observed degree of rotational flattening of the Earth is
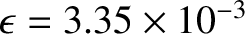 (Yoder 1995),
corresponding to a difference between equatorial and polar radii
of
(Yoder 1995),
corresponding to a difference between equatorial and polar radii
of
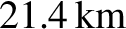 . Our analysis has overestimated the
Earth's rotational flattening because, for the sake of simplicity, we assumed that the terrestrial interior is of uniform density. In reality,
the Earth's core is significantly denser than its crust. (See Section D.6.)
Incidentally, the observed value of the parameter
. Our analysis has overestimated the
Earth's rotational flattening because, for the sake of simplicity, we assumed that the terrestrial interior is of uniform density. In reality,
the Earth's core is significantly denser than its crust. (See Section D.6.)
Incidentally, the observed value of the parameter 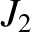 , which measures the strength of the Earth's quadrupole gravitational
field, is
, which measures the strength of the Earth's quadrupole gravitational
field, is
 (Yoder 1995). Hence,
(Yoder 1995). Hence,
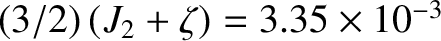 .
In other words, the Earth's rotational flattening satisfies Equation (6.43) extremely accurately. This confirms that although the Earth is not a uniform-density body its response to the centrifugal potential is indeed fluid-like [because Equation (6.43) was derived on the assumption that the
surface of the rotating body in question is in hydrostatic equilibrium in the co-rotating frame].
.
In other words, the Earth's rotational flattening satisfies Equation (6.43) extremely accurately. This confirms that although the Earth is not a uniform-density body its response to the centrifugal potential is indeed fluid-like [because Equation (6.43) was derived on the assumption that the
surface of the rotating body in question is in hydrostatic equilibrium in the co-rotating frame].
Figure: 6.5
Jupiter. Photograph taken by Hubble Space Telescope. A circle is superimposed on the image to make the rotational flattening more clearly visible. The axis of rotation is vertical. Credit: NASA.
|
|
For the planet Jupiter,
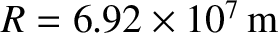 ,
,
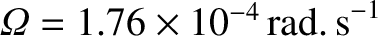 , and
, and
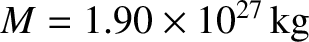 (Yoder 1995; Seidelmann et al. 2007). Hence,
(Yoder 1995; Seidelmann et al. 2007). Hence,
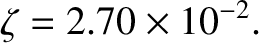 |
(6.57) |
Because Jupiter is largely composed of liquid, its rotation flattening is governed by Equation (6.51),
which yields
 |
(6.58) |
This degree of flattening is much larger than that of the Earth, owing to
Jupiter's relatively large radius (about ten times that of Earth), combined with its relatively
short rotation period (about 0.4 days). In fact, the rotational flattening of
Jupiter is clearly apparent from images of this planet. See Figure 6.5. The observed degree of
rotational flattening of Jupiter is actually
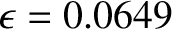 (Yoder 1995). Our estimate for
(Yoder 1995). Our estimate for  is
slightly too large because Jupiter has a mass distribution that is strongly concentrated
at its core. (See Section D.6.) Incidentally, the measured value of
is
slightly too large because Jupiter has a mass distribution that is strongly concentrated
at its core. (See Section D.6.) Incidentally, the measured value of 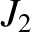 for Jupiter is
for Jupiter is
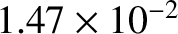 (Yoder 1995).
Hence,
(Yoder 1995).
Hence,
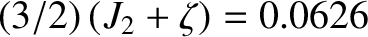 . Thus, Jupiter's rotational flattening also satisfies Equation (6.43)
fairly accurately, confirming that its response to the centrifugal potential is fluid-like.
. Thus, Jupiter's rotational flattening also satisfies Equation (6.43)
fairly accurately, confirming that its response to the centrifugal potential is fluid-like.
 be the body's total mass,
be the body's total mass,  its mean radius,
its mean radius,
 its ellipticity, and
its ellipticity, and
 its angular rotation velocity. Suppose, finally, that the body's axis of rotation coincides with its axis of symmetry, which is assumed to run along the
its angular rotation velocity. Suppose, finally, that the body's axis of rotation coincides with its axis of symmetry, which is assumed to run along the  -axis.
-axis.
 -axis, and in which the body consequently appears to be stationary. From Section 6.3,
the problem is now analogous to that of a non-rotating body, except that
the acceleration is written
-axis, and in which the body consequently appears to be stationary. From Section 6.3,
the problem is now analogous to that of a non-rotating body, except that
the acceleration is written
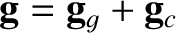 ,
where
,
where
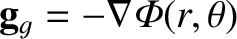 is the gravitational acceleration,
is the gravitational acceleration,
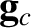 the centrifugal acceleration, and
the centrifugal acceleration, and
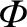 the gravitational potential. The latter acceleration
is of magnitude
the gravitational potential. The latter acceleration
is of magnitude
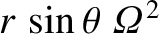 and is everywhere directed
away from the axis of rotation. (See Section 6.3.) Here,
and is everywhere directed
away from the axis of rotation. (See Section 6.3.) Here,  and
and  are spherical coordinates whose origin
is the
body's geometric center and whose
symmetry axis coincides with the axis of rotation.
The centrifugal acceleration is thus
are spherical coordinates whose origin
is the
body's geometric center and whose
symmetry axis coincides with the axis of rotation.
The centrifugal acceleration is thus

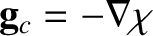 ,
where
can be thought of as a sort of centrifugal potential.
Thus, the
total acceleration is
,
where
can be thought of as a sort of centrifugal potential.
Thus, the
total acceleration is

 .
Let us assume that this ratio is small; that is,
.
Let us assume that this ratio is small; that is,
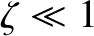 .
.
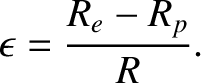
 is the body's mean radius,
is the body's mean radius,
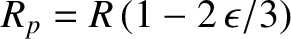 the radius at the poles (i.e., along the axis of rotation), and
the radius at the poles (i.e., along the axis of rotation), and
 the radius at the
equator (i.e., perpendicular to the axis of rotation). See Figure 6.4. It is assumed that
the radius at the
equator (i.e., perpendicular to the axis of rotation). See Figure 6.4. It is assumed that
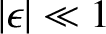 , so that the
body is almost spherical.
The external (to the body) gravitational potential can be written [see Equation (3.66)]
where
, so that the
body is almost spherical.
The external (to the body) gravitational potential can be written [see Equation (3.66)]
where
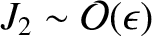 .
The equilibrium configuration is specified by
.
The equilibrium configuration is specified by
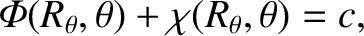
 is a constant. It follows from Equations (6.36), (6.38), and (6.40) that, to first order in
is a constant. It follows from Equations (6.36), (6.38), and (6.40) that, to first order in  and
and 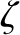 ,
,
![$\displaystyle - \frac{G\,M}{R} \left[1+ \left(\frac{2}{3}\,\epsilon - J_2\right...
...\theta)\right]
+\frac{G\,M}{R} \,\zeta\,\left[P_2(\cos\theta)-1\right]\simeq c,$](img1165.png)
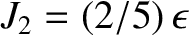 . [See Equation (3.64).]
Hence, the previous equation simplifies to
or
We conclude, from the preceding expression, that the equilibrium configuration
of a (relatively slowly) rotating self-gravitating fluid mass is an oblate spheroid; a sphere
that is slightly flattened along its axis of rotation. The degree of flattening is proportional
to the square of the rotation rate.
. [See Equation (3.64).]
Hence, the previous equation simplifies to
or
We conclude, from the preceding expression, that the equilibrium configuration
of a (relatively slowly) rotating self-gravitating fluid mass is an oblate spheroid; a sphere
that is slightly flattened along its axis of rotation. The degree of flattening is proportional
to the square of the rotation rate.
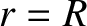 , for a
body of mean radius
, for a
body of mean radius  , ellipticity
, ellipticity  , and uniform density
, and uniform density  ,
can be written
,
can be written
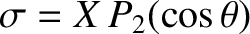 , where [see Equation (C.56)]
, where [see Equation (C.56)]
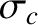 is the yield stress of the material from which the body is composed (i.e., the critical
shear stress above which the material flows like a liquid) (Love 2011). The shear stress is proportional to
is the yield stress of the material from which the body is composed (i.e., the critical
shear stress above which the material flows like a liquid) (Love 2011). The shear stress is proportional to
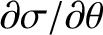 . Furthermore,
. Furthermore,
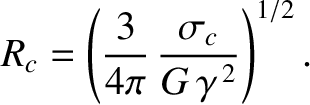
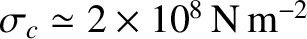 and
and
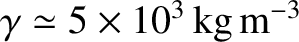 , giving
, giving
 (de Pater and Lissauer 2010.)
Let us assume that
(de Pater and Lissauer 2010.)
Let us assume that  , which implies that, in the absence of the centrifugal
potential, the self-gravity of the body in question
is sufficiently strong to force it to adopt a spherical shape. (See Section 3.6.)
If the surface shear stress is less than the yield stress (i.e., if
, which implies that, in the absence of the centrifugal
potential, the self-gravity of the body in question
is sufficiently strong to force it to adopt a spherical shape. (See Section 3.6.)
If the surface shear stress is less than the yield stress (i.e., if
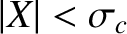 ) then the
body responds elastically to the stress in such a manner that [see Equation (C.57)]
) then the
body responds elastically to the stress in such a manner that [see Equation (C.57)]
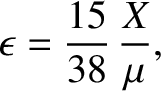
 is the shear modulus, or rigidity, of the body's constituent material (Love 2011). For the rock that
makes up the Earth's mantle,
is the shear modulus, or rigidity, of the body's constituent material (Love 2011). For the rock that
makes up the Earth's mantle,
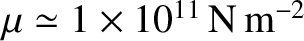 (de Pater and Lissauer 2010).
It follows that
where [see Equation (C.58)]
is a dimensionless quantity that is termed the body's effective rigidity.
On the other hand, if the surface shear stress is greater than the yield stress then the
body flows like a liquid until the stress becomes zero. So, it follows from Equation (6.46) that
which is identical to Equation (6.44). Hence, we deduce that the rotational flattening of a
solid, uniform-density, celestial body is governed by Equation (6.49) if the surface shear
stress does not exceed the yield stress, and by Equation (6.44) otherwise.
In the former case, the condition
(de Pater and Lissauer 2010).
It follows that
where [see Equation (C.58)]
is a dimensionless quantity that is termed the body's effective rigidity.
On the other hand, if the surface shear stress is greater than the yield stress then the
body flows like a liquid until the stress becomes zero. So, it follows from Equation (6.46) that
which is identical to Equation (6.44). Hence, we deduce that the rotational flattening of a
solid, uniform-density, celestial body is governed by Equation (6.49) if the surface shear
stress does not exceed the yield stress, and by Equation (6.44) otherwise.
In the former case, the condition
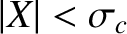 is equivalent to
is equivalent to
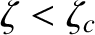 ,
where
,
where
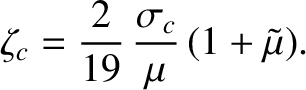
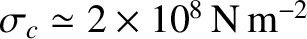 ,
,
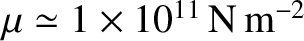 ,
,
 , and
, and
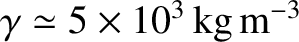 (de Pater and Lissauer 2010)], we find that
(de Pater and Lissauer 2010)], we find that
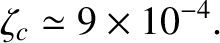
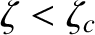 then the
rotational flattening of a uniform body made up of such rock is governed by Equation (6.49), but if
then the
rotational flattening of a uniform body made up of such rock is governed by Equation (6.49), but if
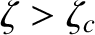 then the
flattening is governed by Equation (6.51).
then the
flattening is governed by Equation (6.51).
 ,
,
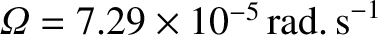 , and
, and
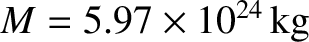 (Yoder 1995).
It follows that
(Yoder 1995).
It follows that
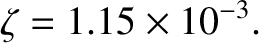
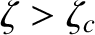 , we deduce that the Earth's centrifugal potential is sufficiently strong to force its constituent
rock to flow like a liquid. Hence, the rotation flattening is governed by Equation (6.51), which
implies that
, we deduce that the Earth's centrifugal potential is sufficiently strong to force its constituent
rock to flow like a liquid. Hence, the rotation flattening is governed by Equation (6.51), which
implies that
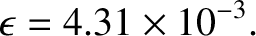
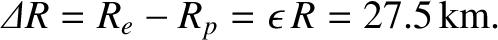
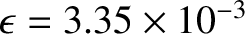 (Yoder 1995),
corresponding to a difference between equatorial and polar radii
of
(Yoder 1995),
corresponding to a difference between equatorial and polar radii
of
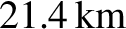 . Our analysis has overestimated the
Earth's rotational flattening because, for the sake of simplicity, we assumed that the terrestrial interior is of uniform density. In reality,
the Earth's core is significantly denser than its crust. (See Section D.6.)
Incidentally, the observed value of the parameter
. Our analysis has overestimated the
Earth's rotational flattening because, for the sake of simplicity, we assumed that the terrestrial interior is of uniform density. In reality,
the Earth's core is significantly denser than its crust. (See Section D.6.)
Incidentally, the observed value of the parameter 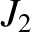 , which measures the strength of the Earth's quadrupole gravitational
field, is
, which measures the strength of the Earth's quadrupole gravitational
field, is
 (Yoder 1995). Hence,
(Yoder 1995). Hence,
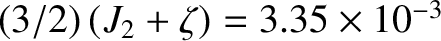 .
In other words, the Earth's rotational flattening satisfies Equation (6.43) extremely accurately. This confirms that although the Earth is not a uniform-density body its response to the centrifugal potential is indeed fluid-like [because Equation (6.43) was derived on the assumption that the
surface of the rotating body in question is in hydrostatic equilibrium in the co-rotating frame].
.
In other words, the Earth's rotational flattening satisfies Equation (6.43) extremely accurately. This confirms that although the Earth is not a uniform-density body its response to the centrifugal potential is indeed fluid-like [because Equation (6.43) was derived on the assumption that the
surface of the rotating body in question is in hydrostatic equilibrium in the co-rotating frame].
![\includegraphics[height=3in]{Chapter05/fig5_05.eps}](img1199.png)
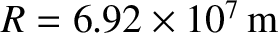 ,
,
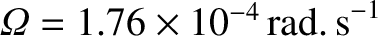 , and
, and
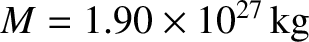 (Yoder 1995; Seidelmann et al. 2007). Hence,
(Yoder 1995; Seidelmann et al. 2007). Hence,
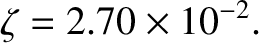

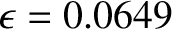 (Yoder 1995). Our estimate for
(Yoder 1995). Our estimate for  is
slightly too large because Jupiter has a mass distribution that is strongly concentrated
at its core. (See Section D.6.) Incidentally, the measured value of
is
slightly too large because Jupiter has a mass distribution that is strongly concentrated
at its core. (See Section D.6.) Incidentally, the measured value of 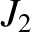 for Jupiter is
for Jupiter is
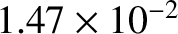 (Yoder 1995).
Hence,
(Yoder 1995).
Hence,
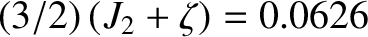 . Thus, Jupiter's rotational flattening also satisfies Equation (6.43)
fairly accurately, confirming that its response to the centrifugal potential is fluid-like.
. Thus, Jupiter's rotational flattening also satisfies Equation (6.43)
fairly accurately, confirming that its response to the centrifugal potential is fluid-like.