Spherical harmonics
The spherical harmonics, denoted
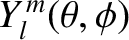 , where
, where 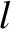 is a non-negative integer, and
is a non-negative integer, and  an integer lying in the range
an integer lying in the range
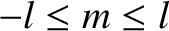 , are the well-behaved solutions to
, are the well-behaved solutions to
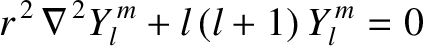 |
(A.159) |
on the surface of a sphere (i.e., 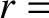 constant). Here,
constant). Here,
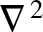 denotes a Laplacian (Riley 1974a), and
denotes a Laplacian (Riley 1974a), and
 ,
,  ,
,  are standard spherical coordinates. The spherical harmonics take the form (Jackson 1975)
are standard spherical coordinates. The spherical harmonics take the form (Jackson 1975)
 |
(A.160) |
where the
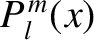 are associated Legendre polynomials (Abramowitz and Stegun 1965a).
In particular,
are associated Legendre polynomials (Abramowitz and Stegun 1965a).
In particular,
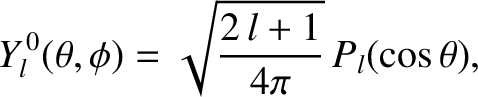 |
(A.161) |
where the 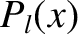 are the Legendre polynomials introduced in Section 3.4. The spherical harmonics satisfy
are the Legendre polynomials introduced in Section 3.4. The spherical harmonics satisfy
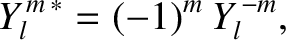 |
(A.162) |
and have the property that they are orthonormal when integrated over the surface of a sphere; that is,
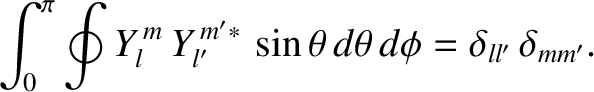 |
(A.163) |
The first few spherical harmonics are:
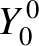 |
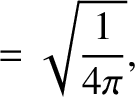 |
(A.164) |
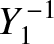 |
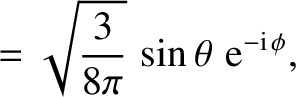 |
(A.165) |
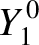 |
 |
(A.166) |
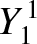 |
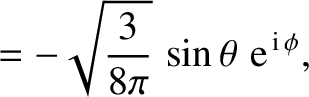 |
(A.167) |
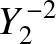 |
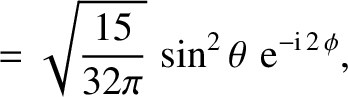 |
(A.168) |
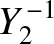 |
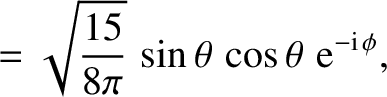 |
(A.169) |
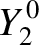 |
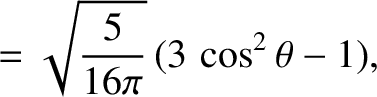 |
(A.170) |
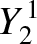 |
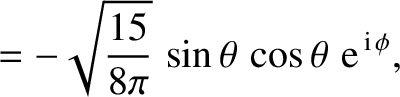 |
(A.171) |
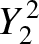 |
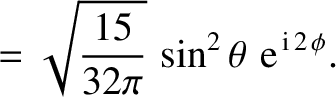 |
(A.172) |
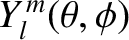 , where
, where 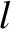 is a non-negative integer, and
is a non-negative integer, and  an integer lying in the range
an integer lying in the range
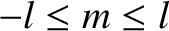 , are the well-behaved solutions to
, are the well-behaved solutions to
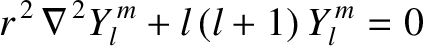
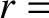 constant). Here,
constant). Here,
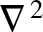 denotes a Laplacian (Riley 1974a), and
denotes a Laplacian (Riley 1974a), and
 ,
,  ,
,  are standard spherical coordinates. The spherical harmonics take the form (Jackson 1975)
are standard spherical coordinates. The spherical harmonics take the form (Jackson 1975)

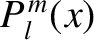 are associated Legendre polynomials (Abramowitz and Stegun 1965a).
In particular,
are associated Legendre polynomials (Abramowitz and Stegun 1965a).
In particular,
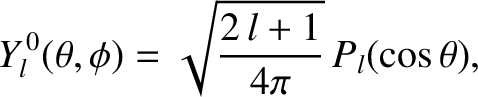
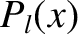 are the Legendre polynomials introduced in Section 3.4. The spherical harmonics satisfy
and have the property that they are orthonormal when integrated over the surface of a sphere; that is,
The first few spherical harmonics are:
are the Legendre polynomials introduced in Section 3.4. The spherical harmonics satisfy
and have the property that they are orthonormal when integrated over the surface of a sphere; that is,
The first few spherical harmonics are: