Next: Transfer orbits Up: Keplerian orbits Previous: Orbital parameters
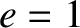 ) or
even hyperbolic (
) or
even hyperbolic (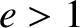 ), as well as elliptical (
), as well as elliptical (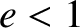 ).
According to Equations (4.5) and (4.13), the total energy per unit mass
of an object in a general orbit around the Sun is
given by
It follows from Equations (4.22), (4.26), and (4.31) that
where
).
According to Equations (4.5) and (4.13), the total energy per unit mass
of an object in a general orbit around the Sun is
given by
It follows from Equations (4.22), (4.26), and (4.31) that
where
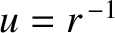 , and
, and
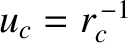 . However, according to Equation (4.30),
. However, according to Equation (4.30),
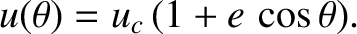 |
(4.43) |
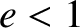 ) have negative total energies,
whereas parabolic orbits (
) have negative total energies,
whereas parabolic orbits (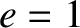 ) have zero total energies,
and hyperbolic orbits (
) have zero total energies,
and hyperbolic orbits (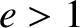 ) have positive total energies. This
makes sense because in a conservative system in which the potential
energy at infinity is set to zero [see Equation (4.4)], we expect bounded orbits to have negative total energies, and unbounded orbits to have positive
total energies. (See Section 2.7.) Thus, elliptical orbits, which are clearly bounded, should indeed have
negative total energies, whereas hyperbolic orbits, which are clearly
unbounded, should indeed have positive total energies. Parabolic orbits
are marginally bounded (i.e., an object executing a parabolic orbit only just manages to escape from the Sun's gravitational field), and thus have zero total energy. For the special case of an elliptical orbit, whose major radius
) have positive total energies. This
makes sense because in a conservative system in which the potential
energy at infinity is set to zero [see Equation (4.4)], we expect bounded orbits to have negative total energies, and unbounded orbits to have positive
total energies. (See Section 2.7.) Thus, elliptical orbits, which are clearly bounded, should indeed have
negative total energies, whereas hyperbolic orbits, which are clearly
unbounded, should indeed have positive total energies. Parabolic orbits
are marginally bounded (i.e., an object executing a parabolic orbit only just manages to escape from the Sun's gravitational field), and thus have zero total energy. For the special case of an elliptical orbit, whose major radius  is finite, we can write
is finite, we can write
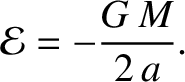 |
(4.45) |