Next: Kepler's first law Up: Keplerian orbits Previous: Plane polar coordinates
 , we obtain
, we obtain
 |
(4.20) |
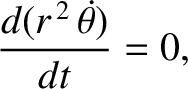 |
(4.21) |
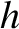 is the magnitude
of the vector
is the magnitude
of the vector 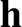 defined in Equation (4.6). Thus, the fact that
defined in Equation (4.6). Thus, the fact that
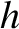 is constant in time is equivalent to the statement that the angular
momentum of our planet is a constant of its motion. As we have already mentioned, this is the case
because gravity is a central force.
is constant in time is equivalent to the statement that the angular
momentum of our planet is a constant of its motion. As we have already mentioned, this is the case
because gravity is a central force.
Suppose that the radius vector connecting our planet to the origin (i.e., the Sun) rotates through an angle
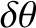 between times
between times 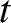 and
and
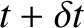 . See Figure 4.2. The approximately triangular region swept out by the radius vector has the area
. See Figure 4.2. The approximately triangular region swept out by the radius vector has the area
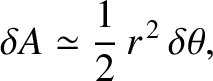 |
(4.23) |
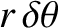 ) times its
height (
) times its
height ( ). Hence, the rate at which the radius vector sweeps out area
is
Thus, the radius vector sweeps out area at a constant rate (because
). Hence, the rate at which the radius vector sweeps out area
is
Thus, the radius vector sweeps out area at a constant rate (because 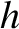 is
constant in time); this is Kepler's second law of planetary motion. We conclude that Kepler's
second law is a direct consequence of angular
momentum conservation.
is
constant in time); this is Kepler's second law of planetary motion. We conclude that Kepler's
second law is a direct consequence of angular
momentum conservation.