Next: Simple harmonic motion Up: Newtonian mechanics Previous: Non-isolated systems
 moving in the
moving in the  -direction, say,
under the action of some
-direction, say,
under the action of some  -directed force
-directed force 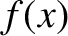 .
Suppose that
.
Suppose that 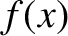 is a conservative force, such as gravity. In this case,
according to Equation (2.19), we can write
where
is a conservative force, such as gravity. In this case,
according to Equation (2.19), we can write
where 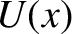 is the potential energy of the particle at position
is the potential energy of the particle at position  .
.
Let the curve 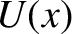 take the form shown in Figure 2.4.
For instance, this curve might represent the gravitational potential energy
of a cyclist freewheeling in a hilly region. Observe that we have set the
potential energy at infinity to zero (which we are generally
free to do, because
potential energy is undefined to an arbitrary additive constant). This is a fairly common convention.
What can we deduce about the motion of the particle in this potential?
take the form shown in Figure 2.4.
For instance, this curve might represent the gravitational potential energy
of a cyclist freewheeling in a hilly region. Observe that we have set the
potential energy at infinity to zero (which we are generally
free to do, because
potential energy is undefined to an arbitrary additive constant). This is a fairly common convention.
What can we deduce about the motion of the particle in this potential?
Well, we know that the total energy,  —which is the sum of the kinetic
energy,
—which is the sum of the kinetic
energy,  , and the potential energy,
, and the potential energy, 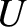 —is a constant of the motion. [See Equation (2.22).]
Hence, we can write
—is a constant of the motion. [See Equation (2.22).]
Hence, we can write
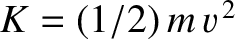 , and neither
, and neither
 nor
nor
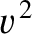 can be negative. Hence, the preceding
expression tells us that the particle's motion is restricted to the
region (or regions) in which the potential energy curve
can be negative. Hence, the preceding
expression tells us that the particle's motion is restricted to the
region (or regions) in which the potential energy curve 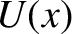 falls
below the value
falls
below the value  . This idea is illustrated in Figure 2.4.
Suppose that the total energy of the system is
. This idea is illustrated in Figure 2.4.
Suppose that the total energy of the system is 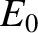 . It is clear, from
the figure, that the particle is trapped inside one or other of the two dips
in the potential; these dips are
generally referred to as potential wells.
Suppose that we now raise the energy to
. It is clear, from
the figure, that the particle is trapped inside one or other of the two dips
in the potential; these dips are
generally referred to as potential wells.
Suppose that we now raise the energy to  . In this
case, the particle is free to enter or leave each of the potential wells, but
its motion is still bounded to some extent, because it clearly cannot move off to
infinity. Finally, let us raise the energy to
. In this
case, the particle is free to enter or leave each of the potential wells, but
its motion is still bounded to some extent, because it clearly cannot move off to
infinity. Finally, let us raise the energy to 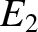 . Now the
particle is unbounded; that is, it can move off to infinity. In conservative systems
in which it makes sense to adopt the convention that the potential
energy at infinity is zero, bounded systems are characterized
by
. Now the
particle is unbounded; that is, it can move off to infinity. In conservative systems
in which it makes sense to adopt the convention that the potential
energy at infinity is zero, bounded systems are characterized
by  , whereas unbounded systems are characterized by
, whereas unbounded systems are characterized by 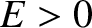 .
.
The preceding discussion suggests that the motion of a particle moving in a potential
generally becomes less bounded as the total energy  of the system increases.
Conversely, we would expect the motion to become more bounded as
of the system increases.
Conversely, we would expect the motion to become more bounded as  decreases.
In fact, if the energy becomes sufficiently small then it appears likely that the
system will settle down in some equilibrium state in which the particle remains stationary.
Let us try to identify any prospective equilibrium states in Figure 2.4.
If the particle remains stationary then it must be subject to zero force (otherwise,
it would accelerate). Hence, according to Equation (2.45), an equilibrium
state is characterized by
decreases.
In fact, if the energy becomes sufficiently small then it appears likely that the
system will settle down in some equilibrium state in which the particle remains stationary.
Let us try to identify any prospective equilibrium states in Figure 2.4.
If the particle remains stationary then it must be subject to zero force (otherwise,
it would accelerate). Hence, according to Equation (2.45), an equilibrium
state is characterized by
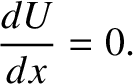 |
(2.47) |
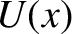 . It can
be seen that the
. It can
be seen that the 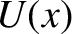 curve shown in Figure 2.4 has
three associated equilibrium states located at
curve shown in Figure 2.4 has
three associated equilibrium states located at
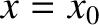 ,
, 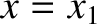 , and
, and 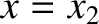 .
.
Let us now make a distinction between stable equilibrium points
and unstable equilibrium points. When the particle is slightly
displaced from a stable equilibrium point then the resultant force acting
on it
must always be such as to return it to this point.
In other words, if 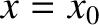 is an equilibrium point then we require
is an equilibrium point then we require
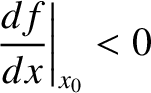 |
(2.48) |
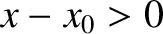 ,
then the force must act to the left, so that
,
then the force must act to the left, so that 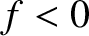 , and vice versa.
Likewise, if
, and vice versa.
Likewise, if
 |
(2.49) |
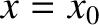 is unstable. It follows, from
Equation (2.45), that stable equilibrium points are
characterized by
is unstable. It follows, from
Equation (2.45), that stable equilibrium points are
characterized by
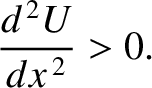 |
(2.50) |
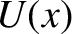 . Likewise, an unstable
equilibrium point corresponds to a maximum of the
. Likewise, an unstable
equilibrium point corresponds to a maximum of the 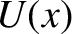 curve. Hence,
we conclude that,
in Figure 2.4,
curve. Hence,
we conclude that,
in Figure 2.4, 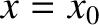 and
and 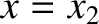 are stable equilibrium points, whereas
are stable equilibrium points, whereas 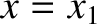 is an unstable equilibrium point.
Of course, this makes perfect sense if we think of
is an unstable equilibrium point.
Of course, this makes perfect sense if we think of 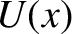 as
a gravitational potential energy curve, so that
as
a gravitational potential energy curve, so that 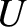 is
directly proportional to height. In this case, all we are saying is that it is
easy to confine a low energy mass at the bottom of a smooth valley,
but it is very difficult to balance the same mass on the top of
a smooth hill (because any slight displacement of the mass will cause it
to slide down the hill). Finally, if
is
directly proportional to height. In this case, all we are saying is that it is
easy to confine a low energy mass at the bottom of a smooth valley,
but it is very difficult to balance the same mass on the top of
a smooth hill (because any slight displacement of the mass will cause it
to slide down the hill). Finally, if
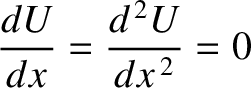 |
(2.51) |
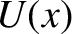 curve. See Figure 2.5.
curve. See Figure 2.5.
The equation of motion of a particle moving in one dimension
under the action of a conservative force is, in principle, integrable. Because
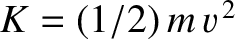 , the energy
conservation equation, Equation (2.46), can be rearranged to give
, the energy
conservation equation, Equation (2.46), can be rearranged to give
![$\displaystyle \varv = \pm\left(\frac{2\,[E-U(x)]}{m}\right)^{1/2},$](img215.png) |
(2.52) |
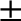 signs correspond to motion to the left and to the right, respectively. However, because
signs correspond to motion to the left and to the right, respectively. However, because
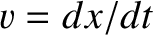 , this expression can be integrated to give
where
, this expression can be integrated to give
where
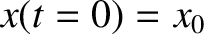 . For sufficiently simple potential functions,
. For sufficiently simple potential functions, 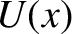 , Equation (2.53) can be solved to give
, Equation (2.53) can be solved to give  as a function of
as a function of 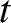 .
For instance, if
.
For instance, if
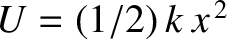 ,
, 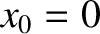 , and the plus sign is chosen, then
, and the plus sign is chosen, then
![$\displaystyle t = \left(\frac{m}{k}\right)^{1/2}\int_0^{(k/2\,E)^{1/2}\,x}\frac...
...c{m}{k}\right)^{1/2} \sin^{-1}\left[\left(\frac{k}{2\,E}\right)^{1/2} x\right],$](img222.png) |
(2.54) |
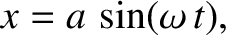 |
(2.55) |
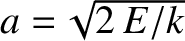 and
and
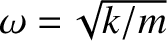 .
Note that the particle reverses direction each time it reaches one of the so-called
turning points (
.
Note that the particle reverses direction each time it reaches one of the so-called
turning points (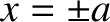 ) at which
) at which 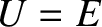 (and, so,
(and, so, 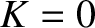 ).
).