Simple harmonic motion
Consider the motion of a point particle of mass  , moving in one dimension, that is
slightly displaced from a stable equilibrium point located at
, moving in one dimension, that is
slightly displaced from a stable equilibrium point located at 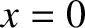 .
Suppose that the particle is moving in the conservative force field
.
Suppose that the particle is moving in the conservative force field 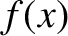 . According to the preceding analysis, in order for
. According to the preceding analysis, in order for 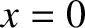 to
correspond to a stable equilibrium point,
we require both
to
correspond to a stable equilibrium point,
we require both
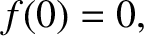 |
(2.56) |
and
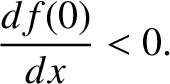 |
(2.57) |
Our particle obeys Newton's second law of motion,
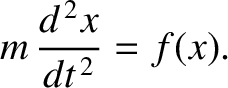 |
(2.58) |
Let us assume that the particle always stays fairly close to its equilibrium
point. In this case, to a good approximation, we can represent 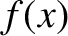 via a truncated Taylor expansion about this point. In other words,
via a truncated Taylor expansion about this point. In other words,
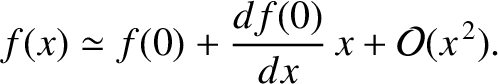 |
(2.59) |
However, according to Equations (2.56) and (2.57), the preceding
expression can be written
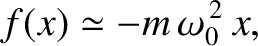 |
(2.60) |
where
 .
Hence, we conclude that our particle satisfies the following approximate
equation of motion,
.
Hence, we conclude that our particle satisfies the following approximate
equation of motion,
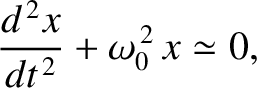 |
(2.61) |
provided that it does not stray too far from its equilibrium point; in other words,
provided 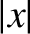 does not become too large.
does not become too large.
Equation (2.61) is called the simple harmonic equation; it
governs the motion of all one-dimensional conservative systems that are slightly
perturbed from some stable equilibrium state. The solution of Equation (2.61)
is well known:
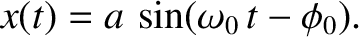 |
(2.62) |
The pattern of motion described by this expression,
which is called simple harmonic motion,
is periodic in time, with repetition period
 , and oscillates between
, and oscillates between 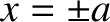 . Here,
. Here,  is called the amplitude of the motion. The parameter
is called the amplitude of the motion. The parameter  ,
known as the phase angle,
simply shifts the pattern of motion backward and forward in time.
Figure 2.6 shows some examples of simple harmonic motion.
Here,
,
known as the phase angle,
simply shifts the pattern of motion backward and forward in time.
Figure 2.6 shows some examples of simple harmonic motion.
Here,
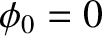 ,
,  , and
, and  correspond to the
solid, short-dashed, and long-dashed curves, respectively.
correspond to the
solid, short-dashed, and long-dashed curves, respectively.
Note that the frequency, 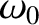 —and, hence, the period,
—and, hence, the period,  —of
simple harmonic motion is determined by the parameters appearing in the simple harmonic equation,
Equation (2.61). However, the amplitude,
—of
simple harmonic motion is determined by the parameters appearing in the simple harmonic equation,
Equation (2.61). However, the amplitude,  , and the phase angle,
, and the phase angle,  ,
are the two integration constants of this second-order ordinary differential
equation, and are thus determined by the initial conditions; that is, the particle's initial displacement and velocity.
,
are the two integration constants of this second-order ordinary differential
equation, and are thus determined by the initial conditions; that is, the particle's initial displacement and velocity.
Figure 2.6:
Simple harmonic motion.
|
|
From Equations (2.45) and (2.60), the potential
energy of our particle at position  is approximately
is approximately
 |
(2.63) |
Hence, the total energy is written
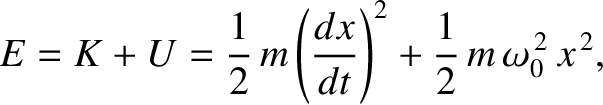 |
(2.64) |
giving
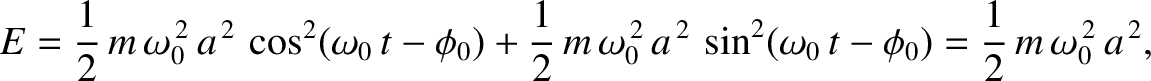 |
(2.65) |
where use has been made of Equation (2.62), and the trigonometric
identity
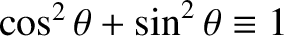 . Note that the
total energy is constant in time, as is to be expected for a
conservative system, and is proportional to the amplitude squared
of the motion.
. Note that the
total energy is constant in time, as is to be expected for a
conservative system, and is proportional to the amplitude squared
of the motion.
Consider the motion of a point particle of mass  that is
slightly displaced from a unstable equilibrium point at
that is
slightly displaced from a unstable equilibrium point at 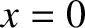 .
The fact that the equilibrium is unstable implies that
.
The fact that the equilibrium is unstable implies that
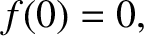 |
(2.66) |
and
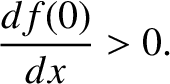 |
(2.67) |
As long as 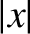 remains small, our particle's equation of motion takes the approximate form
remains small, our particle's equation of motion takes the approximate form
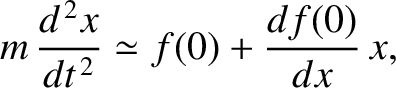 |
(2.68) |
which reduces to
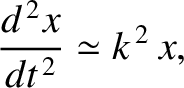 |
(2.69) |
where
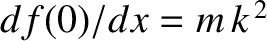 . The most general solution to the preceding equation is
. The most general solution to the preceding equation is
 |
(2.70) |
where  and
and 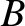 are arbitrary constants. Thus, unless the initial conditions are such that
are arbitrary constants. Thus, unless the initial conditions are such that  is exactly zero, the particle's displacement
from the unstable equilibrium point grows exponentially in time.
is exactly zero, the particle's displacement
from the unstable equilibrium point grows exponentially in time.
 , moving in one dimension, that is
slightly displaced from a stable equilibrium point located at
, moving in one dimension, that is
slightly displaced from a stable equilibrium point located at 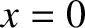 .
Suppose that the particle is moving in the conservative force field
.
Suppose that the particle is moving in the conservative force field 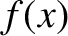 . According to the preceding analysis, in order for
. According to the preceding analysis, in order for 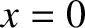 to
correspond to a stable equilibrium point,
we require both
and
Our particle obeys Newton's second law of motion,
to
correspond to a stable equilibrium point,
we require both
and
Our particle obeys Newton's second law of motion,
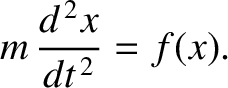
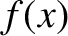 via a truncated Taylor expansion about this point. In other words,
via a truncated Taylor expansion about this point. In other words,
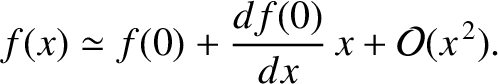
 .
Hence, we conclude that our particle satisfies the following approximate
equation of motion,
provided that it does not stray too far from its equilibrium point; in other words,
provided
.
Hence, we conclude that our particle satisfies the following approximate
equation of motion,
provided that it does not stray too far from its equilibrium point; in other words,
provided 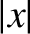 does not become too large.
does not become too large.
 , and oscillates between
, and oscillates between 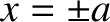 . Here,
. Here,  is called the amplitude of the motion. The parameter
is called the amplitude of the motion. The parameter  ,
known as the phase angle,
simply shifts the pattern of motion backward and forward in time.
Figure 2.6 shows some examples of simple harmonic motion.
Here,
,
known as the phase angle,
simply shifts the pattern of motion backward and forward in time.
Figure 2.6 shows some examples of simple harmonic motion.
Here,
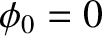 ,
,  , and
, and  correspond to the
solid, short-dashed, and long-dashed curves, respectively.
correspond to the
solid, short-dashed, and long-dashed curves, respectively.
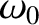 —and, hence, the period,
—and, hence, the period,  —of
simple harmonic motion is determined by the parameters appearing in the simple harmonic equation,
Equation (2.61). However, the amplitude,
—of
simple harmonic motion is determined by the parameters appearing in the simple harmonic equation,
Equation (2.61). However, the amplitude,  , and the phase angle,
, and the phase angle,  ,
are the two integration constants of this second-order ordinary differential
equation, and are thus determined by the initial conditions; that is, the particle's initial displacement and velocity.
,
are the two integration constants of this second-order ordinary differential
equation, and are thus determined by the initial conditions; that is, the particle's initial displacement and velocity.
 is approximately
is approximately

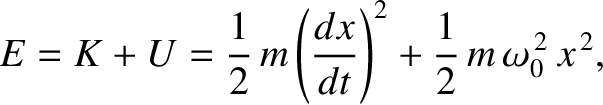
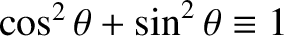 . Note that the
total energy is constant in time, as is to be expected for a
conservative system, and is proportional to the amplitude squared
of the motion.
. Note that the
total energy is constant in time, as is to be expected for a
conservative system, and is proportional to the amplitude squared
of the motion.
 that is
slightly displaced from a unstable equilibrium point at
that is
slightly displaced from a unstable equilibrium point at 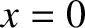 .
The fact that the equilibrium is unstable implies that
.
The fact that the equilibrium is unstable implies that
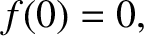
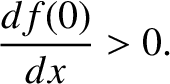
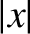 remains small, our particle's equation of motion takes the approximate form
remains small, our particle's equation of motion takes the approximate form
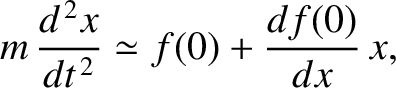
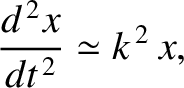
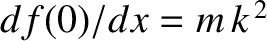 . The most general solution to the preceding equation is
. The most general solution to the preceding equation is

 and
and 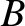 are arbitrary constants. Thus, unless the initial conditions are such that
are arbitrary constants. Thus, unless the initial conditions are such that  is exactly zero, the particle's displacement
from the unstable equilibrium point grows exponentially in time.
is exactly zero, the particle's displacement
from the unstable equilibrium point grows exponentially in time.