Next: Exercises Up: Newtonian mechanics Previous: Simple harmonic motion
 and is located
at position vector
and is located
at position vector 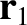 . Likewise, the second object
is of mass
. Likewise, the second object
is of mass 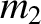 and is located at position vector
and is located at position vector 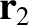 .
Let the first object exert a force
.
Let the first object exert a force
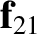 on the
second. By Newton's third law, the second object exerts an
equal and opposite force,
on the
second. By Newton's third law, the second object exerts an
equal and opposite force,
 , on the
first. Suppose that there are no other forces in the problem. The equations of motion of our two objects are thus
where
, on the
first. Suppose that there are no other forces in the problem. The equations of motion of our two objects are thus
where
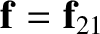 .
.
Now, the center of mass of our system is located at
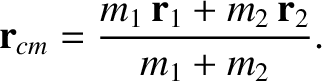 |
(2.73) |
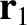 |
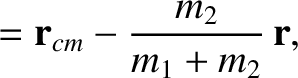 |
(2.74) |
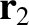 |
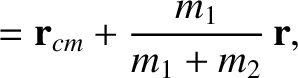 |
(2.75) |
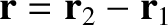 . See Figure 2.7.
Substituting the preceding two equations into Equations (2.71) and (2.72),
and making use of the fact that the center of mass of an isolated system
does not accelerate (see Section 2.5), we find that both equations yield
where
. See Figure 2.7.
Substituting the preceding two equations into Equations (2.71) and (2.72),
and making use of the fact that the center of mass of an isolated system
does not accelerate (see Section 2.5), we find that both equations yield
where
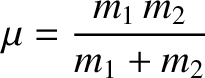 |
(2.77) |
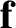 is the same as that acting on both objects in the original problem (except for a minus sign); however, the mass,
is the same as that acting on both objects in the original problem (except for a minus sign); however, the mass,  , is different, and
is less than either of
, is different, and
is less than either of  or
or 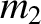 (which is why it is called the “reduced” mass).
We conclude that the dynamics of an isolated system consisting of two interacting point objects can
always be reduced to that of an equivalent system consisting of a single point object moving in a fixed force field.
(which is why it is called the “reduced” mass).
We conclude that the dynamics of an isolated system consisting of two interacting point objects can
always be reduced to that of an equivalent system consisting of a single point object moving in a fixed force field.