Next: Non-isolated systems Up: Newtonian mechanics Previous: Newton's second law of
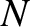 mutually interacting point objects.
Let the
mutually interacting point objects.
Let the  th object, whose mass is
th object, whose mass is 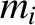 , be located at position vector
, be located at position vector 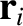 .
Suppose that this object exerts a force
.
Suppose that this object exerts a force
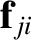 on the
on the 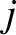 th object.
Likewise, suppose that the
th object.
Likewise, suppose that the 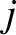 th object exerts a force
th object exerts a force
 on the
on the
 th object.
Newton's third
law of motion essentially states that these two forces are equal and opposite, irrespective
of their nature.
In other words,
See Figure 2.2.
One corollary of Newton's third law is that an object cannot exert
a force on itself. Another corollary is that all forces in the universe have corresponding reactions. The only exceptions to this
rule are the fictitious forces that arise in non-inertial reference frames (e.g., the centrifugal and Coriolis
forces that appear in rotating reference frames; see Chapter 6). Fictitious forces do not generally possess reactions.
th object.
Newton's third
law of motion essentially states that these two forces are equal and opposite, irrespective
of their nature.
In other words,
See Figure 2.2.
One corollary of Newton's third law is that an object cannot exert
a force on itself. Another corollary is that all forces in the universe have corresponding reactions. The only exceptions to this
rule are the fictitious forces that arise in non-inertial reference frames (e.g., the centrifugal and Coriolis
forces that appear in rotating reference frames; see Chapter 6). Fictitious forces do not generally possess reactions.
Newton's third law implies action at a
distance. In other words, if the force that object
 exerts on object
exerts on object 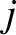 suddenly changes then Newton's third law
demands that there must be an immediate
change in the force that object
suddenly changes then Newton's third law
demands that there must be an immediate
change in the force that object
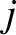 exerts on object
exerts on object  . Moreover, this must be true irrespective of the
distance between the two objects. However, we now know that
Einstein's special theory of relativity forbids information from traveling through the
universe faster than the velocity of light in vacuum (Rindler 1977). Hence, action at a distance is also forbidden. In other words, if the force that object
. Moreover, this must be true irrespective of the
distance between the two objects. However, we now know that
Einstein's special theory of relativity forbids information from traveling through the
universe faster than the velocity of light in vacuum (Rindler 1977). Hence, action at a distance is also forbidden. In other words, if the force that object
 exerts on object
exerts on object 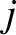 suddenly changes then there must be a
time delay, which is at least as long as it takes a light ray to propagate
between the two objects, before the force that object
suddenly changes then there must be a
time delay, which is at least as long as it takes a light ray to propagate
between the two objects, before the force that object
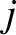 exerts on object
exerts on object  can respond. Of course, this implies that
Newton's third law is not, strictly speaking, correct. However, as
long as we restrict our investigations to the motions of dynamical
systems over timescales that are long compared to the time
required for light rays to traverse these systems, Newton's third
law can be regarded as being approximately correct.
can respond. Of course, this implies that
Newton's third law is not, strictly speaking, correct. However, as
long as we restrict our investigations to the motions of dynamical
systems over timescales that are long compared to the time
required for light rays to traverse these systems, Newton's third
law can be regarded as being approximately correct.
In an inertial frame, Newton's second law of motion applied to the  th object yields
th object yields
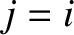 , because the
, because the  th object cannot exert a force on itself. Let us now take this
equation and sum it over all objects. We obtain
Consider the sum over forces on the right-hand side of the preceding equation.
Each element of this sum—
th object cannot exert a force on itself. Let us now take this
equation and sum it over all objects. We obtain
Consider the sum over forces on the right-hand side of the preceding equation.
Each element of this sum—
 , say—can be paired with another element—
, say—can be paired with another element—
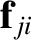 ,
in this case—which is equal and opposite, according to Newton's third law. In other words,
the elements of the sum all cancel out in pairs. Thus, the net value of the sum is zero.
It follows that Equation (2.25) can be written
where
,
in this case—which is equal and opposite, according to Newton's third law. In other words,
the elements of the sum all cancel out in pairs. Thus, the net value of the sum is zero.
It follows that Equation (2.25) can be written
where
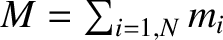 is the total mass. The quantity
is the total mass. The quantity
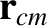 is the vector displacement of the center of mass of
the system, which is an imaginary point whose coordinates are the mass-weighted
averages of the coordinates of the objects that constitute the system:
According to Equation (2.26), the center of mass of the
system moves uniformly in a straight line, in accordance with
Newton's first law of motion, irrespective of the nature of the
forces acting between the various components of the system.
is the vector displacement of the center of mass of
the system, which is an imaginary point whose coordinates are the mass-weighted
averages of the coordinates of the objects that constitute the system:
According to Equation (2.26), the center of mass of the
system moves uniformly in a straight line, in accordance with
Newton's first law of motion, irrespective of the nature of the
forces acting between the various components of the system.
Now, if the center of mass moves uniformly in a straight line then the center of mass velocity,
is a constant of the motion. However, the momentum of the th object takes the
form
th object takes the
form
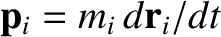 . Hence, the total momentum of the
system is written
A comparison of Equations (2.28) and (2.29) suggests that
. Hence, the total momentum of the
system is written
A comparison of Equations (2.28) and (2.29) suggests that 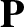 is also
a constant of the motion. In other words, the total momentum
of the system is a conserved quantity, irrespective of the nature of the
forces acting between the various components of the system. This result (which only holds if there is zero net external force acting on the system) is
a direct consequence of Newton's third law of motion.
is also
a constant of the motion. In other words, the total momentum
of the system is a conserved quantity, irrespective of the nature of the
forces acting between the various components of the system. This result (which only holds if there is zero net external force acting on the system) is
a direct consequence of Newton's third law of motion.
Taking the vector product of Equation (2.24) with the position vector 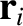 , we
obtain
, we
obtain
 as a result of the forces exerted on it by the other objects.
It is easily seen that
as a result of the forces exerted on it by the other objects.
It is easily seen that
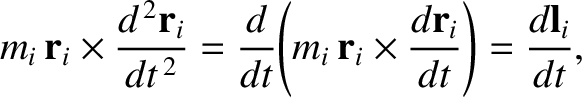 |
(2.31) |
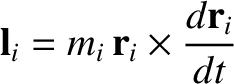 |
(2.32) |
 th object about the origin
of our coordinate system.
Moreover, the total angular momentum of the system (about the origin) takes the form
th object about the origin
of our coordinate system.
Moreover, the total angular momentum of the system (about the origin) takes the form
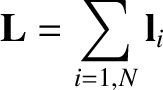 |
(2.33) |
Consider the sum on the right-hand side of Equation (2.34). A general term,
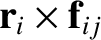 , in this sum can always be paired with a
matching term,
, in this sum can always be paired with a
matching term,
 , in which the indices have been swapped.
Making use of Equation (2.23), we can write the sum of a general matched pair as
, in which the indices have been swapped.
Making use of Equation (2.23), we can write the sum of a general matched pair as
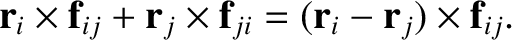 |
(2.35) |
 is parallel
to
is parallel
to
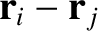 . In other words, the force exerted on object
. In other words, the force exerted on object 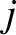 by object
by object  either points directly toward, or directly away from, object
either points directly toward, or directly away from, object  ,
and vice versa. See Figure 2.3.
This is a reasonable assumption,
because virtually all of the forces that we encounter in celestial mechanics are of this type (e.g., gravity).
It follows that if the forces are central then the vector product
on the right-hand side of the previous expression is zero.
We conclude that
,
and vice versa. See Figure 2.3.
This is a reasonable assumption,
because virtually all of the forces that we encounter in celestial mechanics are of this type (e.g., gravity).
It follows that if the forces are central then the vector product
on the right-hand side of the previous expression is zero.
We conclude that
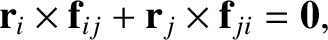 |
(2.36) |
 and
and 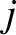 . Thus, the sum on the right-hand side of Equation (2.34) is zero for any kind of central force. We are left with
In other words, the total angular momentum of the system is
a conserved quantity, provided that the different components of the
system interact via central forces (and there is zero net external torque
acting on the system).
. Thus, the sum on the right-hand side of Equation (2.34) is zero for any kind of central force. We are left with
In other words, the total angular momentum of the system is
a conserved quantity, provided that the different components of the
system interact via central forces (and there is zero net external torque
acting on the system).