Next: Orbital energies Up: Keplerian orbits Previous: Kepler's third law
 , is simply the mean of the perihelion
and aphelion distances,
, is simply the mean of the perihelion
and aphelion distances,
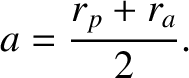 |
(4.36) |
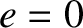 corresponds to a circular orbit, whereas
corresponds to a circular orbit, whereas
 corresponds to an infinitely elongated elliptical orbit. Note that the Sun is displaced a
distance
corresponds to an infinitely elongated elliptical orbit. Note that the Sun is displaced a
distance 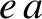 along the major axis from the geometric center of the orbit. (See Section A.9 and Figure 4.3.)
along the major axis from the geometric center of the orbit. (See Section A.9 and Figure 4.3.)
![\includegraphics[height=1.75in]{Chapter03/fig3_03.eps}](img643.png)
|
As is easily demonstrated from the preceding analysis, Kepler laws of planetary motion can be written in the convenient form
where is the mean orbital radius (i.e., the major radius),
is the mean orbital radius (i.e., the major radius),  the orbital eccentricity, and
the orbital eccentricity, and
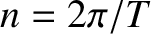 the mean orbital angular velocity.
the mean orbital angular velocity.