Next: Annual equation Up: Lunar motion Previous: Solution of lunar equations
 .
.
According to Equations (11.131) and (11.143),
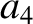 |
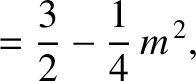 |
(11.215) |
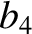 |
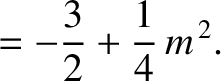 |
(11.216) |
According to Equations (11.132) and (11.144),
 |
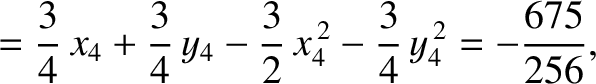 |
(11.219) |
 |
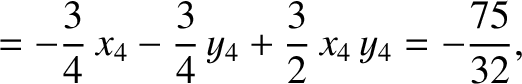 |
(11.220) |
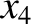 and
and 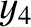 . It follows from Equations (11.192), (11.193), and (11.198) that
. It follows from Equations (11.192), (11.193), and (11.198) that
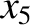 |
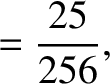 |
(11.221) |
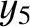 |
 |
(11.222) |
Finally, according to Equation (11.125),
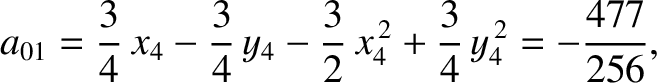 |
(11.223) |
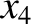 and
and 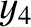 . Equation (11.189) yields
. Equation (11.189) yields
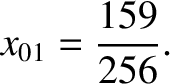 |
(11.224) |
It follows from Equations (11.122)–(11.124), (11.157), (11.163), (11.164), (11.175), and (11.176), as well as the previous expressions for 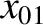 ,
, 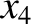 ,
, 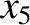 ,
, 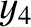 , and
, and 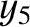 , that the net perturbation of the lunar orbit
due to terms in the solution of the lunar equations of motion that depend only on
, that the net perturbation of the lunar orbit
due to terms in the solution of the lunar equations of motion that depend only on  is
is
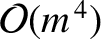 .
.
The first term on the right-hand side of Equation (11.226) is known as
variation, and is clearly due to the perturbing influence of the Sun (because it depends only on the parameter  ,
which is a measure of this influence). Variation attains its maximal
amplitude around the so-called octant points, at which the
Moon's disk is either one-quarter or three-quarters illuminated (i.e., when
,
which is a measure of this influence). Variation attains its maximal
amplitude around the so-called octant points, at which the
Moon's disk is either one-quarter or three-quarters illuminated (i.e., when
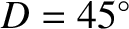 ,
, 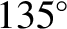 ,
,
 , or
, or 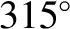 ). Conversely, the amplitude of variation is zero around the so-called quadrant points,
at which the Moon's disk is either fully illuminated, half illuminated, or not illuminated at all (i.e., when
). Conversely, the amplitude of variation is zero around the so-called quadrant points,
at which the Moon's disk is either fully illuminated, half illuminated, or not illuminated at all (i.e., when 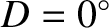 ,
, 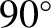 ,
,
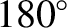 , or
, or 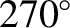 ). Variation generates a perturbation in the lunar ecliptic longitude that oscillates sinusoidally with a period of half a synodic month.11.2 This oscillation period is in good agreement
with observations. However, according to Equation (11.226), the amplitude of the oscillation (calculated using
). Variation generates a perturbation in the lunar ecliptic longitude that oscillates sinusoidally with a period of half a synodic month.11.2 This oscillation period is in good agreement
with observations. However, according to Equation (11.226), the amplitude of the oscillation (calculated using 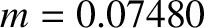 ) is
) is 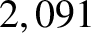 arc seconds, which is somewhat less than the observed amplitude of
arc seconds, which is somewhat less than the observed amplitude of 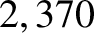 arc seconds (Chapront-Touzé and Chapront 1988). This discrepancy between
theory and observation is due to the fact that, for the sake of simplicity, our expression for variation only includes contributions that are fourth order, or less, in the small parameter
arc seconds (Chapront-Touzé and Chapront 1988). This discrepancy between
theory and observation is due to the fact that, for the sake of simplicity, our expression for variation only includes contributions that are fourth order, or less, in the small parameter  .
.
Equations (11.103) and (11.225) imply that the mean radius of the lunar orbit is
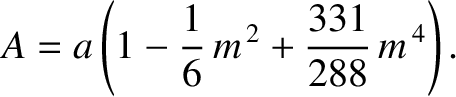 |
(11.228) |
 is the effective major radius of the orbit.
Likewise,
Equations (11.97), (11.104), and (11.226) suggest that the mean orbital angular velocity of the Moon is
is the effective major radius of the orbit.
Likewise,
Equations (11.97), (11.104), and (11.226) suggest that the mean orbital angular velocity of the Moon is
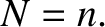 |
(11.229) |
 is the mass of the Earth, and
is the mass of the Earth, and  the mass of the Moon. The previous expression is accurate to
the mass of the Moon. The previous expression is accurate to
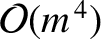 .
Equation (11.230) implies that, when applied to the geocentric lunar orbit, Kepler's third law of orbital motion (see Sections 4.7 and 4.16) is slightly modified by the
perturbing influence of the Sun (which is parameterized by
.
Equation (11.230) implies that, when applied to the geocentric lunar orbit, Kepler's third law of orbital motion (see Sections 4.7 and 4.16) is slightly modified by the
perturbing influence of the Sun (which is parameterized by  ).
).