Next: Solution of lunar equations Up: Lunar motion Previous: Derivation of lunar equations
 , and which moves at a
steady angular velocity equal to the Moon's mean orbital angular velocity,
, and which moves at a
steady angular velocity equal to the Moon's mean orbital angular velocity,  . Likewise, the
mean sun is a second imaginary body that executes a circular orbit about the Earth–Moon barycenter, in the ecliptic plane, whose radius is equal to the mean
radius of the Sun's (apparent) orbit,
. Likewise, the
mean sun is a second imaginary body that executes a circular orbit about the Earth–Moon barycenter, in the ecliptic plane, whose radius is equal to the mean
radius of the Sun's (apparent) orbit, 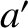 , and which moves at a
steady angular velocity equal to the Sun's mean orbital angular velocity,
, and which moves at a
steady angular velocity equal to the Sun's mean orbital angular velocity, 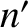 . Thus, the
“geocentric” ecliptic longitudes of the mean moon and the mean sun are
. Thus, the
“geocentric” ecliptic longitudes of the mean moon and the mean sun are
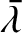 |
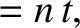 |
(11.97) |
 |
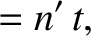 |
(11.98) |
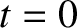 .
.
The following definitions are useful. The lunar mean anomaly,
is defined as the angular distance (in geocentric ecliptic longitude) between the mean moon and the lunar perigee. Here, is the ecliptic longitude of the lunar perigee.
The lunar mean argument of latitude,
is the ecliptic longitude of the lunar perigee.
The lunar mean argument of latitude,
 |
(11.100) |
 is the ecliptic longitude of the lunar ascending node.
The lunar mean elongation from the Sun,
is the ecliptic longitude of the lunar ascending node.
The lunar mean elongation from the Sun,
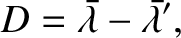 |
(11.101) |
Finally, it is convenient to define
Thus,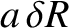 is the difference between the radial distance of the Moon from the Earth and that of the mean moon from the Earth,
is the difference between the radial distance of the Moon from the Earth and that of the mean moon from the Earth,
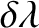 is the difference between the geocentric ecliptic longitudes of the Moon and the mean moon, and
is the difference between the geocentric ecliptic longitudes of the Moon and the mean moon, and
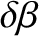 is the
difference between the geocentric ecliptic latitudes of the Moon and the mean moon.
is the
difference between the geocentric ecliptic latitudes of the Moon and the mean moon.