- 2.1
- An excellent discussion of the historical
development of Newtonian mechanics, as well as the physical and
philosophical assumptions which underpin this theory, is
given in Barbour 2001.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.2
- A scalar is a physical quantity that is invariant under
rotation of the coordinate axes. A vector is a physical quantity that transforms in an analogous manner to
a displacement under rotation of the coordinate axes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 5.1
- Precession can be either prograde (in the same sense as
orbital motion) or retrograde (in the opposite sense). Retrograde precession is often called regression.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 6.1
- Actually, the Earth's rotation period relative to the distant stars is called a stellar day,
whereas a sidereal day refers to the Earth's rotation period relative to the vernal equinox (which is a misnomer, because “sidereal” means stellar.) A sidereal day is approximately
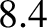 ms less than a solar day, so the distinction between the two is irrelevant for most purposes.
ms less than a solar day, so the distinction between the two is irrelevant for most purposes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 10.1
- In mathematical terminology, two curves are said to osculate when they touch one another so as to have a common tangent at the point of contact. From the Latin osculatus, “kissed.”
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 11.1
- This precession rate is about
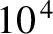 times greater than any of the planetary perihelion precession
rates discussed in Sections 5.4 and 10.3.
times greater than any of the planetary perihelion precession
rates discussed in Sections 5.4 and 10.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 11.2
- A
synodic month, which is
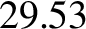 days, is the mean period between successive new moons.
days, is the mean period between successive new moons.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
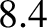 ms less than a solar day, so the distinction between the two is irrelevant for most purposes.
ms less than a solar day, so the distinction between the two is irrelevant for most purposes.
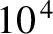 times greater than any of the planetary perihelion precession
rates discussed in Sections 5.4 and 10.3.
times greater than any of the planetary perihelion precession
rates discussed in Sections 5.4 and 10.3.
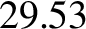 days, is the mean period between successive new moons.
days, is the mean period between successive new moons.