Next: Secular evolution of planetary Up: Secular perturbation theory Previous: Introduction
 and position
vector
and position
vector 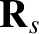 . Likewise, let the two planets have masses
. Likewise, let the two planets have masses 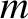 and
and 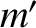 and position vectors
and position vectors 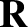 and
and 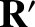 , respectively. Here, we are
assuming that
, respectively. Here, we are
assuming that
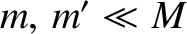 . Finally, let
. Finally, let
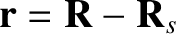 and
and
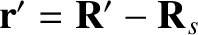 be the position vector of each planet
relative to the Sun. Without loss of generality, we can assume that
be the position vector of each planet
relative to the Sun. Without loss of generality, we can assume that 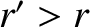 .
.
In an inertial reference frame, the equations of motion of the various elements of our simplified solar system are
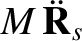 |
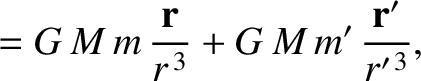 |
(10.1) |
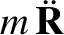 |
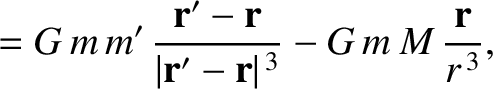 |
(10.2) |
 |
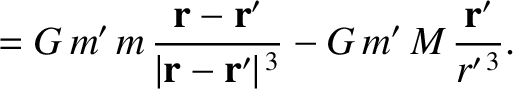 |
(10.3) |
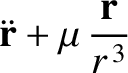 |
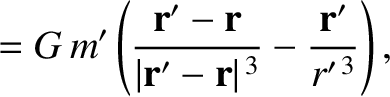 |
(10.4) |
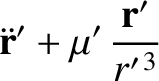 |
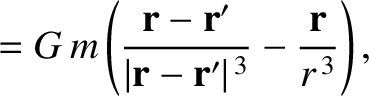 |
(10.5) |
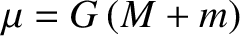 and
and
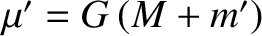 . The right-hand
sides of these equations specify the interplanetary interaction forces that were neglected in our previous analysis. These right-hand
sides can be conveniently expressed as the gradients of potentials:
where
with
. The right-hand
sides of these equations specify the interplanetary interaction forces that were neglected in our previous analysis. These right-hand
sides can be conveniently expressed as the gradients of potentials:
where
with
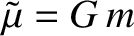 , and
, and
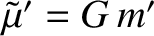 . Here,
. Here,
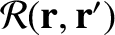 and
and
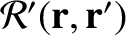 are termed disturbing functions. Moreover,
are termed disturbing functions. Moreover,  and
and  are the gradient operators involving the
unprimed and primed coordinates, respectively.
are the gradient operators involving the
unprimed and primed coordinates, respectively.
In the absence of the second planet, the orbit of the first planet is fully described by its
six standard orbital elements (which are constants of its motion): the major radius,  ; the mean longitude at epoch,
; the mean longitude at epoch,
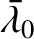 ; the eccentricity,
; the eccentricity, 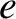 ;
the inclination (to the ecliptic plane),
;
the inclination (to the ecliptic plane), 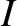 ; the longitude of the perihelion,
; the longitude of the perihelion,
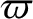 ; and the longitude of the ascending node,
; and the longitude of the ascending node,
 . (See Section 4.12.) As described in Appendix G, the perturbing influence of the second planet
causes these elements to slowly evolve in time. Such time-varying orbital elements are generally known as osculating
elements.10.1
Actually, when describing the aforementioned evolution, it is more convenient to
work in terms of an alternative set of osculating elements, namely,
. (See Section 4.12.) As described in Appendix G, the perturbing influence of the second planet
causes these elements to slowly evolve in time. Such time-varying orbital elements are generally known as osculating
elements.10.1
Actually, when describing the aforementioned evolution, it is more convenient to
work in terms of an alternative set of osculating elements, namely,
![$a(t)=a^{(0)}[1+\epsilon'\,a^{(1)}(t)]$](img2428.png) ,
,
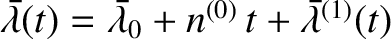 ,
,
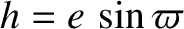 ,
,
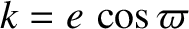 ,
,
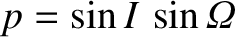 , and
, and
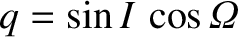 . Here,
. Here,
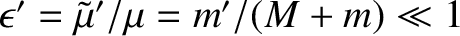 and
and
![$n(t)=n^{(0)}[1-(3/2)\,\epsilon'\,a^{(1)}(t)]$](img2435.png) , where
, where
![$n^{(0)}=(\mu/[a^{(0)}]^3)^{1/2}$](img2436.png) is the unperturbed mean
orbital angular velocity. In the following, for ease of notation,
is the unperturbed mean
orbital angular velocity. In the following, for ease of notation, 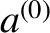 and
and 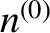 are written simply as
are written simply as  and
and 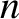 , respectively. Furthermore,
, respectively. Furthermore,
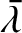 will be used as shorthand for
will be used as shorthand for
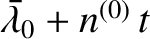 .
The evolution equations for the first planet's osculating orbital elements
take the form (see Section H.2)
.
The evolution equations for the first planet's osculating orbital elements
take the form (see Section H.2)
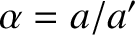 ,
,
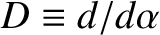 , and
, and
![$\displaystyle b_s^{(j)}(\alpha) = \frac{1}{\pi}\int_0^{2\pi}\frac{\cos(j\,\psi)\,d\psi}{[1-2\,\alpha\,\cos\psi+\alpha^{\,2}]^s},$](img2467.png) |
(10.19) |
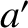 ,
,
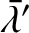 ,
, 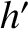 ,
, 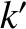 ,
, 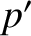 ,
, 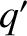 are the osculating orbital elements of the second planet.
The
are the osculating orbital elements of the second planet.
The 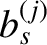 factors are known as Laplace coefficients (Brouwer and Clemence 1961).
In deriving these expressions from Equations (10.6) and (10.8), we have expanded to first order in the ratio of the planetary masses to the
solar mass; we have then evaluated the secular terms in the disturbing
functions (i.e., the terms that are independent of
factors are known as Laplace coefficients (Brouwer and Clemence 1961).
In deriving these expressions from Equations (10.6) and (10.8), we have expanded to first order in the ratio of the planetary masses to the
solar mass; we have then evaluated the secular terms in the disturbing
functions (i.e., the terms that are independent of
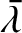 and
and
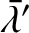 ) to second order in the orbital eccentricities and inclinations. The nonsecular terms in the disturbing functions are
evaluated to first order in the
eccentricities and inclinations. (See Appendix H.) This expansion procedure is reasonable because the planets all have very small masses compared with that of the
Sun, and also have relatively small orbital eccentricities and inclinations.
) to second order in the orbital eccentricities and inclinations. The nonsecular terms in the disturbing functions are
evaluated to first order in the
eccentricities and inclinations. (See Appendix H.) This expansion procedure is reasonable because the planets all have very small masses compared with that of the
Sun, and also have relatively small orbital eccentricities and inclinations.
There is an analogous set of equations, which can be derived from Equations (10.7) and (10.9), that describe the time evolution of the osculating orbital elements of the second planet due to the perturbing influence of the first. These take the form (see Section H.2)
where (see Section H.3) Here,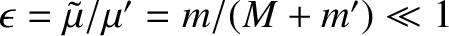 , and
, and
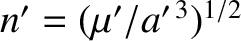 .
.