Next: Maxwell's Equations Up: Magnetic Induction Previous: Alternating Current Motors
Let us consider a particularly simple transformer in which the primary and secondary
coils are solenoids that share the same air-filled core. Suppose that
 is the length of the core, and
is the length of the core, and  is its cross-sectional area. Let
is its cross-sectional area. Let 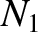 be
the total number of turns in the primary coil, and let
be
the total number of turns in the primary coil, and let  be the
total number of turns
in the secondary coil. Suppose that an alternating voltage
be the
total number of turns
in the secondary coil. Suppose that an alternating voltage
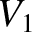 is the peak voltage in the primary circuit, and
is the peak voltage in the primary circuit, and  is the
alternation frequency (in radians per second). The current driven around the
primary circuit is written
where
is the
alternation frequency (in radians per second). The current driven around the
primary circuit is written
where 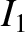 is the peak current. This current generates a
changing magnetic flux,
in the core of the solenoid, that links the secondary coil, and, thereby,
inductively generates the alternating emf
in the secondary circuit, where
is the peak current. This current generates a
changing magnetic flux,
in the core of the solenoid, that links the secondary coil, and, thereby,
inductively generates the alternating emf
in the secondary circuit, where  is the peak voltage. Suppose that this
emf drives an alternating current
around the secondary circuit, where
is the peak voltage. Suppose that this
emf drives an alternating current
around the secondary circuit, where 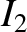 is the peak current.
is the peak current.
The circuit equation for the primary circuit is written
assuming that there is negligible resistance in this circuit. The first term in the previous equation is the externally generated emf. The second term is the back-emf due to the self inductance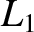 of the primary coil. (See Section 2.3.5.) The
final term is the emf due to the mutual inductance
of the primary coil. (See Section 2.3.5.) The
final term is the emf due to the mutual inductance  of the primary
and secondary coils. (See Section 2.3.7.) In the absence of any significant resistance in the primary
circuit, these three emfs must add up to zero. Equations (2.442)–(2.446) can be combined to give
because
of the primary
and secondary coils. (See Section 2.3.7.) In the absence of any significant resistance in the primary
circuit, these three emfs must add up to zero. Equations (2.442)–(2.446) can be combined to give
because
The alternating emf generated in the secondary circuit consists of the
emf generated by the self inductance,  , of the secondary coil, plus the
emf generated by the mutual inductance of the primary and secondary coils.
Thus,
, of the secondary coil, plus the
emf generated by the mutual inductance of the primary and secondary coils.
Thus,
Now, the instantaneous power output of the external AC power source that drives the primary circuit is
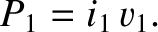 |
(2.451) |
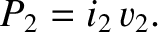 |
(2.452) |
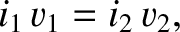 |
(2.453) |
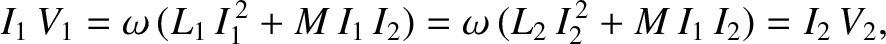 |
(2.455) |
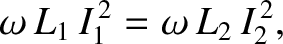 |
(2.456) |
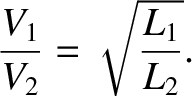 |
(2.458) |
Now, from Section 2.3.5, the self inductances of the primary and
secondary coils are given by
 and
and
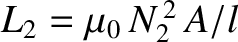 , respectively. It follows
that
, respectively. It follows
that
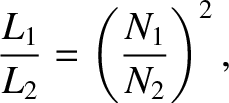 |
(2.459) |
AC electricity is generated in power stations at a fairly low peak voltage
(i.e., something like 440 V), and is consumed by the domestic
user at a peak voltage of 110 V (in the U.S.). However, AC electricity
is transmitted from the power station to the location where it is consumed
at a very high peak voltage (typically 50 kV). In fact, as soon as an AC signal
comes out of a generator in a power station it is fed into a step-up
transformer that boosts its peak voltage from a few hundred volts to many tens
of kilovolts. The output from the step-up transformer is fed into a
high tension transmission line, which typically transports the electricity over
many tens of kilometers, and, once the electricity has reached its
point of consumption, it is fed through a series of step-down transformers,
until, by the time it emerges from a domestic power socket, its peak voltage is
only 110 V. But, if AC electricity is both generated and consumed at
comparatively low peak voltages, why go to the trouble of
stepping up the peak voltage to a very high value at the
power station, and then stepping down the voltage again once the electricity
has reached its point of consumption? Why not generate, transmit, and
distribute the electricity at a peak voltage of 110 V?
Well, consider an electric
power line that transmits a peak electric power  between a power station
and a city. We can think of
between a power station
and a city. We can think of  , which
depends on the number of consumers in the city, and the nature of the
electrical devices that they operate, as essentially a fixed number.
Suppose that
, which
depends on the number of consumers in the city, and the nature of the
electrical devices that they operate, as essentially a fixed number.
Suppose that  and
and  are the peak voltage and peak current
of the AC signal transmitted along the transmission line,
respectively. We can think of these numbers as being variable, because we can change
them using a transformer. However, because
are the peak voltage and peak current
of the AC signal transmitted along the transmission line,
respectively. We can think of these numbers as being variable, because we can change
them using a transformer. However, because 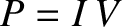 , the product of the peak
voltage and the peak current must remain constant. Suppose that the resistance
of the transmission line is
, the product of the peak
voltage and the peak current must remain constant. Suppose that the resistance
of the transmission line is  . The peak rate at which electrical energy is lost due
to ohmic heating in the line is
. The peak rate at which electrical energy is lost due
to ohmic heating in the line is
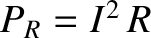 (see Section 2.1.11), which can be written
(see Section 2.1.11), which can be written
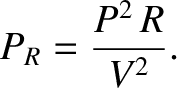 |
(2.461) |
 , transmitted down the line is a fixed quantity,
as is the resistance,
, transmitted down the line is a fixed quantity,
as is the resistance,  , of the line, then the
power lost in the line due to ohmic heating varies like the inverse square
of
the peak voltage in the line. It turns out that even at very high voltages,
such as 50 kV, the ohmic power losses in
transmission lines that run over tens of kilometers
can amount to up to 20% of the transmitted power. It can readily be
appreciated that if an attempt were made to transmit AC electric power
at a peak voltage of 110 V then the ohmic losses would be so severe that virtually none of
the power would reach its destination. Thus, it is only possible to generate
electric power at a central location, transmit it over long distances,
and then distribute it at its point of consumption, if the transmission
is performed at a very high peak voltages (in fact, the higher, the better). Transformers
play a vital role in this process because they allow us to step-up
and step-down the voltage of an AC electric signal
very efficiently (a well-designed
transformer typically has a power loss that is only a few percent of the
total power flowing through it).
, of the line, then the
power lost in the line due to ohmic heating varies like the inverse square
of
the peak voltage in the line. It turns out that even at very high voltages,
such as 50 kV, the ohmic power losses in
transmission lines that run over tens of kilometers
can amount to up to 20% of the transmitted power. It can readily be
appreciated that if an attempt were made to transmit AC electric power
at a peak voltage of 110 V then the ohmic losses would be so severe that virtually none of
the power would reach its destination. Thus, it is only possible to generate
electric power at a central location, transmit it over long distances,
and then distribute it at its point of consumption, if the transmission
is performed at a very high peak voltages (in fact, the higher, the better). Transformers
play a vital role in this process because they allow us to step-up
and step-down the voltage of an AC electric signal
very efficiently (a well-designed
transformer typically has a power loss that is only a few percent of the
total power flowing through it).
Of course, transformers do not work for direct current (DC) electricity, because the magnetic flux generated by the primary coil does not vary in time, and, therefore, does not induce an emf in the secondary coil. In fact, there is no efficient method of stepping-up or stepping-down the voltage of a DC electric signal. Thus, it is impossible to efficiently transmit DC electric power over long distances. This is the main reason why commercially generated electricity is AC, rather than DC.