Electric Scalar Potential
We now have a problem. We can only write the electric field in terms of a
scalar potential (i.e.,
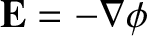 ) provided that
) provided that
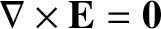 . This follows because
. This follows because
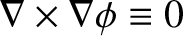 . (See Section A.22.) However, we have just discovered that the curl of the electric field is non-zero in the presence of a changing magnetic field.
In other words,
. (See Section A.22.) However, we have just discovered that the curl of the electric field is non-zero in the presence of a changing magnetic field.
In other words,  is not, in general, a conservative field. Does this
mean that we have to abandon the concept of electric scalar potential?
Fortunately, it does not. It is still possible to define a scalar potential that is
physically meaningful.
is not, in general, a conservative field. Does this
mean that we have to abandon the concept of electric scalar potential?
Fortunately, it does not. It is still possible to define a scalar potential that is
physically meaningful.
Let us start from the field equation
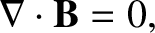 |
(2.293) |
which is valid for both time-varying and constant magnetic fields. Because the
magnetic field is solenoidal, we can write it as the curl of a vector potential:
 |
(2.294) |
[See Equation (2.251)]. This follows because
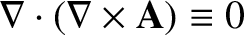 . (See Section A.22.)
So, there is no problem with the vector potential in the presence of time-varying fields. Let us substitute Equation (2.294) into the field equation (2.286).
We obtain
. (See Section A.22.)
So, there is no problem with the vector potential in the presence of time-varying fields. Let us substitute Equation (2.294) into the field equation (2.286).
We obtain
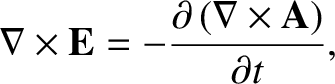 |
(2.295) |
which can be written
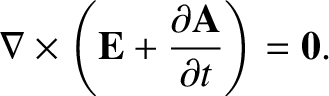 |
(2.296) |
Now, we know that a curl-free vector field can always be expressed as the gradient of
a scalar potential (see Section A.22), so let us write
 |
(2.297) |
or
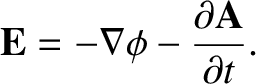 |
(2.298) |
This equation implies that the electric scalar potential,  , only
describes the conservative electric field generated by electric charges.
The electric field induced by time-varying magnetic fields is non-conservative, and
is described by the magnetic vector potential,
, only
describes the conservative electric field generated by electric charges.
The electric field induced by time-varying magnetic fields is non-conservative, and
is described by the magnetic vector potential, 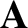 .
.
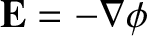 ) provided that
) provided that
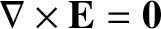 . This follows because
. This follows because
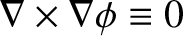 . (See Section A.22.) However, we have just discovered that the curl of the electric field is non-zero in the presence of a changing magnetic field.
In other words,
. (See Section A.22.) However, we have just discovered that the curl of the electric field is non-zero in the presence of a changing magnetic field.
In other words,  is not, in general, a conservative field. Does this
mean that we have to abandon the concept of electric scalar potential?
Fortunately, it does not. It is still possible to define a scalar potential that is
physically meaningful.
is not, in general, a conservative field. Does this
mean that we have to abandon the concept of electric scalar potential?
Fortunately, it does not. It is still possible to define a scalar potential that is
physically meaningful.
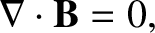
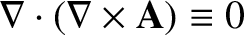 . (See Section A.22.)
So, there is no problem with the vector potential in the presence of time-varying fields. Let us substitute Equation (2.294) into the field equation (2.286).
We obtain
. (See Section A.22.)
So, there is no problem with the vector potential in the presence of time-varying fields. Let us substitute Equation (2.294) into the field equation (2.286).
We obtain
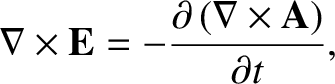
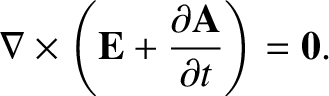

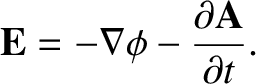
 , only
describes the conservative electric field generated by electric charges.
The electric field induced by time-varying magnetic fields is non-conservative, and
is described by the magnetic vector potential,
, only
describes the conservative electric field generated by electric charges.
The electric field induced by time-varying magnetic fields is non-conservative, and
is described by the magnetic vector potential, 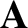 .
.