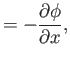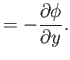Next: Subsonic Flow Past a
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Homenergic Homentropic Flow
Small-Perturbation Theory
A great number of problems of interest in compressible fluid mechanics are concerned with the perturbation of a known flow pattern. The most common case is that of
uniform, steady flow. Let 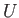 denote the uniform flow velocity, which is directed parallel to the
denote the uniform flow velocity, which is directed parallel to the  -axis. The density, pressure, and temperature
are also assumed to be uniform, and are denoted
-axis. The density, pressure, and temperature
are also assumed to be uniform, and are denoted
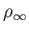 ,
, 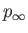 , and
, and 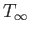 , respectively. The corresponding sound speed is
, respectively. The corresponding sound speed is
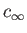 , and the Mach number is
, and the Mach number is
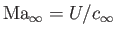 . Finally. the velocity field of the unperturbed flow pattern is
. Finally. the velocity field of the unperturbed flow pattern is
Suppose that a solid body, such as an airfoil, is placed in the aforementioned flow pattern. The cross-section of the body is assumed to
be independent of the Cartesian coordinate  . The body disturbs the flow pattern, and changes its velocity field,
which is now written
. The body disturbs the flow pattern, and changes its velocity field,
which is now written
where 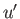 and
and 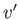 are known as induced velocity components. We are interested in situations in which
are known as induced velocity components. We are interested in situations in which 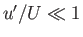 and
and 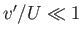 .
.
Equation (15.101) can be combined with the previous two equations to give
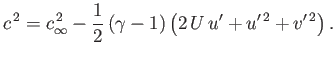 |
(15.106) |
It then follows from Equation (15.100) that
The previous equation is exact. However, if 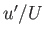 and
and 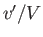 are small then it becomes possible to neglect many of the terms on the right-hand
side. For instance, neglecting terms that are third-order in small quantities, we obtain
are small then it becomes possible to neglect many of the terms on the right-hand
side. For instance, neglecting terms that are third-order in small quantities, we obtain
Furthermore, if we neglect terms that are second-order in small quantities then we get the linear equation
Note, however, than in so-called transonic flow, where
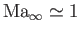 , the coefficient of
, the coefficient of
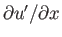 on the left-hand side of Equation (15.108) becomes very small. In this situation, it is not possible to neglect the
first term on the right-hand side. However, the condition
on the left-hand side of Equation (15.108) becomes very small. In this situation, it is not possible to neglect the
first term on the right-hand side. However, the condition
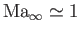 does not affect the
term
does not affect the
term
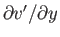 on the left-hand side of Equation (15.108), and so the other terms on the right-hand side can still be neglected. Thus, transonic
flow is governed by the non-linear equation
on the left-hand side of Equation (15.108), and so the other terms on the right-hand side can still be neglected. Thus, transonic
flow is governed by the non-linear equation
On the other hand, subsonic (i.e.,
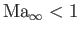 ) and supersonic flow (i.e.,
) and supersonic flow (i.e.,
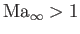 ) are both governed by Equation (15.109).
Another situation in which certain terms on the right-hand side of Equation (15.108) must be retained is hypersonic flow
(i.e.,
) are both governed by Equation (15.109).
Another situation in which certain terms on the right-hand side of Equation (15.108) must be retained is hypersonic flow
(i.e.,
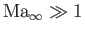 ). This follows because, although
). This follows because, although 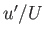 and
and 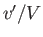 are small, their products with
are small, their products with
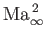 can
still be non-negligible. Roughly speaking, Equation (15.109) is valid for
can
still be non-negligible. Roughly speaking, Equation (15.109) is valid for
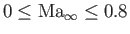 and
and
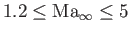 .
In other words, transonic flow corresponds to
.
In other words, transonic flow corresponds to
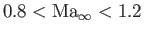 , and hypersonic flow to
, and hypersonic flow to
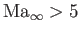 (Anderson 2003).
(Anderson 2003).
The pressure coefficient is
defined
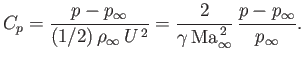 |
(15.111) |
(See Section 15.9.)
Equation (15.101) implies that
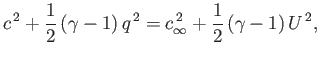 |
(15.112) |
where
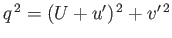 . Moreover, Equation (14.61) yields
. Moreover, Equation (14.61) yields
![$\displaystyle \frac{p}{p_\infty} = \left[\frac{2+(\gamma-1)\,{\rm Ma}_\infty^{\,2}}{2+(\gamma-1)\,{\rm Ma}^{\,2}}\right]^{\,\gamma/(\gamma-1)},$](img5927.png) |
(15.113) |
where
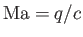 . The previous two equations can be combined to give
. The previous two equations can be combined to give
![$\displaystyle \frac{p}{p_\infty} = \left[1+\frac{1}{2}\,(\gamma-1)\,{\rm Ma}_\infty^{\,2}\left(1-\frac{q^{\,2}}{U^{\,2}}\right)\right]^{\,\gamma/(\gamma-1)}.$](img5929.png) |
(15.114) |
Hence, we obtain
![$\displaystyle C_p = \frac{2}{\gamma\,{\rm Ma}_\infty^{\,2}}\left(\left[1+\frac{...
...2}\left(1-\frac{q^{\,2}}{U^{\,2}}\right)\right]^{\,\gamma/(\gamma-1)}-1\right),$](img5930.png) |
(15.115) |
which reduces to
![$\displaystyle C_p = \frac{2}{\gamma\,{\rm Ma}_\infty^{\,2}}\left(\left[1-\frac{...
...\frac{u'^{\,2}+v'^{\,2}}{U^{\,2}}\right)\right]^{\,\gamma/(\gamma-1)}-1\right).$](img5931.png) |
(15.116) |
Using the binomial expansion on the expression in square brackets, and neglecting terms that are third-order, or higher, in small quantities, we obtain
![$\displaystyle C_p \simeq -\left[\frac{2\,u'}{U}+(1-{\rm Ma}_\infty^{\,2})\left(\frac{u'}{U}\right)^{\,2}+ \left(\frac{v'}{U}\right)^2\right].$](img5932.png) |
(15.117) |
For two-dimensional flows, in the limit in which Equation (15.109) is valid, it is consistent to retain only
first-order terms in the previous equation, so that
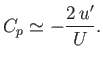 |
(15.118) |
Let
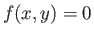 |
(15.119) |
be
the equation of the surface of the solid body that perturbs the flow. At the surface, the velocity vector of the flow must be perpendicular
to the local normal: that is, the flow must be tangential to the surface. In other words,
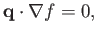 |
(15.120) |
which reduces to
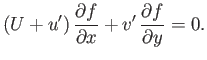 |
(15.121) |
Neglecting 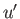 with respect to
with respect to 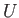 , we obtain
, we obtain
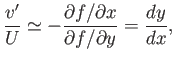 |
(15.122) |
where 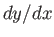 is the slope of the surface, and
is the slope of the surface, and 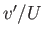 the approximate slope of a streamline.
the approximate slope of a streamline.
Now, the body has to be thin in order to satisfy our assumption that the induced velocities are relatively small.
This implies that the coordinate  differs little from zero (say) on the surface of the body. Hence, we can write
differs little from zero (say) on the surface of the body. Hence, we can write
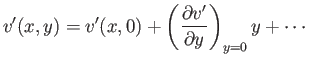 |
(15.123) |
in the immediate vicinity of the surface. Within the framework of small-perturbation theory, it is consistent to neglect all
terms on the right-hand side of the previous equation after the first. Hence, the boundary condition
(15.122) reduces to
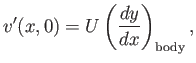 |
(15.124) |
respectively.
Because a homenergic, homentropic flow pattern is necessarily irrotational (see Section 15.10), we can write
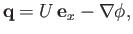 |
(15.125) |
where 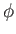 is the perturbed velocity potential. (See Section 4.15.) It follows that
is the perturbed velocity potential. (See Section 4.15.) It follows that
Hence, Equations (15.109), (15.118), and (15.124) become
respectively.



Next: Subsonic Flow Past a
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Homenergic Homentropic Flow
Richard Fitzpatrick
2016-03-31
![]() . The body disturbs the flow pattern, and changes its velocity field,
which is now written
. The body disturbs the flow pattern, and changes its velocity field,
which is now written
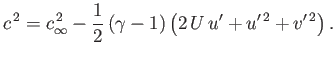
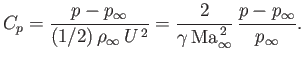
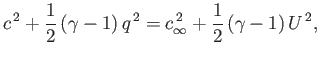
![$\displaystyle \frac{p}{p_\infty} = \left[\frac{2+(\gamma-1)\,{\rm Ma}_\infty^{\,2}}{2+(\gamma-1)\,{\rm Ma}^{\,2}}\right]^{\,\gamma/(\gamma-1)},$](img5927.png)
![$\displaystyle \frac{p}{p_\infty} = \left[1+\frac{1}{2}\,(\gamma-1)\,{\rm Ma}_\infty^{\,2}\left(1-\frac{q^{\,2}}{U^{\,2}}\right)\right]^{\,\gamma/(\gamma-1)}.$](img5929.png)
![$\displaystyle C_p = \frac{2}{\gamma\,{\rm Ma}_\infty^{\,2}}\left(\left[1+\frac{...
...2}\left(1-\frac{q^{\,2}}{U^{\,2}}\right)\right]^{\,\gamma/(\gamma-1)}-1\right),$](img5930.png)
![$\displaystyle C_p \simeq -\left[\frac{2\,u'}{U}+(1-{\rm Ma}_\infty^{\,2})\left(\frac{u'}{U}\right)^{\,2}+ \left(\frac{v'}{U}\right)^2\right].$](img5932.png)
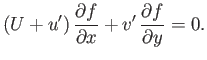
![]() differs little from zero (say) on the surface of the body. Hence, we can write
differs little from zero (say) on the surface of the body. Hence, we can write