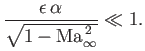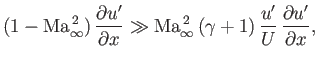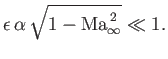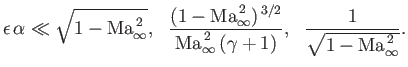Next: Supersonic Flow Past a
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Small-Perturbation Theory
Subsonic Flow Past a Wave-Shaped Wall
The following simple example serves to clarify many of the concepts introduced in the previous section. Consider
flow past a straight wall with a small-amplitude sinusoidal modulation whose surface is specified by
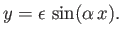 |
(15.130) |
Here,  is the amplitude of the modulation, whereas
is the amplitude of the modulation, whereas
 is the wavelength.
In the limit
is the wavelength.
In the limit
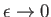 , the unperturbed flow is of uniform speed
, the unperturbed flow is of uniform speed 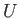 , directed parallel to the
, directed parallel to the  -axis.
The corresponding Mach number is
-axis.
The corresponding Mach number is
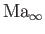 . The fluid occupies the region
. The fluid occupies the region
 .
.
The perturbed flow is governed by Equation (15.127),
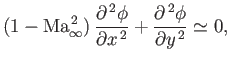 |
(15.131) |
and is subject to the boundary condition (15.129), which can be written
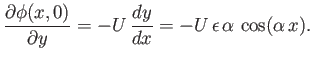 |
(15.132) |
We also expect the perturbed flow to become vanishingly small far from the wall, which implies that
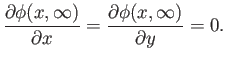 |
(15.133) |
Consider subsonic flow, for which
 .
Equation (15.131) is of the elliptic type
.
Equation (15.131) is of the elliptic type
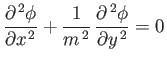 |
(15.134) |
(Arfken 1985). Let us search for a separable solution of the form
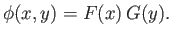 |
(15.135) |
We obtain
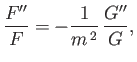 |
(15.136) |
where  denotes derivative with respect to argument.
Given that the left-hand side of the previous equation is a function of
denotes derivative with respect to argument.
Given that the left-hand side of the previous equation is a function of  only, whereas the right-hand side is
a function of
only, whereas the right-hand side is
a function of  only, the two sides must equal the same constant. In other words,
only, the two sides must equal the same constant. In other words,
Here, the sign of the constant has been chosen so as to allow the boundary condition (15.133) to be satisfied.
The most general solution of Equation (15.137)
is
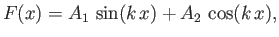 |
(15.139) |
where 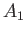 and
and 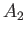 are arbitrary constants. Likewise, the most general solution of Equation (15.138)
is
are arbitrary constants. Likewise, the most general solution of Equation (15.138)
is
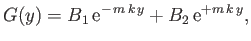 |
(15.140) |
where 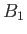 and
and 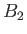 are arbitrary constants.
are arbitrary constants.
The boundary condition (15.133) implies that  . The boundary condition (15.132) then yields
. The boundary condition (15.132) then yields
![$\displaystyle -m\,k\,B_1\left[A_1\,\sin(k\,x) +A_2\,\cos(k\,x)\right] = -U\,\epsilon\,\alpha\,\cos(\alpha\,x).$](img5971.png) |
(15.141) |
This condition can only be satisfied at all  if
if 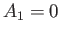 ,
, 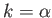 , and
, and
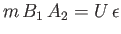 .
Thus, we obtain
.
Thus, we obtain
According to Equation (15.128), the pressure coefficient at the wall can be written
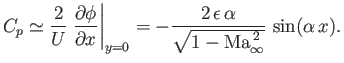 |
(15.145) |
It immediately follows that there is zero net drag force acting on the wall, because the pressure variations are in phase with the wall's sinusoidal modulations, and, hence, symmetrical
about the crests and troughs.
Let us now consider under what circumstances the approximations made in the small-perturbation theory developed in the previous section
are valid for the problem under investigation. In fact, small-perturbation theory is premised on three assumptions. First,
that 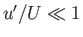 and
and 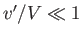 . It is evident from Equations (15.143) and (15.144) that this assumption is valid
provided
. It is evident from Equations (15.143) and (15.144) that this assumption is valid
provided
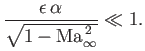 |
(15.146) |
Second, in Equation (15.110) it is assumed that
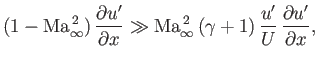 |
(15.147) |
which implies that
 |
(15.148) |
Finally, in Equation (15.123), it is assumed that the second term on the right-hand side is negligible compared to the
first, when evaluated at the surface of the wall, which implies that
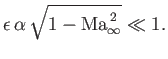 |
(15.149) |
Hence, we deduce that the analysis described in this section is valid provided
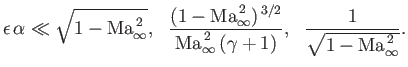 |
(15.150) |



Next: Supersonic Flow Past a
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Small-Perturbation Theory
Richard Fitzpatrick
2016-03-31
![]() .
Equation (15.131) is of the elliptic type
.
Equation (15.131) is of the elliptic type
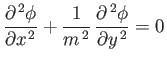
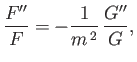
![]() . The boundary condition (15.132) then yields
. The boundary condition (15.132) then yields
![]() and
and ![]() . It is evident from Equations (15.143) and (15.144) that this assumption is valid
provided
. It is evident from Equations (15.143) and (15.144) that this assumption is valid
provided