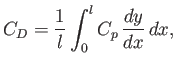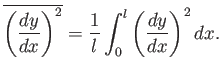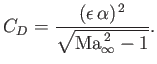Next: Linearized Subsonic Flow
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Subsonic Flow Past a
Supersonic Flow Past a Wave-Shaped Wall
Suppose that the unperturbed flow in the problem considered in the previous section is supersonic, so that
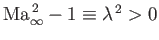 . The perturbed flow is governed by Equation (15.127), which is now
of the hyperbolic type
. The perturbed flow is governed by Equation (15.127), which is now
of the hyperbolic type
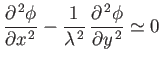 |
(15.151) |
(Arfken 1985). As is easily verified, the previous equation has the general solution
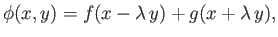 |
(15.152) |
where 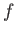 and
and 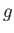 are arbitrary functions (Fitzpatrick 2013). It is clear that
are arbitrary functions (Fitzpatrick 2013). It is clear that 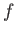 is constant along lines
is constant along lines
 , whereas
, whereas
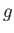 is constant along lines
is constant along lines
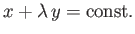 . These lines are inclined at the Mach angle,
. These lines are inclined at the Mach angle,
![$ \mu=\cot^{-1}[({\rm Ma}_\infty^{\,2}-1)^{\,1/2}]$](img5990.png) ,
to the undisturbed flow. They are, in fact, the Mach lines, or characteristics, of the unperturbed flow. (See Section 15.3.)
The former characteristics are inclined downstream. In other words, they originate at the wall.
The latter characteristics are inclined upstream. In other words, they originate at infinity. Because there are no sources at
infinity, the latter characteristics carry no perturbation, which implies that
,
to the undisturbed flow. They are, in fact, the Mach lines, or characteristics, of the unperturbed flow. (See Section 15.3.)
The former characteristics are inclined downstream. In other words, they originate at the wall.
The latter characteristics are inclined upstream. In other words, they originate at infinity. Because there are no sources at
infinity, the latter characteristics carry no perturbation, which implies that 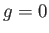 .
.
The boundary condition at the wall, (15.129), yields
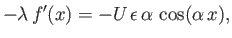 |
(15.153) |
where  denotes derivative with respect to argument. It follows that
denotes derivative with respect to argument. It follows that
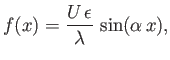 |
(15.154) |
and, hence, that
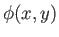 |
![$\displaystyle = f(x-\lambda\,y) = \frac{U\,\epsilon}{\lambda}\,\sin[\alpha\,(x-\lambda\,y)],$](img5994.png) |
(15.155) |
 |
![$\displaystyle =-\frac{\partial\phi}{\partial x} = -\frac{U\,\epsilon\,\alpha}{\lambda}\,\cos[\alpha\,(x-\lambda\,y)],$](img5995.png) |
(15.156) |
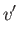 |
![$\displaystyle =- \frac{\partial\phi}{\partial y}=U\,\epsilon\,\alpha\,\cos[\alpha\,(x-\lambda\,y)].$](img5996.png) |
(15.157) |
Note that, unlike the case of subsonic flow, the amplitude of the perturbed velocity does not decrease with increasing distance from
the wall.
The pressure coefficient at the wall is
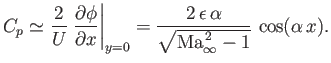 |
(15.158) |
It can be seen, by comparison with Equation (15.145), that the maxima and minima of the pressure
are now phase-shifted by 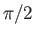 radians with respect to the corresponding maxima and minima in the subsonic
case. Hence, the pressure distribution at the wall is anti-symmetric with respect to the crests and troughs of the wall.
Consequently, a net drag force is exerted on the wall.
The mean coefficient of drag per wavelength is [see Equation (15.56)]
radians with respect to the corresponding maxima and minima in the subsonic
case. Hence, the pressure distribution at the wall is anti-symmetric with respect to the crests and troughs of the wall.
Consequently, a net drag force is exerted on the wall.
The mean coefficient of drag per wavelength is [see Equation (15.56)]
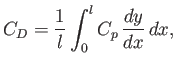 |
(15.159) |
which is obtained by replacing the sine of the slope of the wall by the tangent,  . This approximation is valid within the
context of the small-perturbation theory.
However, according to Equations (15.130) and (15.158),
. This approximation is valid within the
context of the small-perturbation theory.
However, according to Equations (15.130) and (15.158), 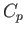 can be written
can be written
 |
(15.160) |
which implies that
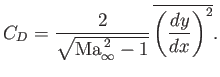 |
(15.161) |
Here, the bar denotes a period average of the form
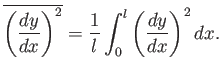 |
(15.162) |
Equations (15.160) and (15.161) are valid for any small-amplitude, periodic modulation of the wall.
For the particular sinusoidal modulation under consideration in this section, we find that
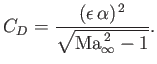 |
(15.163) |
The discussion of the range of validity of the approximations used in deriving the previous results follows the same lines
as in the subsonic case.



Next: Linearized Subsonic Flow
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Subsonic Flow Past a
Richard Fitzpatrick
2016-03-31
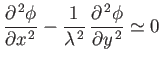
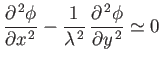
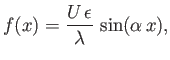
![$\displaystyle = f(x-\lambda\,y) = \frac{U\,\epsilon}{\lambda}\,\sin[\alpha\,(x-\lambda\,y)],$](img5994.png)
![$\displaystyle =-\frac{\partial\phi}{\partial x} = -\frac{U\,\epsilon\,\alpha}{\lambda}\,\cos[\alpha\,(x-\lambda\,y)],$](img5995.png)
![$\displaystyle =- \frac{\partial\phi}{\partial y}=U\,\epsilon\,\alpha\,\cos[\alpha\,(x-\lambda\,y)].$](img5996.png)